Maison >développement back-end >Tutoriel C#.Net >Auto-apprentissage C#07 à partir de 0 - File d'attente en spirale et mouvement en spirale
Auto-apprentissage C#07 à partir de 0 - File d'attente en spirale et mouvement en spirale
- 黄舟original
- 2017-02-04 10:46:121842parcourir
Réalisation d'un mouvement en spirale basé sur la logique de file d'attente en spirale
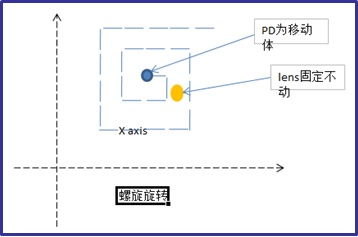
La méthode inverse de l'algorithme de file d'attente en spirale contrôle le moteur à deux axes pour qu'il se déplace le long d'une trajectoire en spirale, comme le montre la figure ci-dessous.
1. Analyse de l'algorithme de file d'attente en spirale
La figure suivante est une file d'attente en spirale. Supposons que les coordonnées de 1 sont (0, 0), que la direction x est positive vers la droite et que la direction y est positive vers le bas. Par exemple, les coordonnées de 7 sont (-1, -1) et les coordonnées de. 2 sont (1, 0). La programmation vous permet de saisir les coordonnées (x, y) de n'importe quel point et de sortir le numéro correspondant ! (Republié depuis Internet)
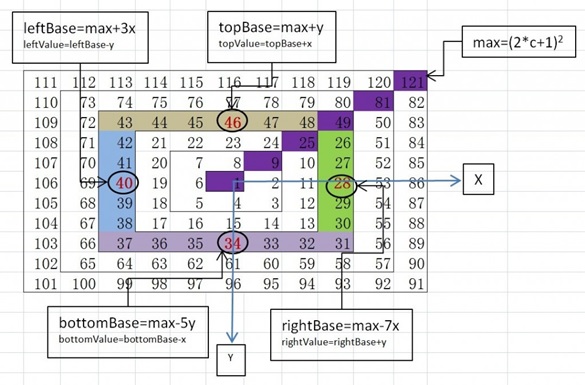
La valeur maximale par cercle max=(2*c 1)(2*c 1), c'est la raison Le nombre de tours de l'intérieur vers l'extérieur.
Les différences entre ces valeurs de référence et max sont 1C (en haut), 3C (à gauche), 5C (en bas), 7C (à droite) (C représente le numéro du tour actuel), en haut et en bas , y La coordonnée représente (ou est égale à) le nombre de cercles (c'est-à-dire C=y), tandis qu'à gauche et à droite la coordonnée x représente (ou est égale à) le nombre de cercles (c'est-à-dire C=x). Par conséquent, la différence mentionnée précédemment peut être exprimée sous la forme 1y, 3x, 5y, 7x en utilisant les coordonnées.
Implémentation du code :
private static Object spiral(int x, int y)
{
int c = max(abs(x), abs(y));// 当前坐标所在圈
int max = (c * 2 + 1) * (c * 2 + 1);// 当前圈上最大值
if (y == -c) { // 上边
return max + (x + y);
} else if (x == -c) {// 左边
return max + (3 * x - y);
} else if (y == c) {// 下边
return max + (-x - 5 * y);
} else {// 右边
return max + (-7 * x + y);
}
}2. Mouvement en spirale
Personnalisez d'abord l'opération de coordonnées pour représenter la position logique de PD.
struct Coordinate
{ public int X; public int Y; public Coordinate(int a, int b)
{
X = a;
Y = b;
} public static bool operator ==(Coordinate loc1, Coordinate loc2)
{ return (loc1.X == loc2.X) && (loc1.Y == loc2.Y);
} public static bool operator !=(Coordinate loc1, Coordinate loc2)
{ return !(loc1 == loc2);
} public override bool Equals(object loc)
{ return this == (Coordinate)loc;
} public override int GetHashCode()
{ return base.GetHashCode();
} public static Coordinate operator -(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X - loc2.X, loc1.Y - loc2.Y);
} public static Coordinate operator +(Coordinate loc1, Coordinate loc2)
{ return new Coordinate(loc1.X + loc2.X, loc1.Y + loc2.Y);
} public override string ToString()
{ return "(" + X + "," + Y + ")";
}
}Utilisez ensuite la méthode inverse pour calculer les coordonnées x et y en fonction du nombre d'étapes.
public Coordinate ToLocation(int step, int pulse)
{
int c = (int)Math.Ceiling((Math.Sqrt(step) - 1) / 2);
int max = (int)Math.Pow(2 * c + 1, 2);
int x, y;
y = -c;//top
x = -(max + y - step);
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = -c;//left
y = max + 3 * x - step;
if (Math.Abs(y) <= Math.Abs(x))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
y = c;//bottom
x = max - 5 * y - step;
if (Math.Abs(x) <= Math.Abs(y))
{
this.location.X = x * pulse;
this.location.Y = y * pulse;
return this.location;
}
x = c;//right
y = -(max - 7 * x - step);
this.location.X = x * pulse;
this.location.Y = y * pulse;
//LocChange();
return this.location;
}Enfin, le mouvement se réalise en fonction du changement de coordonnées.
public void Start()
{
Coordinate moveToLoc, currentLoc, deltaLoc;
currentLoc = ToLocation(1, 0);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the start location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "begin to move... ");
log.SaveLogToTxt(logInfo);
for (int step = 1; step <= this.roMaxStep[0]; step++)
{
moveToLoc = ToLocation(step + 1, this.roPulse[0]);
deltaLoc = moveToLoc - currentLoc;
logInfo = string.Format("{0}: step{1}{2}{3}...", DateTime.Now.ToString("HH:mm:ss"), step + " ", "move to ", moveToLoc.ToString());
log.SaveLogToTxt(logInfo);
bool moveX = card.MoveX(deltaLoc.X);
bool moveY = card.MoveY(deltaLoc.Y);
if (moveX == false || moveY == false)
//throw error
return;
currentLoc = moveToLoc;
//if RES > RoRESTarget
//break;
}
logInfo = string.Format("{0}: {1}.", DateTime.Now.ToString("HH:mm:ss"), "move done");
log.SaveLogToTxt(logInfo);
logInfo = string.Format("{0}: {1}{2}.", DateTime.Now.ToString("HH:mm:ss"), "the current location is ", currentLoc.ToString());
log.SaveLogToTxt(logInfo);
}Ce qui précède est le contenu de l'auto-apprentissage C#07 de 0-Spiral Queue et Spiral Movement. Pour plus de contenu connexe, veuillez prêter attention au site Web PHP chinois (www.php.cn). !

