Analyse du principe de mise en œuvre de Java8 HashMap

La structure de stockage de HashMap est celle indiquée sur la figure : s'il y a plus de 8 nœuds dans un bucket, la structure de stockage est un arbre rouge-noir, et s'il y a moins de 8 nœuds, c'est un seul. façon liste chaînée.

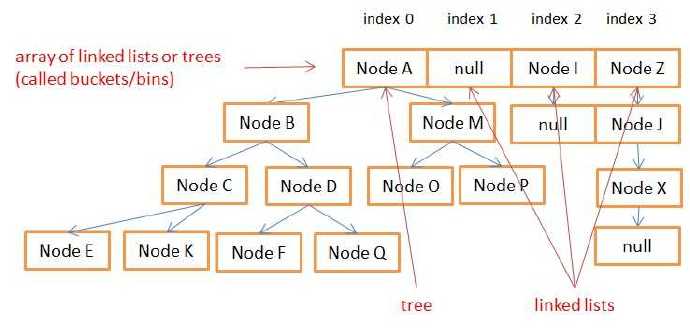
1 : Quelques propriétés de HashMap

public class HashMap<k,v> extends AbstractMap<k,v> implements Map<k,v>, Cloneable, Serializable {
private static final long serialVersionUID = 362498820763181265L;
// 默认的初始容量是16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
// 默认的填充因子(以前的版本也有叫加载因子的)
static final float DEFAULT_LOAD_FACTOR = 0.75f;
// 这是一个阈值，当桶(bucket)上的链表数大于这个值时会转成红黑树，put方法的代码里有用到
static final int TREEIFY_THRESHOLD = 8;
// 也是阈值同上一个相反，当桶(bucket)上的链表数小于这个值时树转链表
static final int UNTREEIFY_THRESHOLD = 6;
// 看源码注释里说是：树的最小的容量，至少是 4 x TREEIFY_THRESHOLD = 32 然后为了避免(resizing 和 treeification thresholds) 设置成64
static final int MIN_TREEIFY_CAPACITY = 64;
// 存储元素的数组，总是2的倍数
transient Node<k,v>[] table;
transient Set<map.entry<k,v>> entrySet;
// 存放元素的个数，注意这个不等于数组的长度。
transient int size;
// 每次扩容和更改map结构的计数器
transient int modCount;
// 临界值 当实际大小(容量*填充因子)超过临界值时，会进行扩容
int threshold;
// 填充因子
final float loadFactor;

2 : Méthode de construction de HashMap

// 指定初始容量和填充因子的构造方法
public HashMap(int initialCapacity, float loadFactor) {
// 指定的初始容量非负
if (initialCapacity < 0)
throw new IllegalArgumentException(Illegal initial capacity: +
initialCapacity);
// 如果指定的初始容量大于最大容量,置为最大容量
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
// 填充比为正
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException(Illegal load factor: +
loadFactor);
this.loadFactor = loadFactor;
// 指定容量后，tableSizeFor方法计算出临界值，put数据的时候如果超出该值就会扩容，该值肯定也是2的倍数
// 指定的初始容量没有保存下来，只用来生成了一个临界值
this.threshold = tableSizeFor(initialCapacity);
}
// 该方法保证总是返回大于cap并且是2的倍数的值，比如传入999 返回1024
static final int tableSizeFor(int cap) {
int n = cap - 1;
// 向右做无符号位移
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
// 三目运算符的嵌套
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
//构造函数2
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
//构造函数3
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}

3 : Déterminer la position de l'élément dans le tableau lors de l'obtention et de la mise

static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

Pour déterminer l'emplacement

La première étape consiste à calculer le code de hachage de la clé, qui est un numéro de type int. Les commentaires suivants sur le code source h >> 16 indiquent : Afin d'éviter les collisions de hachage (collisons de hachage), les bits élevés sont dispersés vers les bits faibles. Ceci est effectué après un examen approfondi de divers facteurs tels que la vitesse et les performances. .

Étape 2 : h est le code de hachage, length est la longueur du tableau Node[] ci-dessus et effectuez l'opération AND h & (length-1). Puisque la longueur est un multiple de 2 -1, son code binaire est entièrement 1, et le résultat de 1 et des autres nombres ci-dessus peut être 0 ou 1, garantissant ainsi l'uniformité après l'opération. C'est-à-dire que la méthode de hachage garantit l'uniformité des résultats, ce qui est très important et affectera grandement les performances put et get de HashMap. Regardez la comparaison ci-dessous :

La figure 3.1 est le résultat du hachage asymétrique

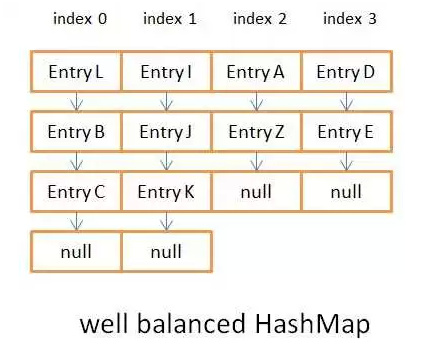
La figure 3.2 est le résultat du hachage équilibré

Il n'y a pas beaucoup de données dans ces deux images. Si la longueur de la liste chaînée dépasse 8, elle sera convertie en un arbre rouge-noir. Ce sera plus évident à ce moment-là. Avant jdk8, il s'agissait toujours d'une liste chaînée. La complexité de la requête de liste chaînée est O(n), tandis que la complexité de la requête de l'arbre rouge-noir est O(log(n)). à ses propres caractéristiques. Si les résultats de hachage sont inégaux, cela affectera grandement la complexité de l'opération. Les connaissances connexes ici sont72e1214e15ec42bfc5f5aa5e4f182c03Blog des connaissances de base de l'arbre rouge-noir5db79b134e9f6b82c0b36e0489ee08edIl existe également un exemple sur Internet Pour vérifier : personnalisez un objet comme clé, ajustez la méthode hashCode() pour voir combien de temps il faut pour mettre

public class MutableKeyTest {
public static void main(String args[]){
class MyKey {
Integer i;
public void setI(Integer i) {
this.i = i;
}
public MyKey(Integer i) {
this.i = i;
}
@Override
public int hashCode() {
// 如果返回1
// return 1
return i;
}
// object作为key存map里，必须实现equals方法
@Override
public boolean equals(Object obj) {
if (obj instanceof MyKey) {
return i.equals(((MyKey)obj).i);
} else {
return false;
}
}
}
// 我机器配置不高，25000的话正常情况27毫秒，可以用2500万试试，如果hashCode()方法返回1的话，250万就卡死
Map<MyKey,String> map = new HashMap<>(25000,1);
Date begin = new Date();
for (int i = 0; i < 20000; i++){
map.put(new MyKey(i), "test " + i);
}
Date end = new Date();
System.out.println("时间(ms) " + (end.getTime() - begin.getTime()));

4 : méthode get

public V get(Object key) {
Node<k,v> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<k,v> getNode(int hash, Object key) {
Node<k,v>[] tab; Node<k,v> first, e; int n; K k;
// hash & (length-1)得到红黑树的树根位置或者是链表的表头
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// 如果是树，遍历红黑树复杂度是O(log(n))，得到节点值
if (first instanceof TreeNode)
return ((TreeNode<k,v>)first).getTreeNode(hash, key);
// else是链表结构
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}

5 : méthode de mise, lors de la mise, localiser le seau selon h & (longueur – 1) puis vérifier s'il s'agit d'un rouge-noir arbre ou une liste chaînée puis putVal

public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<k,v>[] tab; Node<k,v> p; int n, i;
// 如果tab为空或长度为0，则分配内存resize()
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// (n - 1) & hash找到put位置，如果为空,则直接put
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<k,v> e; K k;
// 第一节节点hash值同，且key值与插入key相同
if (p.hash == hash &&((k = p.key) == key || (key != null && key.equals(k))))
e = p;
else if (p instanceof TreeNode)
// 红黑树的put方法比较复杂，putVal之后还要遍历整个树，必要的时候修改值来保证红黑树的特点
e = ((TreeNode<k,v>)p).putTreeVal(this, tab, hash, key, value);
else {
// 链表
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
// e为空，表示已到表尾也没有找到key值相同节点，则新建节点
p.next = newNode(hash, key, value, null);
// 新增节点后如果节点个数到达阈值，则将链表转换为红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
// 容许空key空value
if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 更新hash值和key值均相同的节点Value值
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}

6 : méthode de redimensionnement

final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 这一句比较重要，可以看出每次扩容是2倍
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}

Ce ci-dessus est l'éditeur. J'aimerais vous présenter les connaissances pertinentes sur l'analyse du principe d'implémentation de Java8 HashMap. J'espère que cela vous sera utile !

Pour plus d'articles liés à l'analyse des principes d'implémentation de Java8 HashMap, veuillez faire attention au site Web PHP chinois !