Maison >développement back-end >tutoriel php >解析PHP无限级分类方法及代码_PHP教程
解析PHP无限级分类方法及代码_PHP教程
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBoriginal
- 2016-07-21 15:04:00900parcourir
无论你要构建自己的论坛,在你的网站上发布消息还是书写自己的CMS程序,你都会遇到要在数据库中存储层次数据的情况。同时,除非你使用一种像XML的数据库,否则关系数据库中的表都不是层次结构的,他们只是一个平坦的列表。所以你必须找到一种把层次数据库转化的方法。
存储树形结构是一个很常见的问题,他有好几种解决方案。主要有两种方法:邻接列表模型和改进前序遍历树算法
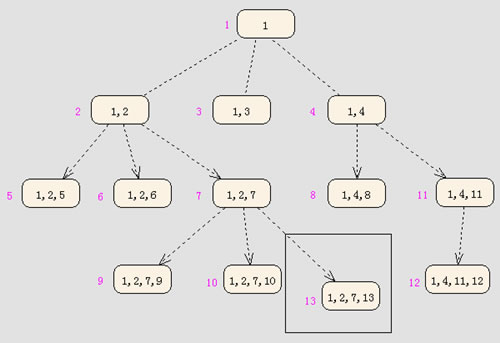
在本文中,我们将探讨这两种保存层次数据的方法。我将举一个在线食品店树形图的例子。这个食品店通过类别、颜色和品种来组织食品。树形图如下:
 本文包含了一些代码的例子来演示如何保存和获取数据。我选择PHP来写例子,因为我常用这个语言,而且很多人也都使用或者知道这个语言。你可以很方便地把它们翻译成你自己用的语言。
本文包含了一些代码的例子来演示如何保存和获取数据。我选择PHP来写例子,因为我常用这个语言,而且很多人也都使用或者知道这个语言。你可以很方便地把它们翻译成你自己用的语言。
我们要尝试的第一个——也是最优美的——方法称为“邻接列表模型”或称为“递归方法”。它是一个很优雅的方法因为你只需要一个简单的方法来在你的树中进行迭代。在我们的食品店中,邻接列表的表格如下:

如你所见,对每个节点保存一个“父”节点。我们可以看到“Pear”是“Green”的一个子节点,而后者又是“Fruit”的子节点,如此类推。 根节点,“Food”,则他的父节点没有值。为了简单,我只用了“title”值来标识每个节点。当然,在实际的数据库中,你要使用数字的ID。
显示树
现在我们已经把树放入数据库中了,得写一个显示函数了。这个函数将从根节点开始——没有父节点的节点——同时要显示这个节点所有的子节点。对于这些子节点,函数也要获取并显示这个子节点的子节点。然后,对于他们的子节点,函数还要再显示所有的子节点,然后依次类推。
也许你已经注意到了,这种函数的描述,有一种普遍的模式。我们可以简单地只写一个函数,用来获得特定节点的子节点。这个函数然后要对每个子节点调用自身来再次显示他们的子节点。这就是“递归”机制,因此称这种方法叫“递归方法”。
 要实现整个树,我们只要调用函数时用一个空字符串作为 $parent 和 $level = 0: display_children('',0); 函数返回了我们的食品店的树状图如下:
要实现整个树,我们只要调用函数时用一个空字符串作为 $parent 和 $level = 0: display_children('',0); 函数返回了我们的食品店的树状图如下:
Food
Fruit
Red
Cherry
Yellow
Banana
Meat
Beef
Pork
注意如果你只想看一个子树,你可以告诉函数从另一个节点开始。例如,要显示“Fruit”子树,你只要display_children('Fruit',0);
The Path to a Node节点的路径
利用差不多的函数,我们也可以查询某个节点的路径如果你只知道这个节点的名字或者ID。例如,“Cherry”的路径是“Food”> “Fruit”>“Red”。要获得这个路径,我们的函数要获得这个路径,这个函数必须从最深的层次开始:“Cheery”。但后查找这个节点的父 节点,并添加到路径中。在我们的例子中,这个父节点是“Red”。如果我们知道“Red”是“Cherry”的父节点。

这个函数现在返回了指定节点的路径。他把路径作为数组返回,这样我们可以使用print_r(get_path('Cherry')); 来显示,其结果是:
Array
(
[0] => Food
[1] => Fruit
[2] => Red)
不足
正如我们所见,这确实是一个很好的方法。他很容易理解,同时代码也很简单。但是邻接列表模型的缺点在哪里呢?在大多数编程语言中,他运行很慢,效率很差。这主要是“递归”造成的。我们每次查询节点都要访问数据库。
每次数据库查询都要花费一些时间,这让函数处理庞大的树时会十分慢。
造成这个函数不是太快的第二个原因可能是你使用的语言。不像Lisp这类语言,大多数语言不是针对递归函数设计的。对于每个节点,函数都要调用他自 己,产生新的实例。这样,对于一个4层的树,你可能同时要运行4个函数副本。对于每个函数都要占用一块内存并且需要一定的时间初始化,这样处理大树时递归 就很慢了。
改进前序遍历树现在,让我们看另一种存储树的方法。递归可能会很慢,所以我们就尽量不使用递归函数。我们也想尽量减少数据库查询的次数。最好是每次只需要查询一次。
我们先把树按照水平方式摆开。从根节点开始(“Food”),然后他的左边写上1。然后按照树的顺序(从上到下)给“Fruit”的左边写上2。这 样,你沿着树的边界走啊走(这就是“遍历”),然后同时在每个节点的左边和右边写上数字。最后,我们回到了根节点“Food”在右边写上18。下面是标上 了数字的树,同时把遍历的顺序用箭头标出来了。

我们称这些数字为左值和右值(如,“Food”的左值是1,右值是18)。正如你所见,这些数字按时了每个节点之间的关系。因为“Red”有3和6 两个值,所以,它是有拥有1-18值的“Food”节点的后续。同样的,我们可以推断所有左值大于2并且右值小于11的节点,都是有2-11的 “Food”节点的后续。这样,树的结构就通过左值和右值储存下来了。这种数遍整棵树算节点的方法叫做“改进前序遍历树”算法。
在继续前,我们先看看我们的表格里的这些值:

注意单词“left”和“right”在SQL中有特殊的含义。因此,我们只能用“lft”和“rgt”来表示这两个列。(译注——其实Mysql 中可以用“`”来表示,如“`left`”,MSSQL中可以用“[]”括出,如“[left]”,这样就不会和关键词冲突了。)同样注意这里我们已经不需要“parent”列了。我们只需要使用lft和rgt就可以存储树的结构。
获取树
如果你要通过左值和右值来显示这个树的话,你要首先标识出你要获取的那些节点。例如,如果你想获得“Fruit”子树,你要选择那些左值在2到11的节点。用SQL语句表达:
SELECT * FROM tree WHERE lft BETWEEN 2 AND 11;
这个会返回:

好吧,现在整个树都在一个查询中了。现在就要像前面的递归函数那样显示这个树,我们要加入一个ORDER BY子句在这个查询中。如果你从表中添加和删除行,你的表可能就顺序不对了,我们因此需要按照他们的左值来进行排序。
SELECT * FROM tree WHERE lft BETWEEN 2 AND 11 ORDER BY lft ASC;
就只剩下缩进的问题了。
要显示树状结构,子节点应该比他们的父节点稍微缩进一些。我们可以通过保存一个右值的一个栈。每次你从一个节点的子节点开始时,你把这个节点的右值 添加到栈中。你也知道子节点的右值都比父节点的右值小,这样通过比较当前节点和栈中的前一个节点的右值,你可以判断你是不是在显示这个父节点的子节点。当 你显示完这个节点,你就要把他的右值从栈中删除。要获得当前节点的层数,只要数一下栈中的元素。

如果运行这段代码,你可以获得和上一部分讨论的递归函数一样的结果。而这个函数可能会更快一点:他不采用递归而且只是用了两个查询
节点的路径
有了新的算法,我们还要另找一种新的方法来获得指定节点的路径。这样,我们就需要这个节点的祖先的一个列表。
由于新的表结构,这不需要花太多功夫。你可以看一下,例如,4-5的“Cherry”节点,你会发现祖先的左值都小于4,同时右值都大于5。这样,我们就可以使用下面这个查询:
SELECT title FROM tree WHERE lft 5 ORDER BY lft ASC;
注意,就像前面的查询一样,我们必须使用一个ORDER BY子句来对节点排序。这个查询将返回:
+-------+
| title |
+-------+
| Food |
| Fruit |
| Red |
+-------+
我们现在只要把各行连起来,就可以得到“Cherry”的路径了。
有多少个后续节点?How Many Descendants
如果你给我一个节点的左值和右值,我就可以告诉你他有多少个后续节点,只要利用一点点数学知识。
因为每个后续节点依次会对这个节点的右值增加2,所以后续节点的数量可以这样计算:
descendants = (right – left - 1) / 2
利用这个简单的公式,我可以立刻告诉你2-11的“Fruit”节点有4个后续节点,8-9的“Banana”节点只是1个子节点,而不是父节点。
自动化树遍历
现在你对这个表做一些事情,我们应该学习如何自动的建立表了。这是一个不错的练习,首先用一个小的树,我们也需要一个脚本来帮我们完成对节点的计数。
让我们先写一个脚本用来把一个邻接列表转换成前序遍历树表格。

这是一个递归函数。你要从rebuild_tree('Food',1); 开始,这个函数就会获取所有的“Food”节点的子节点。
如果没有子节点,他就直接设置它的左值和右值。左值已经给出了,1,右值则是左值加1。如果有子节点,函数重复并且返回最后一个右值。这个右值用来作为“Food”的右值。
递归让这个函数有点复杂难于理解。然而,这个函数确实得到了同样的结果。他沿着树走,添加每一个他看见的节点。你运行了这个函数之后,你会发现左值和右值和预期的是一样的(一个快速检验的方法:根节点的右值应该是节点数量的两倍)。
添加一个节点
我们如何给这棵树添加一个节点?有两种方式:在表中保留“parent”列并且重新运行rebuild_tree() 函数——一个很简单但却不是很优雅的函数;或者你可以更新所有新节点右边的节点的左值和右值。
第一个想法比较简单。你使用邻接列表方法来更新,同时使用改进前序遍历树来查询。如果你想添加一个新的节点,你只需要把节点插入表格,并且设置好parent列。然后,你只需要重新运行rebuild_tree() 函数。这做起来很简单,但是对大的树效率不高。
第二种添加和删除节点的方法是更新新节点右边的所有节点。让我们看一下例子。我们要添加一种新的水果——“Strawberry”,作为“Red” 的最后一个子节点。首先,我们要腾出一个空间。“Red”的右值要从6变成8,7-10的“Yellow”节点要变成9-12,如此类推。更新“Red” 节点意味着我们要把所有左值和右值大于5的节点加上2。
我们用一下查询:
UPDATE tree SET rgt=rgt+2 WHERE rgt>5;
UPDATE tree SET lft=lft+2 WHERE lft>5;
现在我们可以添加一个新的节点“Strawberry”来填补这个新的空间。这个节点左值为6右值为7。
INSERT INTO tree SET lft=6, rgt=7, title='Strawberry';
如果我们运行display_tree() 函数,我们将发现我们新的“Strawberry”节点已经成功地插入了树中:Food
Fruit
Red
Cherry
Strawberry
Yellow
Banana
Meat
Beef
Pork
缺点
首先,改进前序遍历树算法看上去很难理解。它当然没有邻接列表方法简单。然而,一旦你习惯了左值和右值这两个属性,他就会变得清晰起来,你可以用这个技术来完成临街列表能完成的所有事情,同时改进前序遍历树算法更快。当然,更新树需要很多查询,要慢一点,但是取得节点却可以只用一个查询。
你现在已经对两种在数据库存储树方式熟悉了吧。虽然在我这儿改进前序遍历树算法性能更好,但是也许在你特殊的情况下邻接列表方法可能表现更好一些。这个就留给你自己决定了
最后一点:就像我已经说得我部推荐你使用节点的标题来引用这个节点。你应该遵循数据库标准化的基本规则。我没有使用数字标识是因为用了之后例子就比较难读。
算法3
(
id INTEGER NOT NULL AUTO_INCREMENT,
parent_id INTEGER,
node VARCHAR(255),
PRIMARY KEY (id)
)
Articles Liés
Voir plus- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Comment utiliser cURL pour implémenter les requêtes Get et Post en PHP
- Tous les symboles d'expression dans les expressions régulières (résumé)

