Comprendre l'algorithme de tri rapide (avec des exemples en Java)

Explication détaillée de l'algorithme QuickSort : un outil de tri efficace

QuickSort est un algorithme de tri efficace basé sur la stratégie diviser pour régner. La méthode diviser pour régner décompose le problème en sous-problèmes plus petits, résout ces sous-problèmes séparément, puis combine les solutions des sous-problèmes pour obtenir la solution finale. Dans le tri rapide, un tableau est divisé en sélectionnant un élément de partition, qui détermine le point de division du tableau. Avant le partitionnement, la position de l'élément de partitionnement est réorganisée de manière à ce qu'il soit avant l'élément qui est plus grand que lui et après l'élément qui est plus petit que lui. Les sous-tableaux gauche et droit seront divisés de manière récursive de cette manière jusqu'à ce que chaque sous-tableau ne contienne qu'un seul élément, auquel cas le tableau est trié.

Fonctionnement du tri rapide

Trions le tableau suivant par ordre croissant à titre d'exemple :

Étape 1 : Sélectionnez l'élément pivot

On choisit le dernier élément comme pivot :

Étape 2 : Réorganiser les éléments de pivot

Nous plaçons l'élément pivot avant les éléments qui sont plus grands que lui et après les éléments qui sont plus petits que lui. Pour ce faire, nous allons parcourir le tableau et comparer le pivot à chaque élément qui le précède. Si un élément plus grand que le pivot est trouvé, nous créons un deuxième pointeur pour celui-ci :

Si un élément plus petit que le pivot est trouvé, on l'échange avec le deuxième pointeur :

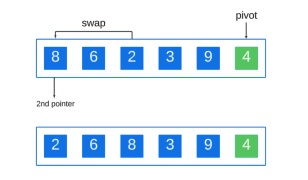
Répétez ce processus, en définissant l'élément suivant plus grand que le pivot sur le deuxième pointeur, en échangeant si un élément plus petit que le pivot est trouvé :

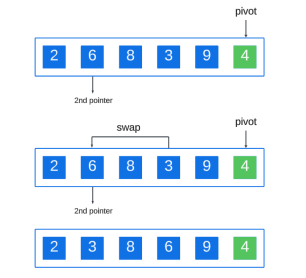
Continuez ce processus jusqu'à atteindre la fin du tableau :

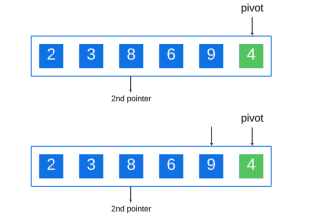
Après avoir terminé la comparaison des éléments, l'élément plus petit que le pivot a été déplacé vers la droite, puis on échange le pivot avec le deuxième pointeur :

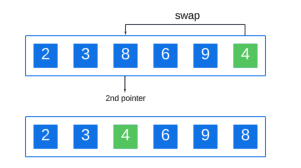
Étape 3 : Divisez le tableau

Divisez le tableau en fonction de l'index de partition. Si nous représentons le tableau comme arr[start..end], alors en divisant le tableau par partition, nous pouvons obtenir le sous-tableau gauche arr[start..partitionIndex-1] et le sous-tableau droit arr[partitionIndex 1..end].

Continuez à diviser les sous-tableaux de cette manière jusqu'à ce que chaque sous-tableau ne contienne qu'un seul élément :

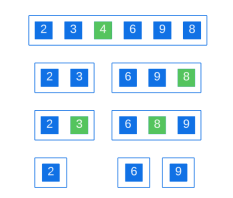
À ce stade, le tableau est trié.

Implémentation du code de tri rapide

<code class="language-java">import java.util.Arrays;

public class QuickSortTest {
    public static void main(String[] args){
        int[] arr = {8, 6, 2, 3, 9, 4};
        System.out.println("未排序数组: " + Arrays.toString(arr));
        quickSort(arr, 0, arr.length-1);
        System.out.println("已排序数组: " + Arrays.toString(arr));
    }

    public static int partition(int[] arr, int start, int end){
        // 将最后一个元素设置为枢轴
        int pivot = arr[end];
        // 创建指向下一个较大元素的指针
        int secondPointer = start-1;

        // 将小于枢轴的元素移动到枢轴左侧
        for (int i = start; i < end; i++){
            if (arr[i] < pivot){
                secondPointer++;
                // 交换元素
                int temp = arr[secondPointer];
                arr[secondPointer] = arr[i];
                arr[i] = temp;
            }
        }
        // 将枢轴与第二个指针交换
        int temp = arr[secondPointer+1];
        arr[secondPointer+1] = arr[end];
        arr[end] = temp;
        // 返回分区索引
        return secondPointer+1;
    }

    public static void quickSort(int[] arr, int start, int end){
        if (start < end){
            // 找到分区索引
            int partitionIndex = partition(arr, start, end);
            // 递归调用快速排序
            quickSort(arr, start, partitionIndex-1);
            quickSort(arr, partitionIndex+1, end);
        }
    }
}</code>

Interprétation du code

Méthode

quickSort : appelez d'abord la méthode partition pour diviser le tableau en deux sous-tableaux, puis appelez quickSort de manière récursive pour trier les sous-tableaux gauche et droit. Ce processus se poursuit jusqu'à ce que tous les sous-tableaux contiennent exactement un élément, auquel cas le tableau est trié.

partition Méthode : responsable de la division du tableau en deux sous-tableaux. Il définit d'abord le pivot et le pointeur sur l'élément le plus grand suivant, puis parcourt le tableau, déplaçant les éléments plus petits que le pivot vers la gauche. Après cela, il échange le pivot avec le deuxième pointeur et renvoie la position de la partition.

Exécutez le code ci-dessus, la console affichera ce qui suit :

Tableau non trié : [8, 6, 2, 3, 9, 4] Tableau trié : [2, 3, 4, 6, 8, 9]

Complexité temporelle

Meilleur des cas (O(n log n)) : Le meilleur des cas se produit lorsque le pivot divise le tableau en deux parties presque égales à chaque fois.

Cas moyen (O(n log n)) : Dans le cas moyen, le pivot divise le tableau en deux parties inégales, mais la profondeur de récursion et le nombre de comparaisons sont toujours proportionnels à n log n.

Pire des cas (O(n²)) : Le pire des cas se produit lorsque le pivot divise toujours le tableau en parties très inégales (par exemple, une partie n'a qu'un seul élément et l'autre a n-1 éléments). Cela peut se produire, par exemple, lors du tri d'un tableau dans l'ordre inverse et que le pivot est mal choisi.

Complexité spatiale (O(log n)) : le tri rapide est généralement implémenté sur place et ne nécessite pas de tableaux supplémentaires.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!