Inverser les niveaux impairs de l'arbre binaire

2415. Inverser les niveaux impairs de l'arbre binaire

Difficulté :Moyen

Sujets : Arbre, recherche en profondeur d'abord, recherche en largeur d'abord, arbre binaire

Étant donné la racine d'un arbre binaire parfait, inversez les valeurs des nœuds à chaque niveau impair de l'arbre.

• Par exemple, supposons que les valeurs du nœud au niveau 3 soient [2,1,3,4,7,11,29,18], alors elles devraient devenir [18,29,11,7,4,3,1 ,2].

Renvoyer la racine de l'arbre inversé.

Un arbre binaire est parfait si tous les nœuds parents ont deux enfants et que toutes les feuilles sont au même niveau.

Le niveau d'un nœud est le nombre d'arêtes le long du chemin entre celui-ci et le nœud racine.

Exemple 1 :

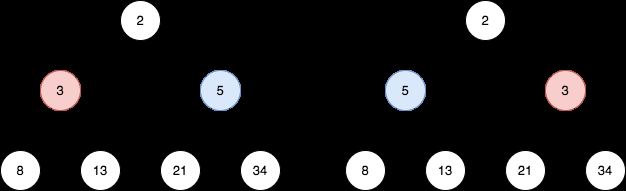
• Entrée : racine = [2,3,5,8,13,21,34]
• Sortie : [2,5,3,8,13,21,34]
• Explication :
  • L'arbre n'a qu'un seul niveau impair.
  • Les nœuds au niveau 1 sont respectivement 3, 5, qui s'inversent et deviennent 5, 3.

Exemple 2 :

• Entrée : racine = [7,13,11]
• Sortie : [7,11,13]
• Explication :
  • Les nœuds au niveau 1 sont 13, 11, qui s'inversent et deviennent 11, 13.

Exemple 3 :

• Entrée : racine = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
• Sortie : [0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
• Explication :
  • Les niveaux impairs ont des valeurs non nulles.
  • Les nœuds au niveau 1 étaient 1, 2, et sont 2, 1 après l'inversion.
  • Les nœuds au niveau 3 étaient 1, 1, 1, 1, 2, 2, 2, 2, et sont 2, 2, 2, 2, 1, 1, 1, 1 après l'inversion.

Contraintes :

• Le nombre de nœuds dans l'arborescence est compris entre [1, 2¹⁴].
• 0 <= Node.val <= 10⁵
• la racine est un arbre binaire parfait.

Indice :

1. Essayez de résoudre de manière récursive pour chaque niveau indépendamment.
2. Lorsque vous effectuez une recherche en profondeur d'abord, passez les nœuds gauche et droit (qui doivent être appariés) au niveau suivant. Si le niveau actuel est impair, inversez leurs valeurs, ou bien passez de manière récursive au niveau suivant.

Solution :

Nous devons effectuer une traversée en profondeur d'abord sur l'arbre binaire. La tâche consiste à inverser les valeurs des nœuds à des niveaux impairs. Un arbre binaire parfait signifie que tous les nœuds non-feuilles ont deux enfants et que tous les nœuds feuilles sont au même niveau.

Nous utiliserons une approche DFS (Depth-First Search), et à chaque niveau impair, nous inverserons les valeurs des nœuds. Vous trouverez ci-dessous la solution qui permet d'y parvenir.

Points clés :

• L'arbre est parfait, c'est-à-dire qu'il est complètement équilibré et que tous les nœuds des feuilles sont au même niveau.
• Seuls les nœuds aux niveaux impairs doivent être inversés. Les niveaux impairs sont indexés à partir du niveau 1 (1er, 3ème, 5ème, etc.).
• Un DFS peut être utilisé pour parcourir l'arborescence et identifier les niveaux de nœuds. Lorsque nous rencontrons un niveau impair, nous échangeons les valeurs des nœuds à ce niveau.
• A chaque niveau, nous parcourons deux nœuds enfants : l'enfant gauche et l'enfant droit.

Approche:

1. Effectuez une traversée de l'arbre en profondeur d'abord.
2. Pour chaque paire de nœuds au niveau actuel :
   • Si le niveau est impair, échangez les valeurs des nœuds.
3. Traitez de manière récursive les enfants gauche et droit du nœud actuel, en transmettant les informations de niveau mises à jour.
4. Renvoyer le nœud racine après avoir traité l'intégralité de l'arborescence.

Plan:

1. Commencez à partir du nœud racine.
2. Utilisez une fonction récursive dfs pour parcourir l'arbre et inverser les valeurs des nœuds à des niveaux impairs.
3. Gardez une trace du niveau actuel pour identifier les niveaux impairs.
4. Échangez les valeurs à des niveaux impairs et continuez le parcours DFS pour les enfants.
5. Renvoyer la racine après le traitement.

Étapes de la solution :

1. Définir une fonction récursive dfs($left, $right, $isOddLevel) :
   • gauche : nœud enfant gauche.
   • à droite : nœud enfant droit.
   • isOddLevel : booléen indiquant si le niveau actuel est impair.
2. Vérifiez si left est nul. Si c'est le cas, revenez, car il n'y a plus de nœuds à traiter.
3. Si isOddLevel est vrai, échangez les valeurs des nœuds gauche et droit.
4. Appelez récursivement la fonction dfs pour :
   • Enfant gauche de gauche et enfant droit de droite (niveau suivant).
   • Enfant droit de gauche et enfant gauche de droite (niveau suivant).
5. Démarrez la récursivité avec dfs($root->left, $root->right, true) et renvoyez la racine.

Implémentons cette solution en PHP : 2415. Inverser les niveaux impairs de l'arbre binaire


<?php
class TreeNode {
    public $val = 0;
    public $left = null;
    public $right = null;

    public function __construct($val = 0, $left = null, $right = null) {
        $this->val = $val;
        $this->left = $left;
        $this->right = $right;
    }
}

class Solution {
    /**
     * @param TreeNode $root
     * @return TreeNode
     */
    public function reverseOddLevels($root) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * Helper function to perform DFS
     *
     * @param $left
     * @param $right
     * @param $isOddLevel
     * @return void
     */
    private function dfs($left, $right, $isOddLevel) {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

// Example usage:
$root = new TreeNode(2);
$root->left = new TreeNode(3);
$root->right = new TreeNode(5);
$root->left->left = new TreeNode(8);
$root->left->right = new TreeNode(13);
$root->right->left = new TreeNode(21);
$root->right->right = new TreeNode(34);

$solution = new Solution();
$reversedRoot = $solution->reverseOddLevels($root);

// Function to print the tree for testing
function printTree($root) {
    if ($root === null) {
        return;
    }
    echo $root->val . " ";
    printTree($root->left);
    printTree($root->right);
}

printTree($reversedRoot); // Output: 2 5 3 8 13 21 34
?>

Explication:

1. Classe TreeNode : Représente la structure d'un nœud d'arbre binaire, qui a une valeur (val) et deux enfants (gauche, droite).
2. Fonction reverseOddLevels : lance le DFS avec les enfants gauche et droit du nœud racine et démarre au niveau 1 (niveau impair).
3. Fonction dfs :
   • Prend deux nœuds (gauche et droite) et un booléen isOddLevel pour déterminer si le niveau actuel est impair.
   • Si le niveau actuel est impair, les valeurs de gauche et de droite sont inversées.
   • S'appelle récursivement pour le niveau suivant, en alternant la valeur isOddLevel (vrai devient faux et vice versa).
4. La récursion procède au traitement de la paire de nœuds suivante à chaque niveau, garantissant que seuls les nœuds aux niveaux impairs sont inversés.

Exemple de procédure pas à pas :

Exemple 1 :

Entrée :


       2
      / \
     3   5
    / \ / \
   8 13 21 34

• Niveau 0 : [2] (pair, pas de changement).
• Niveau 1 : [3, 5] (impair, inverse à [5, 3]).
• Niveau 2 : [8, 13, 21, 34] (pair, pas de changement).

Sortie :


       2
      / \
     5   3
    / \ / \
   8 13 21 34

Exemple 2 :

Entrée :


       7
      / \
     13  11

• Niveau 0 : [7] (pair, pas de changement).
• Niveau 1 : [13, 11] (impair, inverse à [11, 13]).

Sortie :


       7
      / \
     11  13

Complexité temporelle :

• Complexité temporelle : O(n), où n est le nombre de nœuds dans l'arbre binaire. Nous visitons chaque nœud exactement une fois, en profondeur.
• Complexité spatiale : O(h), où h est la hauteur de l'arbre. La profondeur de récursion correspond à la hauteur de l'arbre, et dans le pire des cas (pour un arbre asymétrique), ce serait O(n), mais pour un arbre binaire parfait, c'est O(log n).

Cette solution inverse efficacement les nœuds aux niveaux impairs d'un arbre binaire parfait en utilisant une recherche en profondeur d'abord avec une complexité temporelle de O(n). Le code échange les valeurs à des niveaux impairs et utilise une approche récursive pour traiter l'arborescence.

Liens de contact

Si vous avez trouvé cette série utile, pensez à donner une étoile au référentiel sur GitHub ou à partager la publication sur vos réseaux sociaux préférés ?. Votre soutien signifierait beaucoup pour moi !

Si vous souhaitez du contenu plus utile comme celui-ci, n'hésitez pas à me suivre :

• LinkedIn
• GitHub

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!