Descente de gradient par lots, mini-lots et stochastiques

Achetez-moi un café☕

*Mémos :

• Mon article explique Batch, Mini-Batch et Stochastic Gradient Descent avec DataLoader() dans PyTorch.
• Mon article explique la descente de gradient par lots sans DataLoader() dans PyTorch.
• Mon article explique les optimiseurs dans PyTorch.

Il existe des descentes de gradient par lots (BGD), des descentes de gradient par mini-lots (MBGD) et des descentes de gradient stochastiques (SGD) qui sont des moyens de comment extraire des données d'un ensemble de données pour effectuer une descente de gradient avec le optimiseurs tels que Adam(), SGD(), RMSprop(), Adadelta(), Adagrad(), etc. dans PyTorch.

*Mémos :

• SGD() dans PyTorch n'est que la descente de gradient de base sans fonctionnalités spéciales (Decente de gradient classique (CGD)) mais pas de descente de gradient stochastique (SGD).
• Par exemple, en utilisant les méthodes ci-dessous, vous pouvez faire de manière flexible BGD, MBGD ou SGD Adam avec Adam(), CGD avec SGD(), RMSprop avec RMSprop(), Adadelta avec Adadelta(), Adagrad avec Adagrad(), etc dans PyTorch.
• Fondamentalement, BGD, MBGD ou SGD est réalisé avec un ensemble de données mélangées avec DataLoader() : *Mémos :
  • Le brassage des ensembles de données atténue le surapprentissage. *Fondamentalement, seules les données du train sont mélangées, donc les données de test ne sont pas mélangées.
  • Mon article explique le surajustement et le sous-ajustement.

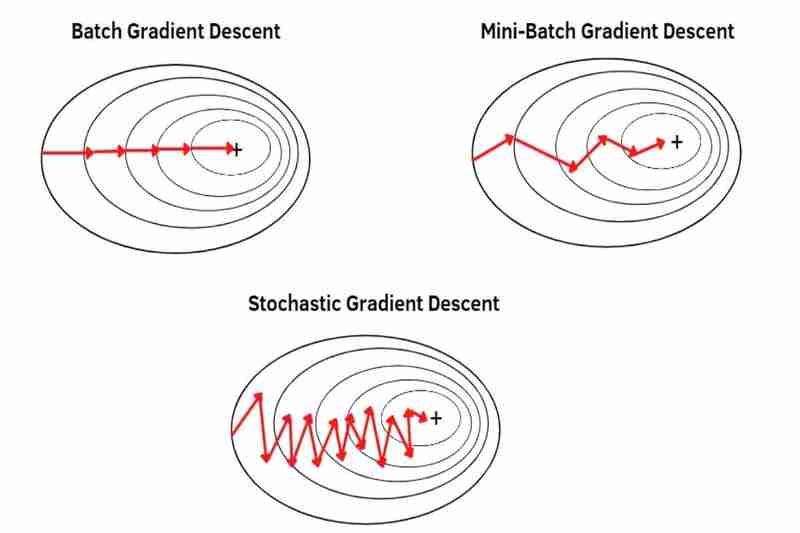
(1) Descente de gradient par lots (BGD) :

• peut effectuer une descente de gradient avec un ensemble de données complet, en ne faisant qu'un seul pas par époque. Par exemple, un ensemble de données complet contient 100 échantillons (1x100), puis la descente de gradient ne se produit qu'une seule fois par époque, ce qui signifie que les paramètres du modèle ne sont mis à jour qu'une seule fois par époque.
• utilise la moyenne de tout un ensemble de données, de sorte que chaque échantillon est moins mis en évidence (moins souligné) que MBGD et SGD. En conséquence, la convergence est plus stable (moins fluctuée) que MBGD et SGD et également plus forte en bruit (données bruyantes) que MBGD et SGD, provoquant moins de dépassements que MBGD et SGD et créant un modèle plus précis que MBGD et SGD si pas resté coincé dans les minima locaux mais BGD échappe moins facilement aux minima locaux ou aux points de selle que MBGD et SGD car la convergence est plus stable(moins fluctuée) que MBGD et SGD comme je l'ai déjà dit et BGD provoquent plus facilement un surapprentissage que MBGD et SGD car chaque échantillon est moins mis en évidence (moins souligné) que MBGD et SGD comme je l'ai déjà dit. *Mémos :
  • Convergence signifie qu'un poids initial se déplace vers le minimum global d'une fonction par descente de gradient.
  • Bruit(données bruyantes) signifie des valeurs aberrantes, des anomalies ou des données parfois dupliquées.
  • Dépasser signifie sauter par-dessus le minimum global d'une fonction.
Les avantages de
•  :
  • La convergence est plus stable (moins fluctuée) que MBGD et SGD.
  • Il est plus fort en bruit (données bruyantes) que MBGD et SGD.
  • Cela provoque moins de dépassement que MBGD et SGD.
  • Il crée un modèle plus précis que MBGD et SGD s'il n'est pas coincé dans les minima locaux.
Les inconvénients de
•  :
  • Ce n'est pas bon pour un grand ensemble de données tel que l'apprentissage en ligne, car cela prend beaucoup de mémoire, ce qui ralentit la convergence. *L'apprentissage en ligne est la manière dont un modèle apprend progressivement à partir d'un flux de données en temps réel.
  • Il nécessite la préparation d'un ensemble de données complet si vous souhaitez mettre à jour un modèle.
  • Il échappe moins facilement aux minima locaux ou aux points de selle que MBGD et SGD.
  • Cela provoque plus facilement un surapprentissage que MBGD et SGD.

(2) Descente de gradient en mini-lots (MBGD) :

• peut effectuer une descente de gradient avec un ensemble de données divisé (les petits lots d'un ensemble de données entier), un petit lot par un petit lot, en prenant le même nombre d'étapes que les petits lots d'un ensemble de données entier en une seule époque. Par exemple, l'ensemble de données contenant 100 échantillons (1x100) est divisé en 5 petits lots (5x20), puis la descente de gradient se produit 5 fois au cours d'une époque, ce qui signifie que les paramètres du modèle sont mis à jour 5 fois au cours d'une époque.

• utilise la moyenne de chaque petit lot divisée à partir d'un ensemble de données complet afin que chaque échantillon se démarque davantage (plus mis en valeur) que BDG. * Diviser un ensemble de données entier en lots plus petits peut faire en sorte que chaque échantillon se démarque de plus en plus (de plus en plus souligné). En conséquence, la convergence est moins stable (plus fluctuée) que BGD et également moins forte en bruit (données bruyantes) que BGD, provoquant davantage de dépassements que BGD et créant un modèle moins précis que BGD même s'il n'est pas resté coincé dans les minima locaux mais MBGD échappe plus facilement aux minima locaux ou aux points de selle que BGD car la convergence est moins stable (plus fluctuée) que BGD comme je l'ai dit précédemment et MBGD provoque moins facilement surapprentissage que BGD car chaque échantillon est plus mis en évidence (plus souligné) que BGD comme je l'ai déjà dit.

• Les avantages de

   :

  • C'est mieux pour un grand ensemble de données tel que l'apprentissage en ligne que BGD car il nécessite moins de mémoire que BGD, ce qui ralentit moins la convergence que BGD.
  • Il n'est pas nécessaire de repréparer un ensemble de données complet si vous souhaitez mettre à jour un modèle.
  • Il échappe plus facilement aux minima locaux ou aux points de selle que le BGD.
  • Il provoque moins facilement un surapprentissage que le BGD.
• Les inconvénients de

   :

  • La convergence est moins stable (plus fluctuée) que BGD.
  • Il est moins fort en bruit (données bruyantes) que BGD.
  • Cela provoque davantage un dépassement que le BGD.
  • Cela crée un modèle moins précis que BGD même s'il n'est pas coincé dans les minima locaux.

(3) Descente de gradient stochastique (SGD) :

• peut effectuer une descente de gradient avec chaque échantillon d'un ensemble de données entier, un échantillon par un échantillon, en prenant le même nombre d'étapes que les échantillons d'un ensemble de données entier à une époque. Par exemple, un ensemble de données complet contient 100 échantillons (1x100), puis la descente de gradient se produit 100 fois au cours d'une époque, ce qui signifie que les paramètres du modèle sont mis à jour 100 fois au cours d'une époque.

• utilise chaque échantillon d'un ensemble de données entier un échantillon par échantillon mais pas la moyenne, donc chaque échantillon se démarque davantage (plus souligné) que MBGD. En conséquence, la convergence est moins stable (plus fluctuée) que MBGD et également moins forte en bruit (données bruyantes) que MBGD, provoquant davantage de dépassements que MBGD et créant un modèle moins précis que MBGD même s'il n'est pas resté coincé dans les minima locaux mais SGD échappe plus facilement aux minima locaux ou aux points selles que MBGD car la convergence est moins stable (plus fluctuée) que MBGD comme je l'ai déjà dit et SGD provoque moins facilement un surajustement que MBGD car chaque échantillon est plus mis en valeur que MBGD comme je l'ai déjà dit.

• Les avantages de

   :

  • Il est meilleur que MBGD pour un ensemble de données volumineux tel que l'apprentissage en ligne, car il nécessite moins de mémoire que MBGD, ce qui ralentit moins la convergence que MBGD.
  • Il n'est pas nécessaire de repréparer un ensemble de données complet si vous souhaitez mettre à jour un modèle.
  • Il échappe plus facilement aux minima locaux ou aux points de selle que MBGD.
  • Il provoque moins facilement un surapprentissage que MBGD.
• Les inconvénients de

   :

  • La convergence est moins stable (plus fluctuée) que MBGD.
  • Il est moins fort en bruit (données bruyantes) que MBGD.
  • Cela provoque davantage de dépassement que MBGD.
  • Cela crée un modèle moins précis que MBGD s'il n'est pas coincé dans les minimums locaux.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!