Maison >développement back-end >Tutoriel Python >Notation Big O - Python
Notation Big O - Python
- Barbara Streisandoriginal
- 2024-11-18 08:43:01846parcourir
1. Définition
Notation mathématique qui décrit la limite supérieure du temps d'exécution ou de l'utilisation de l'espace d'un algorithme. Il est noté O(f(n)), où f(n) est une fonction qui représente le temps ou l'espace en fonction de la taille de l'entrée n .
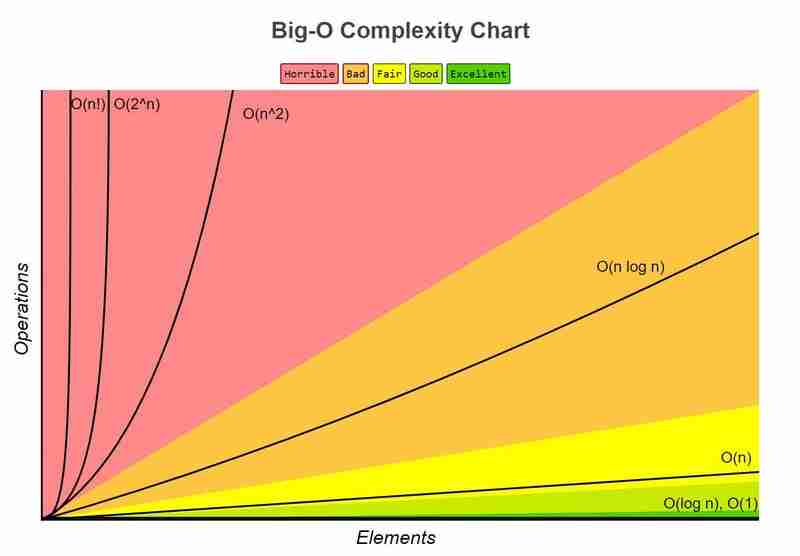
Pour plus d'informations, visitez : http://bigoheatsheet.com
2. Objectif
- Comparaison d'algorithmes : Permet de comparer différents algorithmes et de choisir le plus efficace pour un problème donné.
- Évolutivité : aide à prédire le comportement d'un algorithme lorsque la quantité de données augmente.
3. Analyse de complexité
- Pire des cas : fait référence au scénario dans lequel l'algorithme prend plus de temps ou utilise plus de ressources. Big O fait généralement référence à ce cas.
- Meilleur cas et cas moyen : bien qu'importants, ils sont utilisés moins fréquemment pour la notation Big O.
4. Espace contre Temps
- Complexité temporelle : fait référence au temps nécessaire à l'exécution d'un algorithme.
- Complexité spatiale : fait référence à la quantité de mémoire supplémentaire qu'il utilise. Il peut avoir des notations comme O(1) (espace constant) ou O(n) (espace linéaire).
Exemple :
import timeit
import matplotlib.pyplot as plt
import cProfile
# O(1)
def constant_time_operation():
return 42
# O(log n)
def logarithmic_time_operation(n):
count = 0
while n > 1:
n //= 2
count += 1
return count
# O(n)
def linear_time_operation(n):
total = 0
for i in range(n):
total += i
return total
# O(n log n)
def linear_logarithmic_time_operation(n):
if n <= 1:
return n
else:
return linear_logarithmic_time_operation(n - 1) + n
# O(n^2)
def quadratic_time_operation(n):
total = 0
for i in range(n):
for j in range(n):
total += i + j
return total
# O(2^n)
def exponential_time_operation(n):
if n <= 1:
return 1
else:
return exponential_time_operation(n - 1) + exponential_time_operation(n - 1)
# O(n!)
def factorial_time_operation(n):
if n == 0:
return 1
else:
return n * factorial_time_operation(n - 1)
# Function to measure execution time using timeit
def measure_time(func, *args):
execution_time = timeit.timeit(lambda: func(*args), number=1000)
return execution_time
def plot_results(results):
functions, times = zip(*results)
colors = ['skyblue', 'orange', 'green', 'red', 'purple', 'brown', 'pink']
plt.figure(figsize=(14, 8))
plt.bar(functions, times, color=colors)
for i, v in enumerate(times):
plt.text(i, v + 0.5, f"{v:.6f}", ha='center',
va='bottom', rotation=0, color='black')
plt.xlabel('Function Complexity')
plt.ylabel('Average Time (s)')
plt.title('Execution Time of Different Algorithm Complexities')
plt.grid(axis='y', linestyle='--', linewidth=0.5, color='gray', alpha=0.5)
plt.tight_layout()
plt.show()
def main():
results = []
results.append(("O(1)", measure_time(constant_time_operation)))
results.append(("O(log n)", measure_time(logarithmic_time_operation, 10)))
results.append(("O(n)", measure_time(linear_time_operation, 10)))
results.append(("O(n log n)", measure_time(
linear_logarithmic_time_operation, 10)))
results.append(("O(n^2)", measure_time(quadratic_time_operation, 7)))
results.append(("O(2^n)", measure_time(exponential_time_operation, 7)))
results.append(("O(n!)", measure_time(factorial_time_operation, 112)))
plot_results(results)
if __name__ == '__main__':
cProfile.run("main()", sort="totime", filename="output_profile.prof")
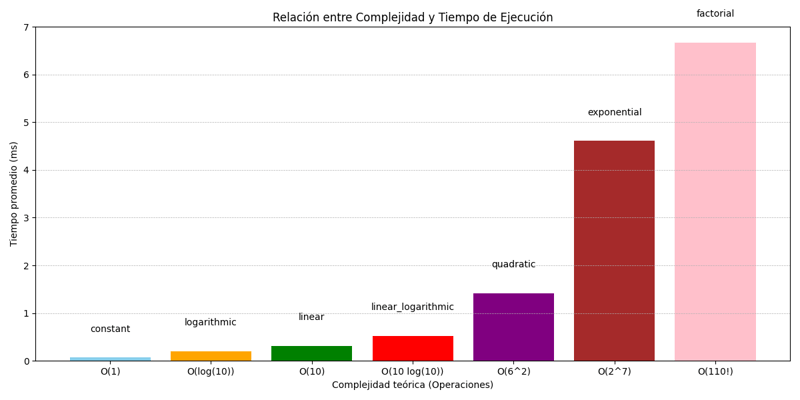
N'oubliez pas qu'il ne suffit pas d'appliquer simplement une grande notation ou, bien que ce soit la première étape, il existe d'autres moyens d'optimiser la mémoire, par exemple l'utilisation de emplacements, de cache, de threads, de parallélisme, processus, etc.
Merci d'avoir lu !!
Soutenez-moi en réagissant et en donnant votre avis.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

