Comprendre l'algorithme de tri par fusion : guide du débutant pour maîtriser l'algorithme de tri

Dans nos articles précédents, nous avons découvert un certain nombre d'algorithmes de tri tels que le tri à bulles, le tri par sélection ainsi que le tri par insertion. Nous avons appris que même si ces algorithmes de tri sont très faciles à mettre en œuvre, ils ne sont pas efficaces pour les grands ensembles de données, ce qui signifie que nous avons besoin d'un algorithme plus efficace pour gérer le tri des grands ensembles de données, et donc le tri par fusion. Dans cette série, nous verrons comment fonctionne le tri par fusion et comment il peut être implémenté en JavaScript. Tu es prêt ?

Table des matières

1. Qu'est-ce que l'algorithme de tri par fusion ?
2. Comment fonctionnent les algorithmes de tri par fusion
   • Complexité temporelle
   • Complexité spatiale
3. Implémentation en JavaScript
4. Conclusion

Qu’est-ce que l’algorithme de tri par fusion ?

Merge Sort Algorithm est un excellent algorithme de tri qui suit le principe diviser pour régner. Contrairement aux algorithmes plus simples comme le tri par sélection et le tri à bulles qui effectuent plusieurs passages dans le tableau en comparant les éléments adjacents, le tri par fusion adopte une approche plus stratégique :

1. Diviser : tout d'abord, le tri par fusion divise le tableau en deux moitiés
2. Conquérir : deuxièmement, il trie récursivement chaque moitié
3. Combiner : enfin, il fusionne les moitiés triées ensemble

Cette approche surpasse systématiquement les algorithmes O(n²) plus simples tels que le tri par sélection et le tri à bulles lorsqu'il s'agit de jeux de données plus volumineux.

Comment fonctionnent les algorithmes de tri par fusion

Nous avons vu que le tri par fusion fonctionne en utilisant l'approche populaire diviser pour régner. Vous trouverez ci-dessous une représentation visuelle de son fonctionnement.

Maintenant que nous avons vu la magie, voyons comment fonctionne l'algorithme de tri par fusion en triant manuellement ce tableau : [38, 27, 43, 3, 9, 82, 10] en utilisant l'approche mentionnée ci-dessus.

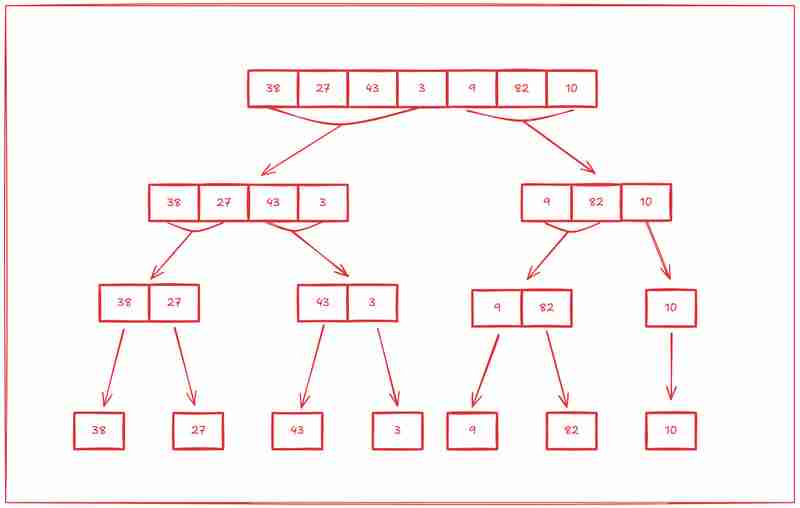
Étape 1 : Diviser

La première étape du tri par fusion consiste à diviser le tableau en sous-tableaux, puis à diviser chaque sous-tableau en sous-tableaux, et le sous-tableau en sous-tableaux jusqu'à ce qu'il ne reste qu'un seul élément dans tous les sous-tableaux.

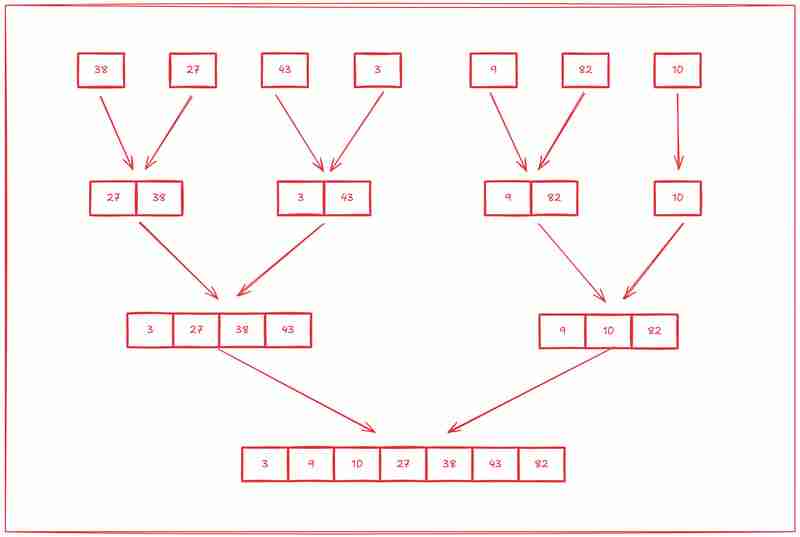
Étape 2 : Fusionner (Conquérir)

La deuxième étape consiste à commencer à trier ces sous-réseaux à partir de zéro.

Complexité temporelle

Le tri par fusion atteint une complexité temporelle O(n log n) dans tous les cas (meilleur, moyen et pire), ce qui le rend plus efficace que les algorithmes O(n²) pour les ensembles de données plus volumineux.

Voici pourquoi :

• Division : Le tableau est divisé log n fois (chaque division réduit la taille de moitié)
• Fusion : Chaque niveau de fusion nécessite n opérations
• Total : n opérations × log n niveaux = O(n log n)

Comparez ceci à :

• Tri à bulles : O(n²)
• Tri de sélection : O(n²)
• Tri par fusion : O(n log n)

Pour un tableau de 1 000 éléments :

• O(n²) ≈ 1 000 000 d'opérations
• O(n log n) ≈ 10 000 opérations

Complexité spatiale

Le tri par fusion nécessite O(n) espace supplémentaire pour stocker les tableaux temporaires pendant la fusion. Bien que ce soit plus que l'espace O(1) nécessaire au tri à bulles ou au tri par sélection, l'efficacité du temps rend généralement ce compromis intéressant dans la pratique.

Implémentation en JavaScript

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

Décomposer la fonction de fusion :

1. Configuration des fonctions :

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

• Crée un tableau vide pour stocker les résultats fusionnés
• Initialise les pointeurs pour les deux tableaux d'entrée
• Pensez à ces pointeurs comme des doigts qui indiquent où nous nous trouvons dans chaque tableau

1. Logique de fusion principale :

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

• Compare les éléments des deux tableaux
• Prend le plus petit élément et l'ajoute au résultat
• Déplace le pointeur vers l'avant dans le tableau que nous avons extrait
• C'est comme choisir la plus petite de deux cartes lors du tri d'un jeu

1. Phase de nettoyage :

   while (leftIndex < left.length) {
     result.push(left[leftIndex]);
     leftIndex++;
   }

• Ajoute tous les éléments restants
• Nécessaire car un tableau peut être plus long que l'autre
• Comme rassembler les cartes restantes après avoir comparé

La fonction principale de tri par fusion

function mergeSort(arr) {
  // Base case
  if (arr.length <= 1) {
    return arr;
  }

  // Divide
  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // Conquer and Combine
  return merge(mergeSort(left), mergeSort(right));
}

Décomposer le tri par fusion :

1. Cas de base :

   if (arr.length <= 1) {
     return arr;
   }

• Gère les tableaux de longueur 0 ou 1
• Ceux-ci sont déjà triés par définition
• Agit comme notre point d'arrêt de récursion

1. Phase de division :

   const middle = Math.floor(arr.length / 2);
   const left = arr.slice(0, middle);
   const right = arr.slice(middle);

• Divise le tableau en deux moitiés
• slice() crée de nouveaux tableaux sans modifier l'original
• C'est comme couper un jeu de cartes en deux

1. Tri et fusion récursifs :

   return merge(mergeSort(left), mergeSort(right));

• Trie récursivement chaque moitié
• Combine les moitiés triées à l'aide de la fonction de fusion
• Comme trier de petites piles de cartes avant de les combiner

Exemple de procédure pas à pas

Voyons comment ça trie [38, 27, 43, 3] :

1. Premier partage :

// The Merge Helper Function
function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] <= right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // Add remaining elements
  while (leftIndex < left.length) {
    result.push(left[leftIndex]);
    leftIndex++;
  }

  while (rightIndex < right.length) {
    result.push(right[rightIndex]);
    rightIndex++;
  }

  return result;
}

1. Deuxième division :

   const result = [];
   let leftIndex = 0;
   let rightIndex = 0;

1. Fusionner en arrière :

   while (leftIndex < left.length && rightIndex < right.length) {
     if (left[leftIndex] <= right[rightIndex]) {
       result.push(left[leftIndex]);
       leftIndex++;
     } else {
       result.push(right[rightIndex]);
       rightIndex++;
     }
   }

Conclusion

Merge Sort se distingue comme un algorithme de tri très efficace qui fonctionne systématiquement bien sur de grands ensembles de données. Bien qu'il nécessite un espace supplémentaire par rapport aux algorithmes de tri plus simples, sa complexité temporelle O(n log n) en fait un choix incontournable pour de nombreuses applications du monde réel où les performances sont cruciales.

Points clés à retenir :

• Utilise la stratégie diviser pour régner
• O(n log n) complexité temporelle dans tous les cas
• Nécessite O(n) espace supplémentaire
• Algorithme de tri stable
• Excellent pour les grands ensembles de données

---

---

Restez à jour et connecté

Pour vous assurer de ne manquer aucune partie de cette série et pour me contacter pour plus de détails
discussions sur le Développement Logiciel (Web, Serveur, Mobile ou Scraping/Automatisation), les données
structures et algorithmes, et d'autres sujets technologiques passionnants, suivez-moi sur :

Emmanuel Ayinde Suivez

Ingénieur logiciel | Rédacteur technique | Développeur Backend, Web & Mobile ? | Passionné par la création de solutions logicielles efficaces et évolutives. #connectons-nous ?

• GitHub
• Linkedin
• X (Twitter)

Restez à l'écoute et bon codage ?‍??

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!