Métriques pour les algorithmes de régression

Métriques d'erreur pour les algorithmes de régression

Lorsque nous créons un algorithme de régression et que nous voulons connaître l'efficacité de ce modèle, nous utilisons des métriques d'erreur pour obtenir des valeurs qui représentent l'erreur de notre modèle d'apprentissage automatique. Les métriques de cet article sont importantes lorsque l'on souhaite mesurer l'erreur des modèles de prédiction pour des valeurs numériques (réelles, entières).

Dans cet article, nous couvrirons les principales mesures d'erreur pour les algorithmes de régression, en effectuant les calculs manuellement en Python et en mesurant l'erreur du modèle d'apprentissage automatique sur un ensemble de données de cotation en dollars.

Métriques abordées

• SE — Somme d'erreur
• ME — Erreur moyenne
• MAE — Erreur moyenne absolue
• MPE — Pourcentage d'erreur moyen
• MAPAE — Erreur de pourcentage absolu moyen

Les deux métriques sont un peu similaires, où nous avons des métriques pour la moyenne et le pourcentage d'erreur et des métriques pour le pourcentage d'erreur moyen et absolu, différenciées de manière à ce qu'un seul groupe obtienne la valeur réelle de la différence et l'autre obtienne la valeur absolue. de la différence. Il est important de se rappeler que dans les deux métriques, plus la valeur est faible, meilleures sont nos prévisions.

SE — Somme d'erreur

La métrique SE est la plus simple de toutes dans cet article, où sa formule est :

SE = εR — P

C'est donc la somme de la différence entre la valeur réelle (variable cible du modèle) et la valeur prédite. Cette métrique présente quelques points négatifs, comme le fait de ne pas traiter les valeurs comme absolues, ce qui entraînera par conséquent une fausse valeur.

ME - Moyenne d'erreur

La métrique ME est un "complément" de la SE, où l'on a en gros la différence que l'on obtiendra une moyenne de la SE étant donné le nombre d'éléments :

ME = ε(R-P)/N

Contrairement à SE, nous divisons simplement le résultat SE par le nombre d'éléments. Cette métrique, comme SE, dépend de l'échelle, c'est-à-dire que nous devons utiliser le même ensemble de données et pouvoir comparer avec différents modèles de prévision.

MAE — Erreur absolue moyenne

La métrique MAE est la ME mais en considérant uniquement les valeurs absolues (non négatives). Lorsque nous calculons la différence entre le réel et le prévu, nous pouvons obtenir des résultats négatifs et cette différence négative est appliquée aux mesures précédentes. Dans cette métrique, il faut transformer la différence en valeurs positives puis prendre la moyenne en fonction du nombre d'éléments.

MPE — Pourcentage d'erreur moyen

La métrique MPE est l'erreur moyenne en pourcentage de la somme de chaque différence. Ici, il faut prendre le pourcentage de la différence, l'ajouter puis le diviser par le nombre d'éléments pour obtenir la moyenne. Par conséquent, la différence entre la valeur réelle et la valeur prédite est faite, divisée par la valeur réelle, multipliée par 100, nous additionnons tout ce pourcentage et divisons par le nombre d'éléments. Cette métrique est indépendante de l'échelle (%).

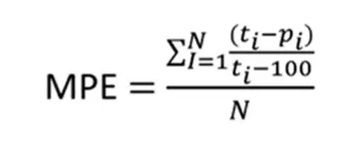
MAPAE — Erreur moyenne absolue en pourcentage

La métrique MAPAE est très similaire à la métrique précédente, mais la différence entre le prédit x réel est faite de manière absolue, c'est-à-dire que vous la calculez avec des valeurs positives. Par conséquent, cette mesure correspond à la différence absolue du pourcentage d’erreur. Cette métrique est également indépendante de l'échelle.

Utiliser les métriques en pratique

Étant donné une explication de chaque métrique, nous calculerons les deux manuellement en Python sur la base d'une prédiction à partir d'un modèle d'apprentissage automatique du taux de change du dollar. Actuellement, la plupart des métriques de régression existent dans des fonctions prêtes à l'emploi du package Sklearn, mais ici nous les calculerons manuellement à des fins pédagogiques uniquement.

Nous utiliserons les algorithmes RandomForest et Decision Tree uniquement pour comparer les résultats entre les deux modèles.

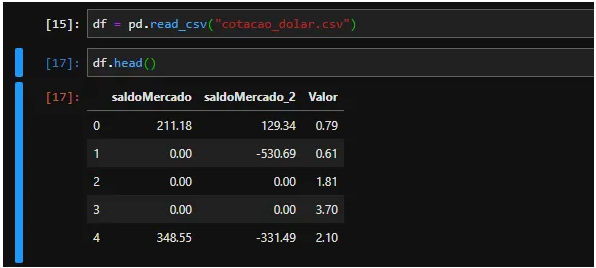
Analyse des données

Dans notre ensemble de données, nous avons une colonne SaldoMercado et saldoMercado_2 qui sont des informations qui influencent la colonne Valeur (notre cotation en dollars). Comme nous pouvons le constater, le solde MercadoMercado a une relation plus étroite avec la cotation que le solde Merado_2. Il est également possible d'observer qu'il ne nous manque pas de valeurs (valeurs infinies ou Nan) et que la colonne balanceMercado_2 possède de nombreuses valeurs non absolues.

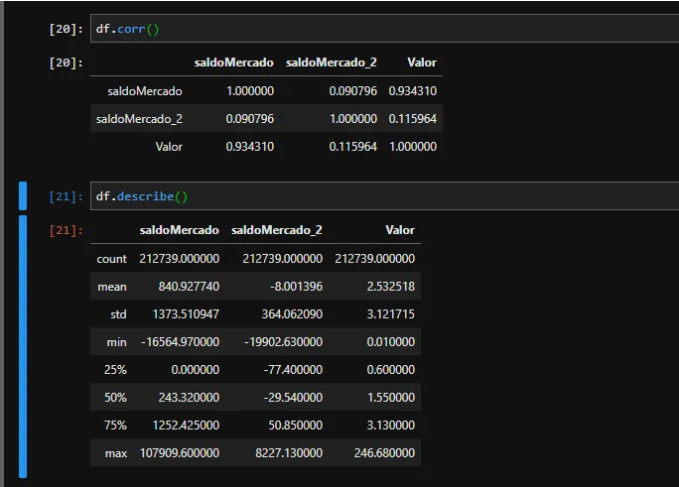
Préparation du modèle

Nous préparons nos valeurs pour le modèle d'apprentissage automatique en définissant les variables prédictives et la variable que nous voulons prédire. Nous utilisons train_test_split pour diviser aléatoirement les données en 30 % pour les tests et 70 % pour la formation.

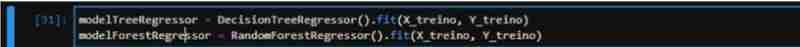
Enfin, nous initialisons les deux algorithmes (RandomForest et DecisionTree), ajustons les données et mesurons le score des deux avec les données de test. Nous avons obtenu un score de 83 % pour TreeRegressor et de 90 % pour ForestRegressor, ce qui indique en théorie que ForestRegressor a mieux performé.

Résultats et analyse

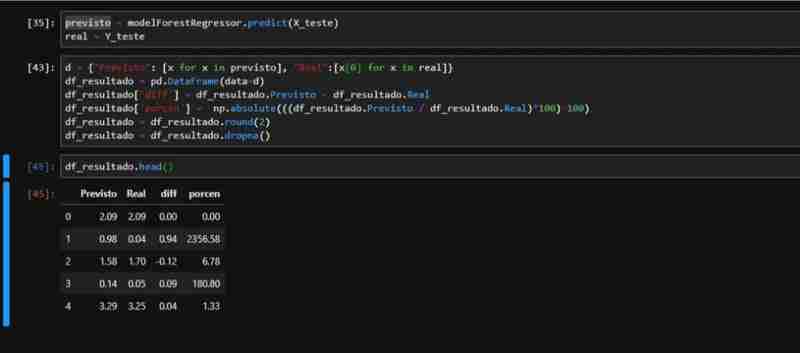
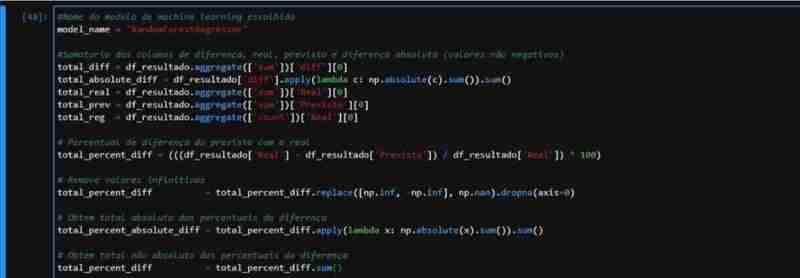
Compte tenu des performances partiellement observées de ForestRegressor, nous avons créé un ensemble de données avec les données nécessaires pour appliquer les métriques. Nous effectuons la prédiction sur les données de test et créons un DataFrame avec les valeurs réelles et prédites, y compris les colonnes de différence et de pourcentage.

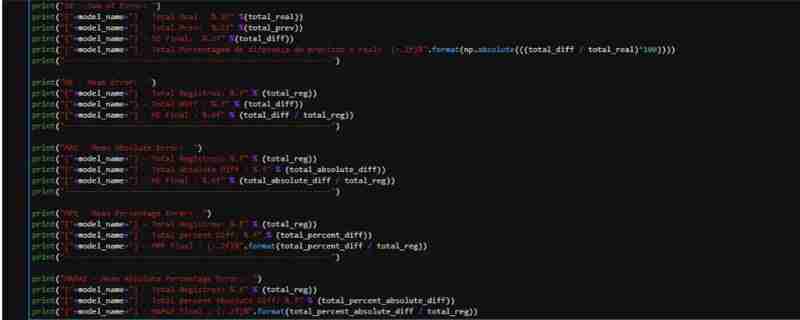
Nous pouvons observer que par rapport au total réel du taux du dollar par rapport au taux prédit par notre modèle :

• Nous avons eu une différence totale de 578,00 R$
• Cela représente une différence de 0,36 % entre les valeurs prédites et réelles (non considérées comme des valeurs absolues)
• En termes d'erreur moyenne (ME), nous avions une faible valeur, une moyenne de 0,009058 R$
• Pour la moyenne absolue, cette valeur augmente un peu, puisque nous avons des valeurs négatives dans notre ensemble de données

Je souligne qu'ici nous effectuons le calcul manuellement à des fins pédagogiques. Cependant, il est recommandé d'utiliser les fonctions de métriques du package Sklearn en raison de meilleures performances et du faible risque d'erreur dans le calcul.

Le code complet est disponible sur mon GitHub : github.com/AirtonLira/artigo_metricasregressao

---

Auteur : Airton Lira Junior

LinkedIn : linkedin.com/in/airton-lira-junior-6b81a661/

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!