Insérer les plus grands diviseurs communs dans la liste chaînée

2807. Insérer les plus grands diviseurs communs dans la liste chaînée

Difficulté :Moyen

Sujets : Liste chaînée, mathématiques, théorie des nombres

Étant donné l'en-tête d'un en-tête de liste chaînée, dans lequel chaque nœud contient une valeur entière.

Entre chaque paire de nœuds adjacents, insérez un nouveau nœud avec une valeur égale au plus grand diviseur commun d'entre eux.

Renvoyer la liste chaînée après insertion.

Le plus grand diviseur commun de deux nombres est le plus grand entier positif qui divise uniformément les deux nombres.

Exemple 1 :

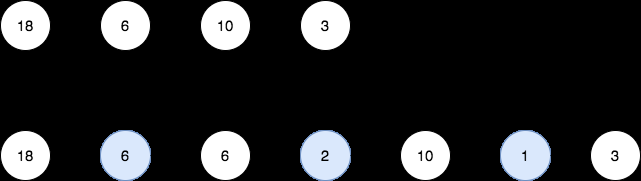
• Entrée : tête = [18,6,10,3]
• Sortie : [18,6,6,2,10,1,3]
• Explication : Le 1^st diagramme désigne la liste chaînée initiale et le 2^ème diagramme désigne la liste chaînée après avoir inséré les nouveaux nœuds (les nœuds en bleu sont les nœuds insérés nœuds).
  • On insère le plus grand commun diviseur de 18 et 6 = 6 entre le 1^er et le 2^ème nœuds.
  • On insère le plus grand commun diviseur de 6 et 10 = 2 entre le 2^ème et le 3^ème nœuds.
  • On insère le plus grand commun diviseur de 10 et 3 = 1 entre le 3^ème et le 4^ème nœuds. Il n'y a plus de nœuds adjacents, nous renvoyons donc la liste chaînée.

Exemple 2 :

• Entrée : head = [7]
• Sortie : [7]
• Explication : Le 1^st diagramme désigne la liste chaînée initiale et le 2^ème diagramme désigne la liste chaînée après avoir inséré les nouveaux nœuds. Il n'y a pas de paires de nœuds adjacents, nous renvoyons donc la liste chaînée initiale.

Exemple 3 :

• Entrée : coût = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
• Sortie : 10

Contraintes :

• Le nombre de nœuds dans la liste est compris entre [1, 5000].
• 1 <= Node.val <= 1000

Indice :

1. Chaque point de gauche serait soit connecté exactement à un point déjà connecté à un nœud de gauche, soit à un sous-ensemble de nœuds de droite qui ne sont connectés à aucun nœud
2. Utilisez la programmation dynamique avec masquage de bits, où sera l'état (nombre de points attribués dans le premier groupe, masque de points attribués dans le deuxième groupe).

Solution :

Nous devons insérer des nœuds entre chaque paire de nœuds adjacents dans une liste chaînée. La valeur du nœud inséré doit être le plus grand diviseur commun (PGCD) des valeurs des deux nœuds adjacents. Nous allons parcourir la liste chaînée, calculer le GCD pour chaque paire de nœuds adjacents, puis insérer le nouveau nœud en conséquence.

Voici comment vous pouvez aborder cela :

1. Définir une classe ListNode : Cette classe représentera chaque nœud de la liste chaînée.
2. Parcourir la liste : nous parcourrons la liste pour trouver chaque paire de nœuds adjacents.
3. Insérer des nœuds GCD : Pour chaque paire de nœuds adjacents, nous insérerons un nouveau nœud dont la valeur est le GCD des deux nœuds adjacents.
4. Renvoyer la liste modifiée.

Implémentons cette solution en PHP : 2807. Insérer les plus grands diviseurs communs dans la liste chaînée

<?php
// Definition for a singly-linked list node.
class ListNode {
    public $val = 0;
    public $next = null;

    public function __construct($val = 0, $next = null) {
        $this->val = $val;
        $this->next = $next;
    }
}

/**
 * Function to calculate the GCD of two numbers.
 *
 * @param $a
 * @param $b
 * @return mixed
 */
function gcd($a, $b) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */

}

/**
 * @param ListNode $head
 * @return ListNode
 */
function insertGreatestCommonDivisors($head) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * Function to print the linked list for testing purposes.
 * 
 * @param $head
 * @return void
 */
function printList($head) {
    $current = $head;
    while ($current != null) {
        echo $current->val . " ";
        $current = $current->next;
    }
    echo "\n";
}

// Example usage:

// Create the linked list: 18 -> 6 -> 10 -> 3
$head = new ListNode(18);
$head->next = new ListNode(6);
$head->next->next = new ListNode(10);
$head->next->next->next = new ListNode(3);

// Insert GCD nodes.
$modifiedHead = insertGreatestCommonDivisors($head);

// Print the modified linked list.
printList($modifiedHead);

// Output should be: 18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3
?>




<h3>
  
  
  Explication:
</h3>

<ol>
<li><p><strong>Classe ListNode</strong> : Cette classe représente la structure d'un nœud dans la liste chaînée, avec des propriétés pour la valeur ($val) et le nœud suivant ($next).</p></li>
<li><p><strong>Calcul GCD</strong> : La fonction pgcd utilise l'algorithme euclidien pour calculer le plus grand diviseur commun de deux entiers.</p></li>
<li>
<p><strong>Logique principale (insertGreatestCommonDivisors)</strong> :</p>

<ul>
<li>Nous parcourons la liste chaînée jusqu'à ce que nous atteignions l'avant-dernier nœud.</li>
<li>Pour chaque paire de nœuds adjacents, nous calculons le PGCD de leurs valeurs.</li>
<li>Nous créons un nouveau nœud avec cette valeur GCD et l'insérons entre le nœud actuel et le nœud suivant.</li>
</ul>
</li>
<li><p><strong>Edge Case</strong> : Si la liste n'a qu'un seul nœud, nous le renvoyons tel quel sans apporter de modifications puisqu'il n'y a pas de nœuds adjacents.</p></li>
<li><p><strong>Test</strong> : La fonction printList est une fonction d'assistance utilisée pour afficher les valeurs de la liste chaînée pour vérification.</p></li>
</ol>

<h3>
  
  
  Time Complexity:
</h3>

<ul>
<li>The time complexity of this solution is (O(n)), where (n) is the number of nodes in the linked list. Calculating the GCD for each adjacent pair takes constant time on average, and we perform a linear traversal of the list.</li>
</ul>

<h3>
  
  
  Example:
</h3>

<p>For the input list [18, 6, 10, 3], the output is:<br>
</p>

<pre class="brush:php;toolbar:false">18 -> 6 -> 6 -> 2 -> 10 -> 1 -> 3

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!