Maison >Java >javaDidacticiel >Graphiques et applications pondérés
Graphiques et applications pondérés
- 王林original
- 2024-09-06 06:06:22808parcourir
Un graphique est un graphique pondéré si chaque arête se voit attribuer un poids. Les graphiques pondérés ont de nombreuses applications pratiques.
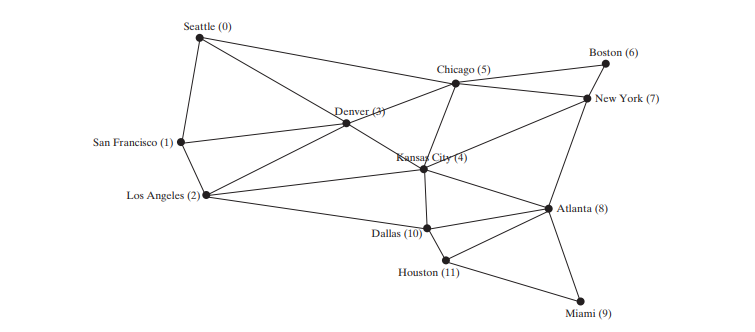
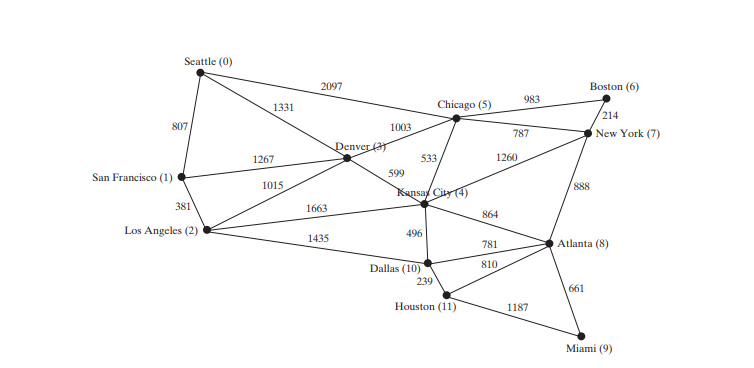
La figure ci-dessus suppose que le graphique représente le nombre de vols entre les villes. Vous pouvez appliquer le BFS pour trouver le moins de vols entre deux villes. Supposons que les bords représentent les distances de conduite entre les villes, comme le montre la figure ci-dessous. Comment trouver les distances totales minimales pour relier toutes les villes ? Comment trouver le chemin le plus court entre deux villes ? Ce chapitre répondra à ces questions. Le premier est connu sous le nom de problème de l'arbre couvrant minimum (MST) et le second sous le nom de problème du chemin le plus court.
Le chapitre précédent a introduit la notion de graphiques. Vous avez appris à représenter des arêtes à l'aide de tableaux d'arêtes, de listes d'arêtes, de matrices de contiguïté et de listes de contiguïté, et à modéliser un graphique à l'aide de l'interface Graph, de la classe AbstractGraph et de la classe AbstractGraph. 🎜>Classe UnweightedGraph
. Le chapitre précédent a également présenté deux techniques importantes pour parcourir des graphiques : la recherche en profondeur d'abord et la recherche en largeur d'abord, et le parcours appliqué pour résoudre des problèmes pratiques. Les articles suivants présenteront des graphiques pondérés. Vous apprendrez l'algorithme pour trouver un arbre couvrant minimum en post et l'algorithme pour trouver les chemins les plus courts en post.Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Comment dessiner des rectangles de manière permanente dans un JPanel : utiliser BufferedImages pour éviter l'écrasement ?
- Comment implémenter la comparaison de chaînes d'ordre de tri naturel en Java ?
- Propriétés Kotlin et champs Java : une histoire de deux variables (où Kotlin a plus d'astuces dans sa manche !)
- Comment résoudre le problème « javax.xml.bind » dans Java 11 ?
- Comment calculer les jours entre les dates dans Java 8, en gérant l'heure d'été et les objets de date ?

