Maison >Java >javaDidacticiel >La classe WeightedGraph
La classe WeightedGraph
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBoriginal
- 2024-09-06 06:01:02794parcourir
La classe WeightedGraph étend AbstractGraph.
Le chapitre précédent a conçu l'interface Graph, la classe AbstractGraph et la classe UnweightedGraph pour la modélisation de graphiques. En suivant ce modèle, nous concevons WeightedGraph comme une sous-classe de AbstractGraph, comme le montre la figure ci-dessous.

WeightedGraph étend simplement AbstractGraph avec cinq constructeurs pour créer des instances concrètes de WeightedGraph. WeightedGraph hérite de toutes les méthodes de AbstractGraph, remplace les méthodes clear et addVertex, implémente une nouvelle méthode addEdge pour en ajoutant un bord pondéré, et introduit également de nouvelles méthodes pour obtenir des arbres couvrant minimum et pour trouver tous les chemins les plus courts à partir d'une source unique. Les arbres couvrant minimum et les chemins les plus courts seront introduits respectivement dans les sections Arbres couvrant minimum et chemins les plus courts.
Le code ci-dessous implémente WeightedGraph. Les listes de contiguïté d'arêtes (lignes 38 à 63) sont utilisées en interne pour stocker les arêtes adjacentes d'un sommet. Lorsqu'un WeightedGraph est construit, ses listes de contiguïté de bords sont créées (lignes 47 et 57). Les méthodes getMinimumSpanningTree() (lignes 99 à 138) et getShortestPath() (lignes 156 à 197) seront présentées dans les prochaines sections.
package demo;
import java.util.*;
public class WeightedGraph<V> extends AbstractGraph<V> {
/** Construct an empty */
public WeightedGraph() {}
/** Construct a WeightedGraph from vertices and edged in arrays */
public WeightedGraph(V[] vertices, int[][] edges) {
createWeightedGraph(java.util.Arrays.asList(vertices), edges);
}
/** Construct a WeightedGraph from vertices and edges in list */
public WeightedGraph(int[][] edges, int numberOfVertices) {
List<V> vertices = new ArrayList<>();
for (int i = 0; i < numberOfVertices; i++)
vertices.add((V)(new Integer(i)));
createWeightedGraph(vertices, edges);
}
/** Construct a WeightedGraph for vertices 0, 1, 2 and edge list */
public WeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
createWeightedGraph(vertices, edges);
}
/** Construct a WeightedGraph from vertices 0, 1, and edge array */
public WeightedGraph(List<WeightedEdge> edges, int numberOfVertices) {
List<V> vertices = new ArrayList<>();
for (int i = 0; i < numberOfVertices; i++)
vertices.add((V)(new Integer(i)));
createWeightedGraph(vertices, edges);
}
/** Create adjacency lists from edge arrays */
private void createWeightedGraph(List<V> vertices, int[][] edges) {
this.vertices = vertices;
for (int i = 0; i < vertices.size(); i++) {
neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
}
for (int i = 0; i < edges.length; i++) {
neighbors.get(edges[i][0]).add(new WeightedEdge(edges[i][0], edges[i][1], edges[i][2]));
}
}
/** Create adjacency lists from edge lists */
private void createWeightedGraph(List<V> vertices, List<WeightedEdge> edges) {
this.vertices = vertices;
for (int i = 0; i < vertices.size(); i++) {
neighbors.add(new ArrayList<Edge>()); // Create a list for vertices
}
for (WeightedEdge edge: edges) {
neighbors.get(edge.u).add(edge); // Add an edge into the list
}
}
/** Return the weight on the edge (u, v) */
public double getWeight(int u, int v) throws Exception {
for (Edge edge : neighbors.get(u)) {
if (edge.v == v) {
return ((WeightedEdge)edge).weight;
}
}
throw new Exception("Edge does not exit");
}
/** Display edges with weights */
public void printWeightedEdges() {
for (int i = 0; i < getSize(); i++) {
System.out.print(getVertex(i) + " (" + i + "): ");
for (Edge edge : neighbors.get(i)) {
System.out.print("(" + edge.u + ", " + edge.v + ", " + ((WeightedEdge)edge).weight + ") ");
}
System.out.println();
}
}
/** Add edges to the weighted graph */
public boolean addEdge(int u, int v, double weight) {
return addEdge(new WeightedEdge(u, v, weight));
}
/** Get a minimum spanning tree rooted at vertex 0 */
public MST getMinimumSpanningTree() {
return getMinimumSpanningTree(0);
}
/** Get a minimum spanning tree rooted at a specified vertex */
public MST getMinimumSpanningTree(int startingVertex) {
// cost[v] stores the cost by adding v to the tree
double[] cost = new double[getSize()];
for (int i = 0; i < cost.length; i++) {
cost[i] = Double.POSITIVE_INFINITY; // Initial cost
}
cost[startingVertex] = 0; // Cost of source is 0
int[] parent = new int[getSize()]; // Parent of a vertex
parent[startingVertex] = -1; // startingVertex is the root
double totalWeight = 0; // Total weight of the tree thus far
List<Integer> T = new ArrayList<>();
// Expand T
while (T.size() < getSize()) {
// Find smallest cost v in V - T
int u = -1; // Vertex to be determined
double currentMinCost = Double.POSITIVE_INFINITY;
for (int i = 0; i < getSize(); i++) {
if (!T.contains(i) && cost[i] < currentMinCost) {
currentMinCost = cost[i];
u = i;
}
}
T.add(u); // Add a new vertex to T
totalWeight += cost[u]; // Add cost[u] to the tree
// Adjust cost[v] for v that is adjacent to u and v in V - T
for (Edge e : neighbors.get(u)) {
if (!T.contains(e.v) && cost[e.v] > ((WeightedEdge)e).weight) {
cost[e.v] = ((WeightedEdge)e).weight;
parent[e.v] = u;
}
}
} // End of while
return new MST(startingVertex, parent, T, totalWeight);
}
/** MST is an inner class in WeightedGraph */
public class MST extends Tree {
private double totalWeight; // Total weight of all edges in the tree
public MST(int root, int[] parent, List<Integer> searchOrder, double totalWeight) {
super(root, parent, searchOrder);
this.totalWeight = totalWeight;
}
public double getTotalWeight() {
return totalWeight;
}
}
/** Find single source shortest paths */
public ShortestPathTree getShortestPath(int sourceVertex) {
// cost[v] stores the cost of the path from v to the source
double[] cost = new double[getSize()];
for (int i = 0; i < cost.length; i++) {
cost[i] = Double.POSITIVE_INFINITY; // Initial cost set to infinity
}
cost[sourceVertex] = 0; // Cost of source is 0
// parent[v] stores the previous vertex of v in the path
int[] parent = new int[getSize()];
parent[sourceVertex] = -1; // The parent of source is set to -1
// T stores the vertices whose path found so far
List<Integer> T = new ArrayList<>();
// Expand T
while (T.size() < getSize()) {
// Find smallest cost v in V - T
int u = -1; // Vertex to be determined
double currentMinCost = Double.POSITIVE_INFINITY;
for (int i = 0; i < getSize(); i++) {
if (!T.contains(i) && cost[i] < currentMinCost) {
currentMinCost = cost[i];
u = i;
}
}
T.add(u); // Add a new vertex to T
// Adjust cost[v] for v that is adjacent to u and v in V - T
for (Edge e : neighbors.get(u)) {
if (!T.contains(e.v) && cost[e.v] > cost[u] + ((WeightedEdge)e).weight) {
cost[e.v] = cost[u] + ((WeightedEdge)e).weight;
parent[e.v] = u;
}
}
} // End of while
// Create a ShortestPathTree
return new ShortestPathTree(sourceVertex, parent, T, cost);
}
/** ShortestPathTree is an inner class in WeightedGraph */
public class ShortestPathTree extends Tree {
private double[] cost; // cost[v] is the cost from v to source
/** Construct a path */
public ShortestPathTree(int source, int[] parent, List<Integer> searchOrder, double[] cost) {
super(source, parent, searchOrder);
this.cost = cost;
}
/** Return the cost for a path from the root to vertex v */
public double getCost(int v) {
return cost[v];
}
/** Print paths from all vertices to the source */
public void printAllPaths() {
System.out.println("All shortest paths from " + vertices.get(getRoot()) + " are:");
for (int i = 0; i < cost.length; i++) {
printPath(i); // Print a path from i to the source
System.out.println("(cost: " + cost[i] + ")"); // Path cost
}
}
}
}
La classe WeightedGraph étend la classe AbstractGraph (ligne 3). Les propriétés vertices et neighbours dans AbstractGraph sont héritées dans WeightedGraph.neighbors est une liste. Chaque élément est la liste est une autre liste qui contient des arêtes. Pour un graphique non pondéré, chaque arête est une instance de AbstractGraph.Edge. Pour un graphique pondéré, chaque arête est une instance de WeightedEdge. WeightedEdge est un sous-type de Edge. Vous pouvez donc ajouter une arête pondérée dans neighbours.get(i) pour un graphique pondéré (ligne 47).
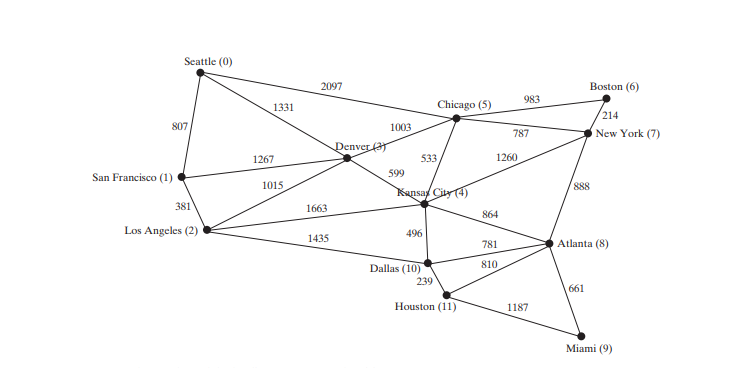
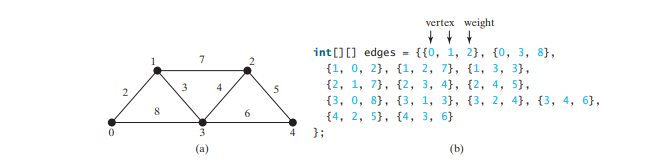
Le code ci-dessous donne un programme de test qui crée un graphique pour celui de la figure ci-dessous et un autre graphique pour celui de la figure ci-dessous a.
package demo;
public class TestWeightedGraph {
public static void main(String[] args) {
String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};
int[][] edges = {
{0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
{1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
{2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
{3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
{4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
{5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
{6, 5, 983}, {6, 7, 214},
{7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
{8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
{9, 8, 661}, {9, 11, 1187},
{10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
{11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
};
WeightedGraph<String> graph1 = new WeightedGraph<>(vertices, edges);
System.out.println("The number of vertices in graph1: " + graph1.getSize());
System.out.println("The vertex with index 1 is " + graph1.getVertex(1));
System.out.println("The index for Miami is " + graph1.getIndex("Miami"));
System.out.println("The edges for graph1:");
graph1.printWeightedEdges();
edges = new int[][] {
{0, 1, 2}, {0, 3, 8},
{1, 0, 2}, {1, 2, 7}, {1, 3, 3},
{2, 1, 7}, {2, 3, 4}, {2, 4, 5},
{3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
{4, 2, 5}, {4, 3, 6}
};
WeightedGraph<Integer> graph2 = new WeightedGraph<>(edges, 5);
System.out.println("\nThe edges for graph2:");
graph2.printWeightedEdges();
}
}
Le nombre de sommets dans le graphique 1 : 12
Le sommet d'indice 1 est San Francisco
L'indice pour Miami est 9
Les arêtes du graphique 1 :
Sommet 0 : (0, 1, 807) (0, 3, 1331) (0, 5, 2097)
Sommet 1 : (1, 2, 381) (1, 0, 807) (1, 3, 1267)
Sommet 2 : (2, 1, 381) (2, 3, 1015) (2, 4, 1663) (2, 10, 1435)
Sommet 3 : (3, 4, 599) (3, 5, 1003) (3, 1, 1267)
(3, 0, 1331) (3, 2, 1015)
Sommet 4 : (4, 10, 496) (4, 8, 864) (4, 5, 533) (4, 2, 1663)
(4, 7, 1260) (4, 3, 599)
Sommet 5 : (5, 4, 533) (5, 7, 787) (5, 3, 1003)
(5, 0, 2097) (5, 6, 983)
Sommet 6 : (6, 7, 214) (6, 5, 983)
Sommet 7 : (7, 6, 214) (7, 8, 888) (7, 5, 787) (7, 4, 1260)
Sommet 8 : (8, 9, 661) (8, 10, 781) (8, 4, 864)
(8, 7, 888) (8, 11, 810)
Sommet 9 : (9, 8, 661) (9, 11, 1187)
Sommet 10 : (10, 11, 239) (10, 4, 496) (10, 8, 781) (10, 2, 1435)
Sommet 11 : (11, 10, 239) (11, 9, 1187) (11, 8, 810)
Les arêtes du graphique2 :
Sommet 0 : (0, 1, 2) (0, 3, 8)
Sommet 1 : (1, 0, 2) (1, 2, 7) (1, 3, 3)
Sommet 2 : (2, 3, 4) (2, 1, 7) (2, 4, 5)
Sommet 3 : (3, 1, 3) (3, 4, 6) (3, 2, 4) (3, 0, 8)
Sommet 4 : (4, 2, 5) (4, 3, 6)
Le programme crée graph1 pour le graphique de la figure ci-dessus, lignes 3 à 27. Les sommets de graph1 sont définis dans les lignes 3 à 5. Les bords du graph1 sont définis aux lignes 7 à 24. Les bords sont représentés à l'aide d'un tableau bidimensionnel. Pour chaque ligne i du tableau, edges[i][0] et edges[i][1] indiquent qu'il y a une arête à partir du sommet edges[i] [0] au sommet edges[i][1] et le poids du bord est edges[i][2]. Par exemple, {0, 1, 807} (ligne 8) représente l'arête du sommet 0 (arêtes[ 0][0]) au sommet 1 (edges[0][1]) avec un poids 807 (edges[0] [2]). {0, 5, 2097} (ligne 8) représente l'arête du sommet 0 (edges[2][ 0]) au sommet 5 (arêtes[2][1]) avec un poids 2097 (arêtes[2][2] ). La ligne 35 appelle la méthode printWeightedEdges() sur graph1 pour afficher toutes les arêtes dans graph1.
Le programme crée les arêtes pour graph2 pour le graphique de la figure ci-dessus a aux lignes 37 à 44. La ligne 46 appelle la méthode printWeightedEdges() sur graph2 pour afficher toutes les arêtes dans graph2.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

