Coût minimum pour connecter deux groupes de points

1595. Coût minimum pour connecter deux groupes de points

Difficulté : Difficile

Sujets : Tableau, programmation dynamique, manipulation de bits, matrice, masque de bits

Vous recevez deux groupes de points où le premier groupe a une taille₁ points, le deuxième groupe a une taille₂ points et une taille₁ > = taille₂.

Le coût de la connexion entre deux points quelconques est donné dans une matrice taille₁ x taille₂ où coût[i][j] est le coût de connexion du point i de le premier groupe et le point j du deuxième groupe. Les groupes sont connectés si chaque point des deux groupes est connecté à un ou plusieurs points du groupe opposé. Autrement dit, chaque point du premier groupe doit être connecté à au moins un point du deuxième groupe, et chaque point du deuxième groupe doit être connecté à au moins un point du premier groupe.

Renvoyer le coût minimum nécessaire pour connecter les deux groupes.

Exemple 1 :

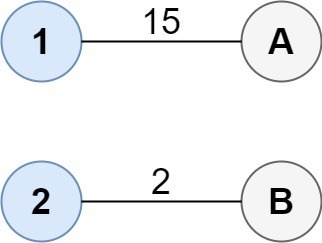
• Entrée : coût = [[15, 96], [36, 2]]
• Sortie : 17
• Explication : La manière optimale de connecter les groupes est :

  1--A
  2--B
  This results in a total cost of 17.

Exemple 2 :

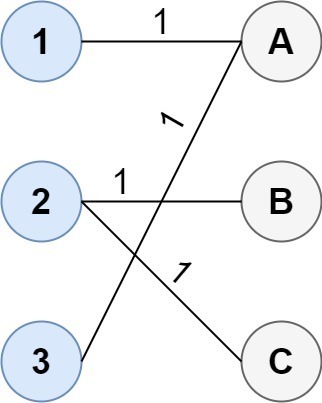
• Entrée : coût = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
• Sortie : 4
• Explication : La manière optimale de connecter les groupes est :

  1--A
  2--B
  2--C
  3--A
  This results in a total cost of 4.

Notez qu'il y a plusieurs points connectés au point 2 dans le premier groupe et au point A dans le deuxième groupe. Cela n’a pas d’importance car il n’y a pas de limite au nombre de points pouvant être connectés. Nous ne nous soucions que du coût total minimum.

Exemple 3 :

• Entrée : coût = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8] ]
• Sortie : 10

Contraintes :

• taille₁ == coût.longueur
• taille₂ == coût[i].longueur
• 1 <= taille₁, taille₂ <= 12
• taille₁ >= taille₂
• 0 <= coût[i][j] <= 100

Indice :

1. Chaque point de gauche serait soit connecté exactement à un point déjà connecté à un nœud de gauche, soit à un sous-ensemble de nœuds de droite qui ne sont connectés à aucun nœud
2. Utilisez la programmation dynamique avec masquage de bits, où sera l'état (nombre de points attribués dans le premier groupe, masque de points attribués dans le deuxième groupe).

Solution :

Nous pouvons tirer parti de la programmation dynamique avec le masquage de bits. L'idée est de minimiser le coût en considérant chaque point du premier groupe et en essayant de le connecter à tous les points du deuxième groupe.

Approche de programmation dynamique (DP) avec masquage de bits

Mesures:

1. Représentation de l'État :

   • Utilisez une table DP dp[i][mask] où :
     • i est l'index du premier groupe (allant de 0 à size1-1).
     • Le masque est un masque de bits représentant les points du deuxième groupe qui ont été connectés.

2. Transition d'État :

   • Pour chaque point du premier groupe, essayez de le connecter à chaque point du deuxième groupe, en mettant à jour le tableau DP en conséquence.
   • Si un nouveau point du deuxième groupe est connecté, mettre à jour le bit correspondant dans le masque.

3. Cas de base :

   • Commencez avec dp[0][0] = 0 (aucune connexion initialement).

4. Objectif :

   • Calculez le coût minimum pour dp[size1][(1 << size2) - 1], qui représente la connexion de tous les points des deux groupes.

Implémentons cette solution en PHP : 1595. Coût minimum pour connecter deux groupes de points

  
  
  Explication:



Le tableau DP dp[i][mask] stocke le coût minimum pour connecter les i premiers points du groupe 1 avec les points du groupe 2 comme indiqué par le masque.
Les boucles imbriquées parcourent chaque combinaison de i et de masque, en essayant de trouver le coût optimal en considérant toutes les connexions possibles.
Au final, la solution calcule le coût minimum en tenant compte des scénarios dans lesquels certains points du deuxième groupe peuvent encore être déconnectés, garantissant ainsi que tous les points sont connectés.


Cette approche gère efficacement les contraintes du problème et garantit le coût minimum de connexion des deux groupes.

Liens de contact
Si vous avez trouvé cette série utile, pensez à donner une étoile au référentiel sur GitHub ou à partager la publication sur vos réseaux sociaux préférés ?. Votre soutien signifierait beaucoup pour moi !

Si vous souhaitez du contenu plus utile comme celui-ci, n'hésitez pas à me suivre :


LinkedIn
GitHub



          

            
        
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!