Série de Fibonacci en Java

La série de Fibonacci réside dans le processus selon lequel chaque nombre agit comme une somme de deux valeurs précédentes et la séquence commence toujours par les entiers de base 0 et 1. Les nombres de Fibonacci sont musculairement liés au nombre d'or. Dans cette rubrique, nous allons voir la série de Fibonacci en Java.

Commencez votre cours de développement de logiciels libres

Développement Web, langages de programmation, tests de logiciels et autres

Formule :

un = un − 2 + un − 1

Fibonacci series for first 21 numbers
F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16	F17	F18	F19	F20
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765

Série de Fibonacci pour les 21 premiers nombres

F₀

F₁

F₂

F₃

F₄

F₅

F₆

F₇

F₈

F₉

F₁₀

F₁₁

F₁₂

F₁₃

F₁₄

F₁₅

F₁₆

F₁₇

F₁₈

F₁₉

F₂₀

0

1

1

2

3

5

8

13

21

34

55

89

144

233

377

610

987

1597

2584

4181

6765

Applications clés

Voici les applications clés de la série Fibonacci en Java ci-dessous :

• Conversion de miles en kilomètres et de kilomètres en miles.
• Quelques exemples de méthodologie Agile.
• Le calcul de l'analyse du temps d'exécution de l'algorithme d'Euclide est effectué à l'aide de cette technique de série.
• Les statistiques de Fibonacci sont utilisées mathématiquement par certains générateurs de nombres pseudo-aléatoires.
• Le processus de planification du poker implique l'utilisation de cette technique.
• La technique de structure des données du tas de Fibonacci est réalisée à l'aide de la technique des séries de Fibonacci.
• En optique, tandis qu'un rayon de lumière brille à un point de vue du début à la fin de deux plaques translucides empilées de matériaux différents et d'indices de réfraction différents, il peut renvoyer sur trois surfaces : le sommet, le centre et les surfaces de base de les deux assiettes. Le chiffre du chemin de rayon différent pour avoir kréflexions, pour k > 1, est le {style d'affichage k} le nombre de Fibonacci.

Programme série Fibonacci (programme non récursif)

Voici un programme de série de Fibonacci :

Code :

// Fibonacci series program
public class Fibonacci {
// main program
public static void main(String[] args) {
int count = 10, var1 = 0, var2 = 1;
System.out.print("First " + count + " terms: ");
// Fibonacci series formation loop
for (int i = 1; i <= count; ++i)
{
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
}
}
}

Sortie :

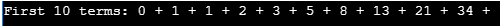
Explication :

• Ce programme calcule la série de Fibonacci pour une plage de nombres donnée.
• Ici, ce processus est réalisé sans technique récursive.

Algorithme du programme

• Une classe racine Fibonacci est déclarée avec la nécessité que tous les codes de programme intégrés dans cette classe abordent la fonctionnalité permettant d'obtenir une série de nombres Fibonacci.
• Dans la classe racine, la méthode main est déclarée. La méthode main agit, en règle générale, comme une méthode Java significative. L'exécution de la JVM n'aura pas lieu sans la présence de la méthode main dans le programme. L'explication des différents sous-composants de la méthode principale est exprimée ci-dessous,
• Ensuite, la section d'initialisation des variables est implicite. Cette section implique l'initialisation de trois variables différentes. Deux d'entre elles servent à réaliser la logique de Fibonacci via un échange de valeurs de niveau variable, et une autre variable est appliquée pour réguler le nombre de valeurs pour lesquelles la logique de Fibonacci doit être générée.
• La logique clé du programme de la série Fibonacci est obtenue à l'aide de la boucle for ci-dessous dans la section programme.

Code :

for (int i = 1; i <= count; ++i)
{
System.out.print(var1 + " + ");
int added_sum= var1 + var2;
var1 = var2;
var2 = added_sum;
}

• La logique derrière cela pour la section boucle est la suivante ; initialement, une plage de valeurs est exécutée sur une boucle ; la boucle se produit avec un incrément sur la valeur de plage pour chaque flux. De plus, dans chaque flux, la valeur des deux variables d'échange est résumée dans une troisième variable.
• Après le résumé, la deuxième valeur de la variable est implicite dans la première variable, ce qui fait que la première valeur de la variable est éliminée de ce processus. À l'étape suivante, la valeur additionnée est attribuée à la deuxième variable.

Donc à la fin de cette instance, pour un seul flux logique, les événements ci-dessous sont appliqués :

• La valeur de la première variable est effacée.
• La valeur de la deuxième variable existante est renseignée dans la première variable.
• La valeur résumée est déplacée dans la deuxième variable.

En effectuant la séquence logique ci-dessous pour le nombre de valeurs donné nécessaire, la série de Fibonacci peut être obtenue.

1. Programme de la série Fibonacci (utilisation de tableaux)

Code :

import java.util.Arrays;
public class Main {
public static void main(String[] args) {
int Count = 15;
long[] array = new long[Count];
array[0] = 0;
array[1] = 1;
for (int x = 2; x < Count; x++) {
array[x] = array[x - 1] + array[x - 2];
}
System.out.print(Arrays.toString(array));
}
}

Sortie  :

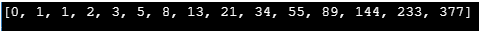
Explication :

•  Impliquant la logique du programme rédigée ci-dessus, mais dans ce cas, les entrées de Fibonacci sont stockées dans le cadre de tableaux.
• Ainsi toutes les opérations mentionnées ci-dessus sont réalisées concernant un tableau.

2. Programme de la série Fibonacci (sans impliquer de boucles)

Code :

public class Fibonaccifunction
{
private static int indexvalue = 0;
private static int endPoint = 9;
public static void main (String[] args)
{
int number1 = 0;
int number2 = 1;
fibonaccifunction(number1, number2);
}
public static void fibonaccifunction(int number1, int number2)
{
System.out.println("index value : " + indexvalue + " -> " + number1);
if (indexvalue == endPoint)
return;
indexvalue++;
fibonaccifunction(number2, number1+number2);
}
}

Sortie  :

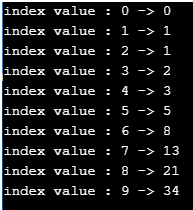
Explication :

•  Impliquant la logique du programme rédigée ci-dessus mais dans ce cas, les entrées de Fibonacci sont traitées de manière récursive à l'aide d'une fonction nommée Fibonacci.

3. Programme de la série Fibonacci (sans impliquer de boucles mais réalisé uniquement en utilisant des conditions)

Code :

public class Fibonacci_with_conditions
{
static int number2=1;
static int number1=0;
static int next=0;
public static  void Fibonacci_conditions( int number)
{
if(number<10)
{
if(number == 0)
{
System.out.print(" "+number);
number++;
Fibonacci_conditions (number);
}
else
if(number == 1)
{
System.out.print(" "+number);
number++;
Fibonacci_conditions(number);
}
else{
next=number1+number2;
System.out.print(" "+next);
number1=number2;
number2=next;
number++;
Fibonacci_conditions(number);
}
}
}
public static void main(String[] args)
{
Fibonacci_conditions(0);
}
}

Sortie :

Explication :

• Implying the program logic drafted above, but at this instance, the Fibonacci inputs are regulated only through necessary conditional statements.
• According to the conditions, the swapping of the variables is necessarily carried out.

4. Fibonacci Series Program( Without Loops, the Concepts of Looping is Achieved using Nextint Method)

Code:

import java.util.*;
public class Fibonacci_series
{
public static void main(String[] args)
{
System.out.println("Input:");
int number= 10,value1=1,value2=0,value3=0;
num(number, value1, value2, value3);
}
public static void num(int number,int value1,int value2,int value3)
{
if(value1 <= number)
{
System.out.println(value1);
value3=value2;
value2=value1;
value1=value2+value3;
num(number,value1,value2,value3);
}
}
}

Output:

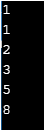
Explanation:

• Implying the program logic drafted above, but at this instance, the Fibonacci inputs are handled recursively using a function named num, and the loop is carried out using the nextInt function.

Conclusion – Fibonacci Series in Java

These programs are implied to achieve the Fibonacci series for a given integer value.  A largely classified set of techniques are implied in the given list of examples. Techniques like an array-oriented approach and a condition-alone approach are very much peculiar.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!