Maison >Java >javaDidacticiel >Récursivité en Java
Récursivité en Java
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBoriginal
- 2024-08-30 15:33:33447parcourir
La récursion en Java est définie comme « une méthode s'appelle elle-même (même méthode) en continu, directement ou indirectement ». Une fonction de récursivité est utilisée dans les situations où le même ensemble d'opérations doit être effectué encore et encore jusqu'à ce que le résultat soit atteint. Il effectue plusieurs itérations et l’énoncé du problème devient de plus en plus simple à chaque itération. La récursion en Java est une méthode de résolution de problème basée sur la solution du plus petit bloc du même problème. La plupart des itérations aux possibilités infinies peuvent être résolues par récursion. Nous pouvons dire que la récursion est une méthode alternative aux instructions en boucle. Si nous n'avons pas utilisé correctement la fonction récursive, alors elle s'exécute des temps infinis.
Syntaxe :
PUBLICITÉ Cours populaire dans cette catégorie MAÎTRISÉE JAVA - Spécialisation | 78 séries de cours | 15 tests simulésreturntype methodName()
{
//logic for application
methodName();//recursive call
}
Comment pouvons-nous arrêter les conditions infinies de récursion en Java ?
Pour arrêter les conditions infinies, nous devons avoir ce qui suit :
- Condition de base : Précisez à l'intérieur si la condition devait arrêter la fonction de récursivité.
- Appel récursif : Appel récursif approprié.
On peut appeler une fonction de récursivité de 2 manières :
1. Appel de récursion directe
Si nous appelons la même méthode depuis le corps de la méthode interne.
Syntaxe :
returntype methodName()
{
//logic for application
methodName();//recursive call
}
Exemple :
La factorielle d'un nombre est un exemple de récursion directe. Le principe de base de la récursivité est de résoudre un problème complexe en le divisant en problèmes plus petits. Par exemple, dans le cas de la factorielle d'un nombre, on calcule la factorielle de « i » si l'on connaît sa factorielle de « i-1 ».
Code :
public class Factorial {
static int fact(int i){
if (i == 1)
return 1;
else
return(i * fact(i-1));
}
public static void main(String[] args) {
System.out.println("The factorial of given number 6 is: "+fact(6));
}
}
Sortie :

2. Appel récursif indirect/mutuel
Si on appelle une méthode depuis une autre méthode et une autre méthode appelée depuis la première méthode, vice versa.
Syntaxe :
<firstIndirectRecursive()
{
// Logic
secondIndirectRecursive();
}
secondIndirectRecursive()
{
//Logic
firstIndirectRecursive();
}
Exemple :
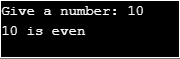
Pour montrer la récursion indirecte, nous prenons le programme suivant utilisé pour savoir si un nombre donné est pair ou impair à partir de l'entrée donnée.
Code :
import java.util.Scanner;
public class IndirectRecursion {
public static boolean oddNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return false;
} else {
return evenNum(i-1);
}
}
public static boolean evenNum(int i) {
if (i<0) throw new IllegalArgumentException("Number is negative");
if(i == 0){
return true;
} else {
return oddNum(i-1);
}
}
public static void main(String[] args) {
Scanner inputNum = new Scanner(System.in);
System.out.print("Give a number: ");
int n = inputNum.nextInt();
if (evenNum(n)) System.out.println(n + " is even");
else System.out.println(n + " is odd");
inputNum.close();
}
}
Sortie :
Exemples de récursion en Java
Voici quelques exemples supplémentaires pour résoudre les problèmes en utilisant la méthode de récursion.
Exemple n°1 – Séquence de Fibonacci
Un ensemble de « n » nombres est dit dans une séquence de Fibonacci si numéro3=numéro1+numéro2, c'est-à-dire que chaque nombre est une somme de ses deux nombres précédents. Par conséquent, la séquence commence toujours par les deux premiers chiffres comme 0 et 1. Le troisième chiffre est une somme de 0 et 1 résultant en 1, le quatrième nombre est l'addition de 1 et 1 résultant en 2, et la séquence continue.
Découvrez le code suivant en Java pour générer une séquence de Fibonacci :
Code :
public class FibonacciSeries{
static int num1=0,num2=1,num3=0;
static void fibonacci(int n){
if(n>0){
num3 = num1 + num2;
num1 = num2;
num2 = num3;
System.out.print(" "+num3);
fibonacci(n-1);
}
}
public static void main(String args[]){
int n=10;
System.out.print(num1+" "+num2);//printing constant first two digits 0 and 1
fibonacci(n-2);//Since first two numbers are already done
}
}
Sortie :

Ici, les deux premiers nombres sont initialisés à 0 et 1 et imprimés. Les variables « num1 », « num2 » et « num3 » sont utilisées pour générer la séquence requise. La variable « num3 » est obtenue en ajoutant « num1 » et « num2 », et les nombres sont décalés d'une position vers la gauche en les mélangeant comme indiqué dans le code. La fonction « Fibonacci » est ici appelée de manière récursive, et à chaque itération, la valeur de « n » est diminuée de 1. Ainsi la récursion se termine dès que « n » atteint la valeur 0.
Exemple n°2 – Tour de Hanoï
Il s'agit d'un problème mathématique classique qui consiste à avoir 3 pôles et un nombre « n » de disques de tailles différentes. Le puzzle est le suivant :
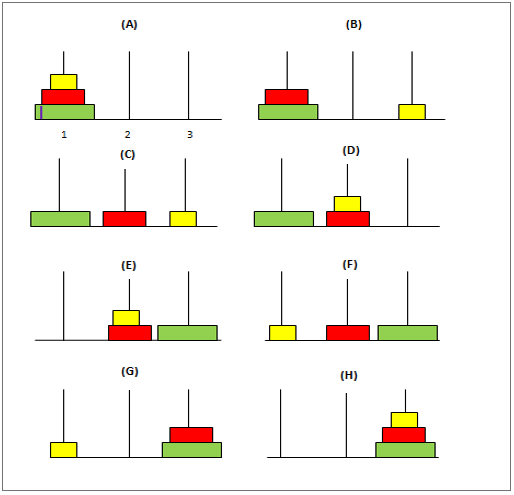
Au début, le premier pôle aura les disques disposés de telle sorte que le plus grand disque de tous soit en bas et le plus petit en haut du pôle. L'objectif est de déplacer ces disques du premier pôle au troisième pôle en gardant les disques dans la même position que celui du premier. Voici quelques conditions à garder à l'esprit lors du déplacement de ces disques :
- À la fois, un seul disque doit être déplacé.
- Dans le processus, il n'est pas permis de placer un disque plus grand sur un plus petit.
- Le deuxième pôle (du milieu) peut être utilisé comme médiateur lors du transfert des disques du premier au deuxième pôle.
Voici le code Java qui peut être utilisé pour résoudre le puzzle :
Code :
public class TowerOfHanoi {
public static void main(String[] args) {
int count = 3;
tower(count, 'A', 'B', 'C');
}
public static void tower(int first, char disk1, char temp, char disk2) {
if (first == 1) {
System.out.println("Disk 1 from " + disk1 + " to " + disk2);
} else {
tower(first - 1, disk1, disk2, temp);
System.out.println("Disk " + first + " from " + disk1 + " to " + disk2);
tower(first - 1, temp, disk1, disk2);
}
}
}
Sortie :
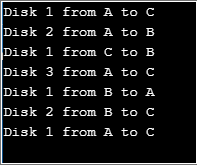
Here the variable “count” represents the number of discs to be used. The function “tower” is the recursive function used to move the discs from rod 1 to rod 3. A simple solution to this problem can be provided by considering 2 discs at first.
- First, we start by moving disc1 from rod 1 to rod 2.
- Next, we move disc2 to rod 3.
- Finally, we finish by moving disc1 to rod 3, completing the required solution.
This same principle is applied for the “n” number of discs by moving (n-1)the disc from rod 1 to 2 and following similar steps as above.
Example #3 – Factorial of Number
Code:
package com.recursion;
import java.util.Scanner;
public class FactorialOfNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Which number factorial do you want?=>");
//taking input from the user
int input = scanner.nextInt();
System.out.println("Factorial of " + input + "! is=>"+getMyFactorialNumber(input));
scanner.close();
}
public static long getMyFactorialNumber(int inputNumber) {
if (inputNumber == 1)//base condition
return 1;
return inputNumber * getMyFactorialNumber(inputNumber - 1);//recursive call
}
}
Output:
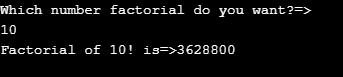
Example #4 – Armstrong Number
Code:
import java.util.Scanner;
//ARMSTRONG number means sum of numbers of cubes equal to the number
public class ArmstrongNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number?=>");
// taking input from the user
int input = scanner.nextInt();
//calling isArmstrongNumber() method and put in a variable
double checkNumber=isArmstrongNumber(input);
//checking the number
if(input==checkNumber)
{
System.out.println(input+" is ARMSTRONG NUMBER");
}
else
{
System.out.println(input+" not is ARMSTRONG NUMBER");
}
scanner.close();
}
static int remainderNumber;
static double total = 0;
public static double isArmstrongNumber(int inputNumber) {
if (inputNumber > 0) {
remainderNumber = inputNumber % 10;//separating digits
total = total + Math.pow(remainderNumber, 3);//cubes sum
isArmstrongNumber(inputNumber / 10);//recursive call
}
return total;
}
}
Output:
Example #5 – Palindrome Number
Code:
import java.util.Scanner;
public class PalindromeNumber {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Enter any Number=>");
// taking input from the user
int input = scanner.nextInt();
int checkNumber = palindromeNumberOrNot(input,0);
if (checkNumber == input)
{
System.out.println(input+" is a PALINDROME NUMBER");
}
else
{
System.out.println(input+" is not a PALINDROME NUMBER");
}
scanner.close();
}
public static int palindromeNumberOrNot(int inputNumber,int baseNumber) {
if (inputNumber == 0)// base case
return baseNumber;
baseNumber = (baseNumber * 10) + (inputNumber % 10);// getting the reverse of the number and stores in temp
return palindromeNumberOrNot(inputNumber/10,baseNumber);//recursive call
}
}
Output:
Conclusion
Recursive functions are relatively simpler to code, but they are also not that efficient as compared to the other existing methods. Hence they are majorly used in cases where the time given for development is less and also where a significant pattern can be observed in the problem.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

