Algorithmes de tri en Java

Trier les informations dans un certain ordre, souvent dans un cadre de type tableau, revient à les organiser. Vous pouvez utiliser différentes exigences de séquence ; les plus populaires trient les nombres du plus petit au plus grand ou vice versa, ou trient lexicographiquement les chaînes. Nous couvrirons différents algorithmes, depuis des alternatives inefficaces mais intuitives jusqu'aux algorithmes efficaces implémentés efficacement en Java et dans d'autres langages si vous êtes intéressé par le fonctionnement du tri.

Différents algorithmes de tri en java

Il existe différents algorithmes de tri, et tous ne sont pas aussi efficaces. Afin de les comparer et de voir lesquels sont les plus performants, nous analyserons leurs complexités temporelles.

PUBLICITÉ Cours populaire dans cette catégorie MAÎTRISÉE JAVA - Spécialisation | 78 séries de cours | 15 tests simulés

1. Tri par insertion
2. Tri à bulles
3. Tri de sélection
4. Fusionner le tri
5. Tri en tas

1. Tri par insertion

Le concept derrière le tri par insertion divise la plage en sous-tableaux triés et non triés. La partie classée se trouve au début de la durée 1 et correspond au premier composant (côté gauche) du tableau. Nous nous déplaçons dans le tableau et élargissons la partie classifiée du tableau d'un composant à chaque itération. Lorsque nous développons, nous positionnons le nouvel élément dans le sous-tableau trié. Nous faisons cela en déplaçant tous les éléments vers la droite jusqu’à ce que nous constations que nous n’avons pas besoin de modifier le premier composant. Lorsque la partie en gras est triée par ordre croissant, par exemple dans le tableau suivant, cela apparaît :

1. 3 5 7 8 4 2 1 9 6 : Considérez 4 et insérez ceci est ce dont nous avons besoin. Nous changeons depuis 8 > 4
2. 2. 3 5 7 x 8 2 1 9 6
3. 3 5 x 7 8 2 1 9 6
4. 3 x 5 7 8 2 1 9 6
5. 3 4 5 7 8 2 1 9 6

Code :

public class InsertionSortEx {
public static void insertionSort(int[] arr) {
for (int x = 1; x < arr.length; x++) {
int current = arr[x];
int y = x - 1;
while(y >= 0 && current < arr[y]) {
arr[y+1] = arr[y];
y--;
}
arr[y+1] = current;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,7,8,4,2,1,9,6};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
insertionSort(arr1);//sorting array using insertion sort
System.out.println("After Insertion Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

Sortie :

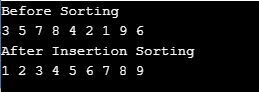
En suivant cette méthode, un composant a étendu la pièce triée ; nous avons maintenant cinq éléments au lieu de quatre. Chaque itération fait cela, et l'ensemble du tableau sera trié à la fin.

Remarque : C'est parce que nous devons transférer toute la liste classée une par une à chaque itération, ce qui est O(n). Nous devons faire cela pour chaque composant de chaque tableau, ce qui implique qu'il est borné par O(n^2).2.

2. Tri à bulles

Si la bulle n'est pas dans l'ordre requis, elle fonctionne en remplaçant les composants voisins. Ceci est répété jusqu'à ce que tous les composants soient en ordre dès le début du tableau. Nous savons que si nous parvenons à faire l'itération entière sans échanges, tous les éléments comparés à leurs éléments adjacents étaient dans l'ordre souhaitable et, par extension, le tableau entier. La raison de l'algorithme Bubble Sort est que les nombres ressemblent à des « bulles » dans le « sol ». Si, après un certain montant, vous parcourez à nouveau l'instance (4 est une bonne instance), vous remarquerez que le numéro se déplace lentement vers la droite.

Les étapes du tri des bulles sont les suivantes :

1. 4 21 5 3 : Ici, 1^st deux nombres ne sont pas dans le bon ordre ; nous devons donc trier les deux nombres.
2. 2 4 15 3 : Après cela, la paire de chiffres suivante n'est pas non plus dans le bon ordre. Le tri se reproduit donc.
3. 2 1 4 53 : Ces deux-là sont dans le bon ordre, 4 < 5, il n'est donc pas nécessaire de les échanger.
4. 2 1 4 5 3 : Encore une fois, nous devons échanger pour un ordre approprié.
5. 2 1 4 3 5 : Voici le tableau résultant après une itération.
6. Nous devons répéter ce processus jusqu'à ce que les chiffres soient dans le bon ordre.

Code :

public class BubbleSortExample {
public static void bubbleSort(int[] arr) {
int n = arr.length;
int tmp = 0;
for(int x=0; x < n; x++){
for(int y=1; y < (n-x); y++){
if(arr[y-1] > arr[y]){
//swap elements
tmp = arr[y-1];
arr[y-1] = arr[y];
arr[y] = tmp;
}
}
}
}
public static void main(String[] args) {
int arr[] ={4,2,1,5,3};
System.out.println("Array Before Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
System.out.println();
bubbleSort(arr);
System.out.println("Array After Bubble Sort");
for(int x=0; x < arr.length; x++){
System.out.print(arr[x] + " ");
}
}
}

Sortie :

Remarque : Cela aurait pu se terminer dans une boucle infinie si j'avais utilisé a[i]>= a[i+1 ] car cette connexion serait toujours valide avec des composants équivalents et les échangerait donc toujours d'un seul élément à un autre.

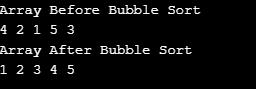
3. Tri de sélection

Selection Sort divise le tableau en un tableau de classifications qui ne sont pas triées. Cette fois, cependant, le sous-tableau de tri est formé en insérant à la fin du tableau trié l'élément minimum du sous-tableau non trié en échangeant :

1. 3 5 12 4
2. 15 3 2 4
3. 1 23 5 4
4. 1 2 35 4
5. 1 2 3 45
6. 1 2 3 4 5

Code :

public class SelectionSortEx {
public static void selectionSort(int[] arr){
for (int x = 0; x < arr.length - 1; x++)
{
int indx = x;
for (int y = x + 1; y < arr.length; y++){
if (arr[y] < arr[indx]){
indx = y;
}
}
int smallNumber = arr[indx];
arr[indx] = arr[x];
arr[x] = smallNumber;
}
}
public static void main(String a[]){
int[] arr1 = {3,5,1,2,4};
System.out.println("Before Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
System.out.println();
selectionSort(arr1);
System.out.println("After Selection Sorting");
for(int x:arr1){
System.out.print(x+" ");
}
}
}

Sortie :

Note: The minimum is O(n) for the array size because all the components must be checked. For each element of the array, we must find the minimum and make the whole process O (n^2) limited.

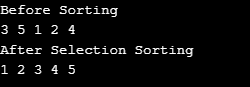
4. Merge Sort

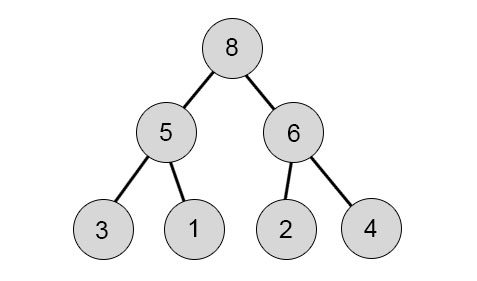
Merge Sort utilizes recursion to fix the issue of the divide and conquest method more effectively than earlier described algorithms.

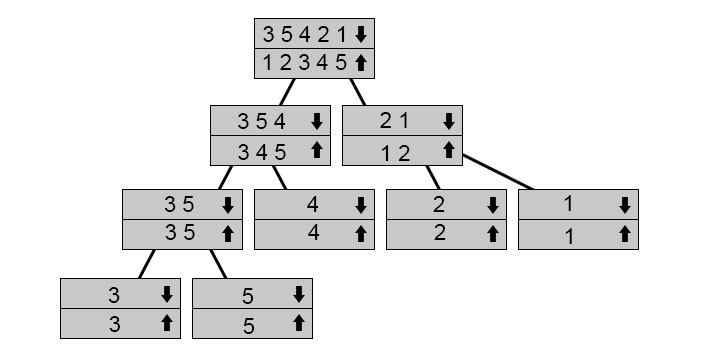
This tree shows how the recursive calls function. Down arrow marked arrays are the arrays for which we call function while we fuse up arrow arrays. Then you follow the arrow to the tree’s edge and then return and merge. We’ve got 3 5 3 1 range, so we split it into 3 5 4 and 2 1. We split them into their parts in order to sort them. We begin fusioning and sorting them as we go when we get to the bottom.

Code:

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class MergeSort {
static void merge(int[] array,int lowval,int midval,int highval){
int x, y ,k;
int[] c= new int[highval-lowval+1];
k = 0;
x=lowval;
y=midval+1;
while(x<=midval && y<=highval){
if(array[x]<=array[y]){
c[k++] = array[x++];
}
else{
c[k++] = array[y++];
}
}
while(x<=midval){
c[k++] = array[x++];
}
while(y<=highval){
c[k++] = array[y++];
}
k=0;
for(x = lowval; x<=highval; x++){
array[x] = c[k++];
}
}
static void mergeSort(int[] array,int lowval, int highval){
if(highval-lowval+1>1){
int midval = (lowval+highval)/2;
mergeSort(array,lowval,midval);
mergeSort(array,midval+1,highval);
merge(array,lowval,midval,highval);
}
}
public static void main(String[] args) {
BufferedReader r = new BufferedReader(new InputStreamReader(System.in));
int size;
System.out.println("Enter the array");
try {
size = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("Please Enter valid Input");
return;
}
int[] array = new int[size];
System.out.println("Enter array elements");
int x;
for (x = 0; x < array.length; x++) {
try {
array[x] = Integer.parseInt(r.readLine());
} catch (Exception e) {
System.out.println("An error Occurred");
}
}
System.out.println("After Sorting");
System.out.println(Arrays.toString(array));
mergeSort(array,0,array.length-1);
System.out.println("Before Merge Sorting");
System.out.println(Arrays.toString(array));
}
}

In this program, we have asked the user to enter input. The output will be in sorted order based on the user’s input.

Output:

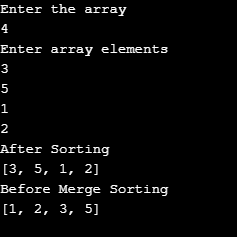
5. Heap Sort

You first must know the framework on which Heapsort operates-the heap-in order to comprehend why it operates. We will specifically speak about a binary heap, but you can also generalize this to other heap constructions. A heap is a tree that fulfills the property of the heap, namely that all its kids have relationships to each node. A heap must also be nearly finished. A near-complete d-depth binary has a d-1 subtree with the same root, and each node has a full, left subtree, with a left descending.

In other words, you get a lower and lower number (min-heap) or larger and bigger (max-heap) when moving down the tree. Here is a max-heap instance:

1. 6 1 8 3 5 2 4: Here, Both children’s numbers are smaller than the parent; hence we do not have to change anything.
2. 6 1 8 3 52 4: Here, 5 > 1, we need to swap them. We need to heapify for 5.
3. 6 5 8 3 12 4: Both of the children’s numbers are smaller; everything remains the same.
4. 6 5 83 1 2 4: Here, 8 > 6, hence we should swap them.
5. 8 5 6 3 1 2 4: After this iteration, we will get this result.

After Repeating this process again, we will get the following results:

• 8 5 6 3 1 2 4
1. 4 5 6 3 1 2 8: Swapping
2. 6 5 4 3 1 2 8: Heapify
3. 2 5 4 3 1 6 8: Swapping
4. 5 2 4 2 1 6 8: Heapify
5. 1 2 4 2 5 6 8: Swapping

Code:

public class HeapSort
{
public void sort(int arr[])
{
int n = arr.length;
for (int x = n / 2 - 1; x >= 0; x--)
heapify(arr, n, x);
for (int x=n-1; x>=0; x--)
int tmp = arr[0];
arr[0] = arr[x];
arr[x] = tmp;
heapify(arr, x, 0);
}
}
void heapify(int arr[], int n, int x)
{
int largest = x;
int L = 2*x + 1;
int r = 2*x + 2;
if (L < n && arr[L] > arr[largest])
largest = L;
if (r < n && arr[r] > arr[largest])
largest = r;
if (largest != x)
{
int swap = arr[x];
arr[x] = arr[largest];
arr[largest] = swap;
heapify(arr, n, largest);
}
}
static void printArray(int arr[])
{
int n = arr.length;
for (int x=0; x<n; ++x)
System.out.print(arr[x]+" ");
System.out.println();
}
public static void main(String args[])
{
int arr[] = {6,1,8,3,5,2,4};
int n = arr.length;
System.out.println("Before Sorting:");
printArray(arr);
HeapSort ob = new HeapSort();
ob.sort(arr);
System.out.println("After Heap Sorting:");
printArray(arr);
}
}

Output:



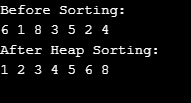
You can view it from point to level of the graph, from left to right. We achieved here that when we have the kth component in the array, the position of its children is 2\*k+1 and 2\*k+2 (assuming that indexing begins at 0). You can monitor this. The position of the parent is always (k-1)/2 for the kth component. You can readily “max heap up” any range because you know that. Check whether one of its kids is lower than that for each component. If so, pair one parent and repeat this step recursively with the parent.

Note: Since iterating for-loops across the entire array makes heapSort) (obviously O(N), it would create Heapsort O’s overall complexity(nlog n). Heapsort has an on-the-spot type, which means that it requires O(1) more room than Merge Sort, but it has some disadvantages, such as parallels that are hard.

Conclusion – Sorting Algorithms in Java

Sorting is a very prevalent procedure with datasets, whether for further analysis, speeding search with more effective algorithms relying on sorted information, filtering information, etc. Several languages endorse sorting, and often the interfaces obscure what the programmer does.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!