Maison >Périphériques technologiques >IA >Pourquoi ne le savais-je pas lorsque j'apprenais la génération de lignes : il existe une relation d'équivalence entre les matrices et les graphiques ?
Pourquoi ne le savais-je pas lorsque j'apprenais la génération de lignes : il existe une relation d'équivalence entre les matrices et les graphiques ?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBoriginal
- 2024-08-19 16:52:48720parcourir
La matrice est difficile à comprendre, mais elle peut être différente sous un autre angle.
Lors de l'apprentissage des mathématiques, nous sommes souvent frustrés par la difficulté et le caractère abstrait des connaissances que nous apprenons, mais parfois, simplement en changeant de perspective, nous pouvons trouver une solution simple et intuitive au problème ; Par exemple, lorsque nous apprenions la formule de la somme des carrés (a+b)² quand nous étions enfants, nous ne comprenons peut-être pas pourquoi elle est égale à a²+2ab+b². Nous savons seulement qu'elle est écrite ainsi dans le. livre et le professeur nous a demandé de nous en souvenir comme ceci ; jusqu'au jour où nous voyons cette image animée :
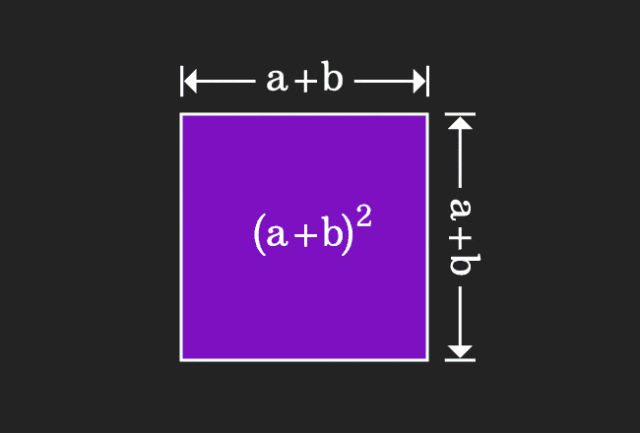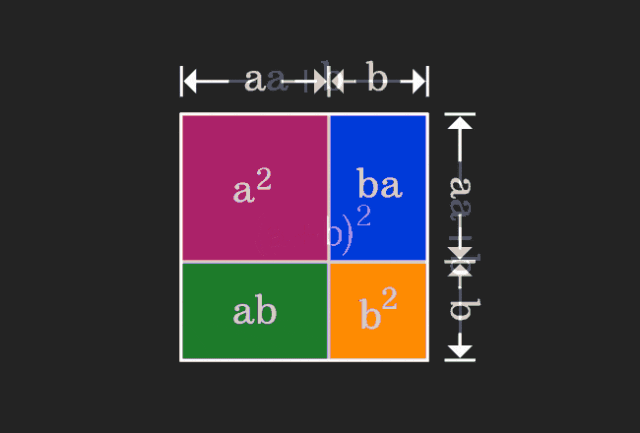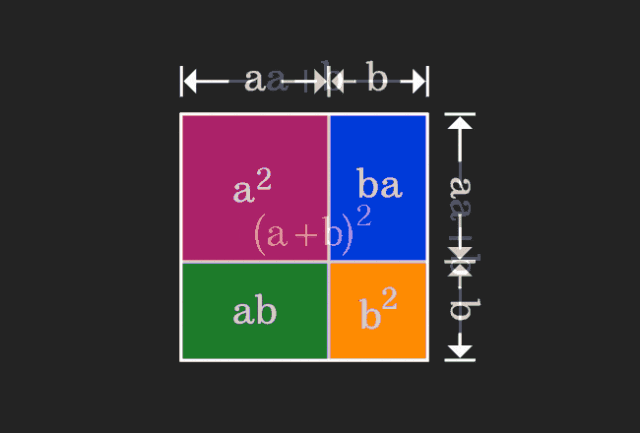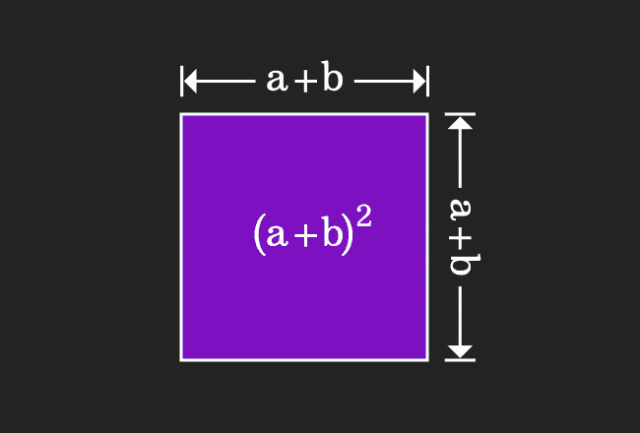
J'ai soudain réalisé qu'on pouvait la comprendre d'un point de vue géométrique !
Maintenant, ce sentiment d'illumination apparaît à nouveau : la matrice non négative peut être convertie de manière équivalente en le graphe orienté correspondant !
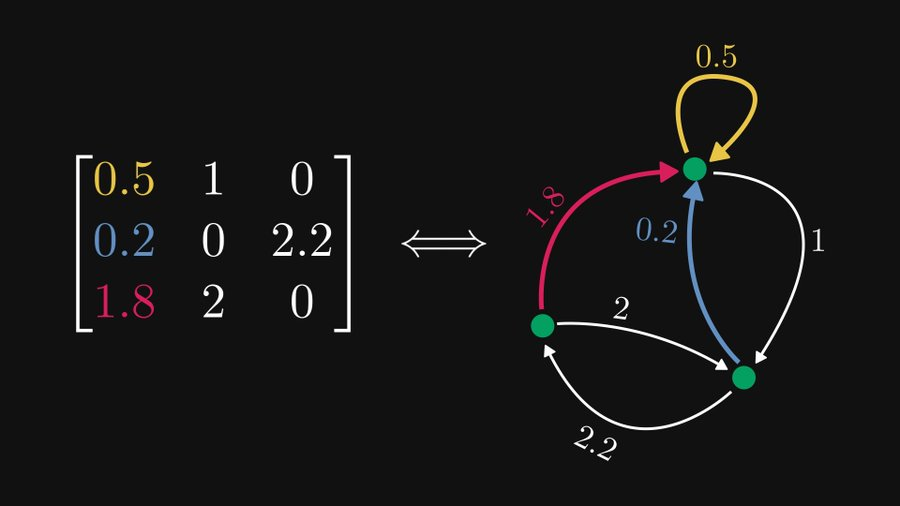
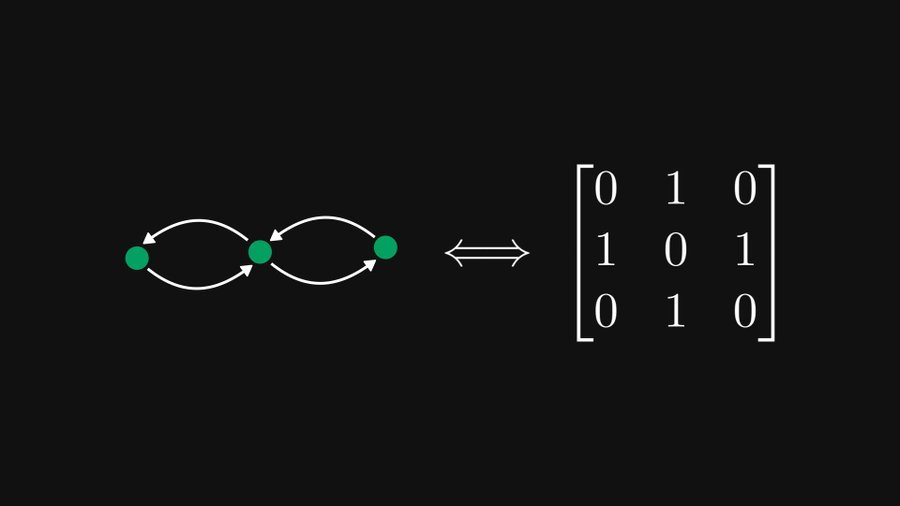
Comme le montre la figure ci-dessous, la matrice 3×3 à gauche peut en fait être représentée de manière équivalente comme un graphe orienté contenant trois nœuds à droite, et cette représentation est très utile pour la théorie des matrices et des graphes.
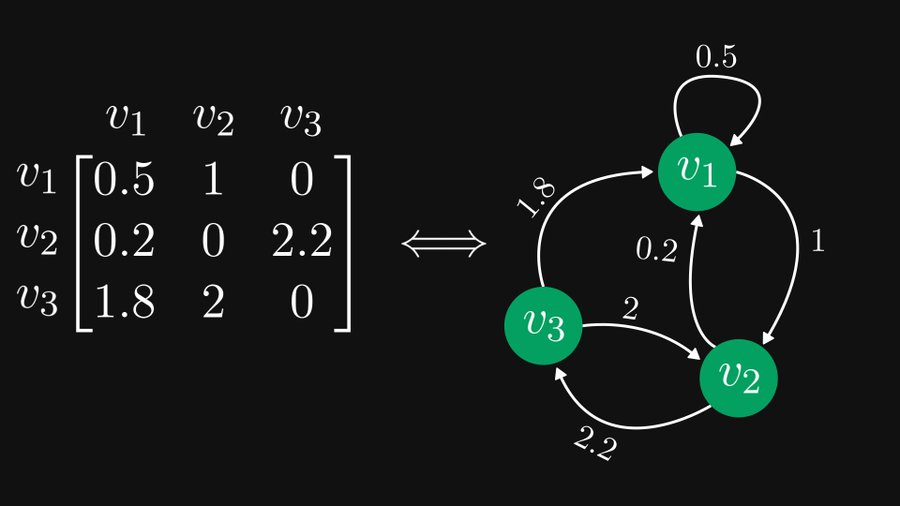
Cet exemple vient du mathématicien Tivadar Danka qui s'engage à rendre les mathématiques accessibles à tous. Le mathématicien autoproclamé « bon chaotique » a présenté de manière vivante cette équivalence des matrices et des graphiques ainsi que leurs utilisations dans une série de tweets et d’articles de blog. À ce jour, les tweets ont été lus plus de 2 millions de fois, ont recueilli plus de 3 200 retweets et 9 100 favoris.
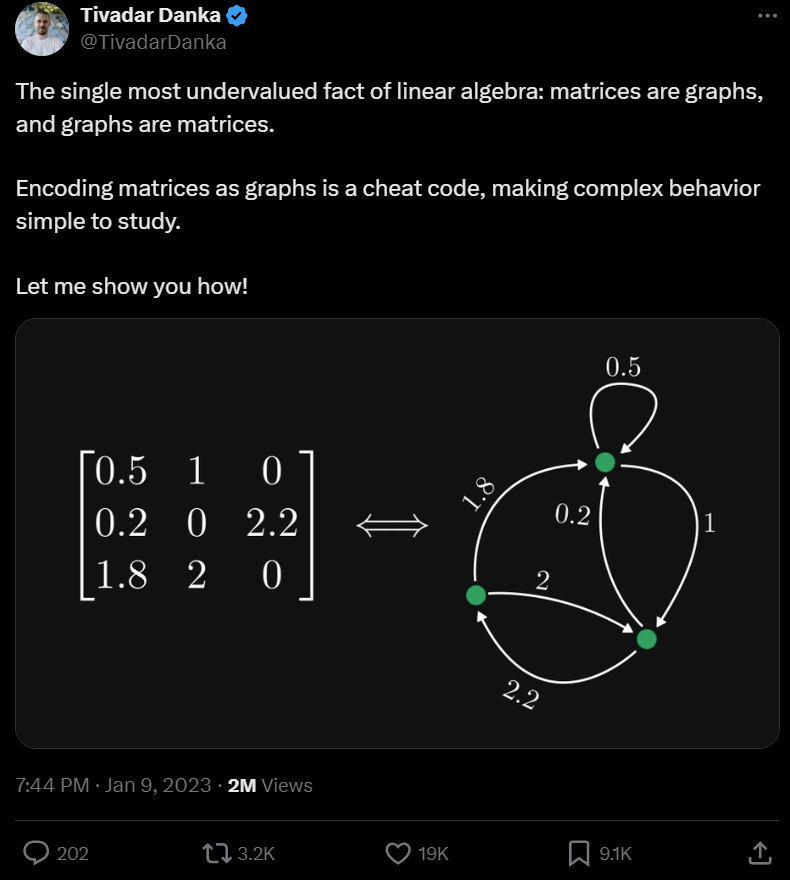
La valence des matrices et des graphiques orientés
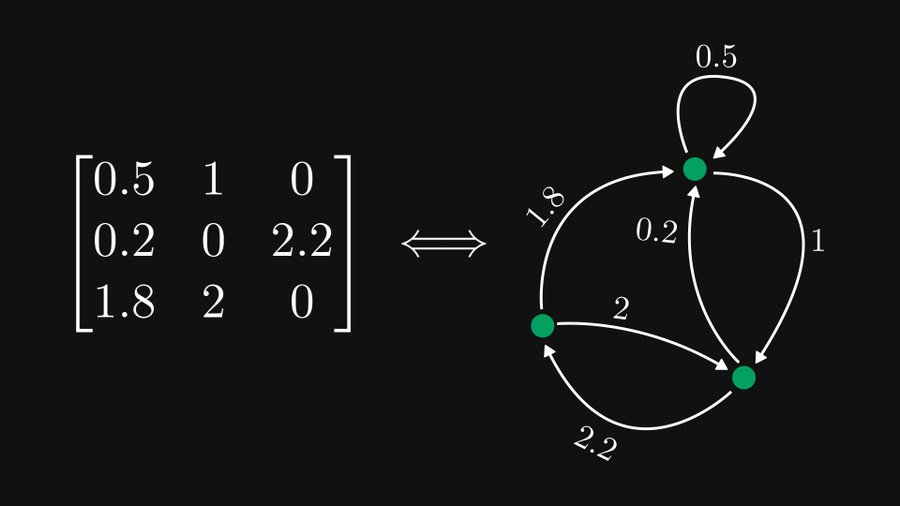
Comme le montre l'exemple ci-dessus, si nous traitons chaque ligne comme un nœud, alors chaque élément peut être représenté comme des arêtes orientées et pondérées. Bien entendu, 0 élément peut être ignoré. Si l'élément est situé à la ligne i et à la colonne j, il correspond au bord du nœud i au nœud j.
Cela peut paraître compliqué à première vue, mais nous pouvons d'abord examiner l'un des nœuds.
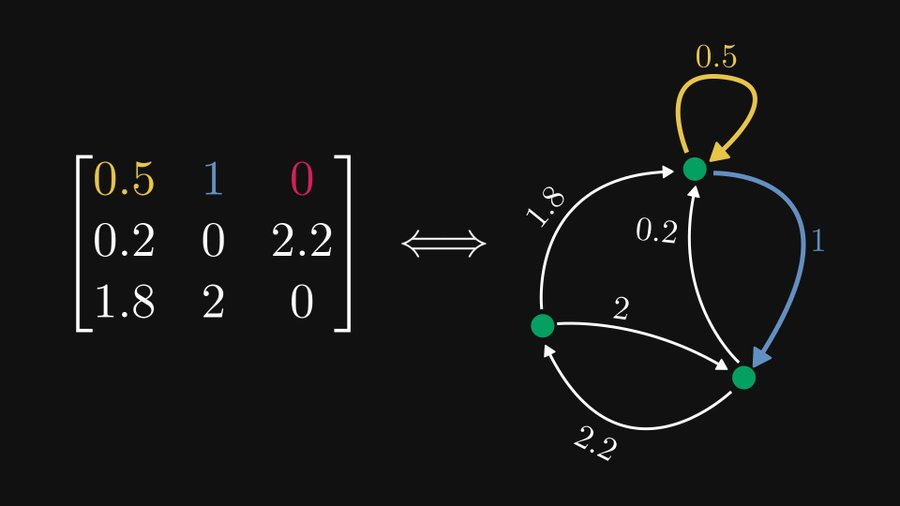
Comme le montre la figure, pour cette matrice 3×3, la ligne 1 correspond au nœud le plus haut (on l'appelle ici nœud 1), qui contient 3 éléments mais l'un d'eux est 0, donc ce nœud s'étend sur deux bords. Le bord jaune représente l'élément 0,5 en (1,1), c'est donc un bord dirigé pointant vers lui-même avec un poids de 0,5. De même, le bord bleu est le bord qui pointe vers le nœud 2 et a un poids de 1.
De cette façon, nous pouvons analyser que la i-ème colonne de la matrice correspond à toutes les arêtes pointant vers le i-ème nœud.
A quoi sert cette expression équivalente ?
Cette équivalence entre les matrices non négatives et les graphiques orientés peut non seulement nous aider à mieux comprendre les matrices et leurs opérations, mais aussi à simplifier certains processus de calcul, cela peut également nous aider à partir d'une nouvelle perspective de diagramme de compréhension ;
Par exemple, la puissance de la matrice correspond à la marche dans le graphique.
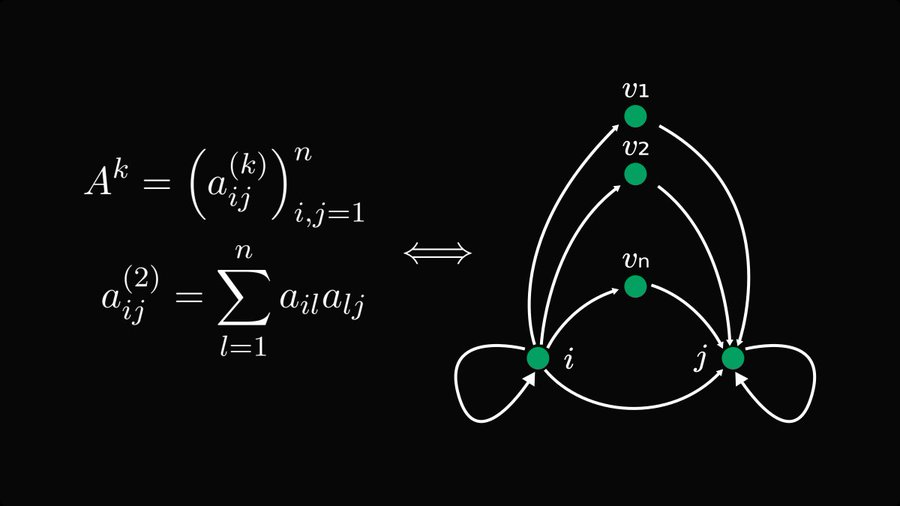
Comme le montre la figure ci-dessus, pour la k-ème puissance de la matrice carrée n×n A, le processus de sommation de chaque élément intégrera toutes les marches en k étapes possibles.
Par exemple, supposons que nous voulions calculer le carré de la matrice 3×3 ci-dessus.

Si nous utilisons la multiplication matricielle, nous devons la calculer comme ceci :
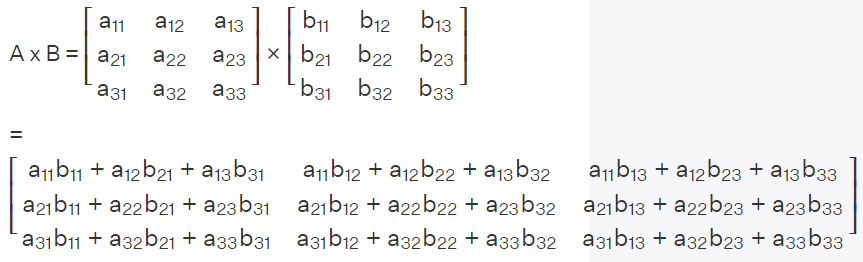
Pour le premier élément du résultat de l'opération, nous pouvons obtenir le résultat = 0,5×0,5+1×0,2+0×1,8 = 0,45. Enfin, nous pouvons obtenir le résultat complet sous la forme :

Mais si nous utilisons la méthode de marche graphique ci-dessus, nous pouvons obtenir le résultat en parcourant le chemin. De même, pour le premier élément de la matrice de résultats, nous devons résumer tous les chemins de marche en 2 étapes qui satisfont a_{1,l}→a_{l,1}.
Cependant, si ce graphe orienté représente l'état d'une chaîne de Markov, le carré de sa matrice de probabilité de transition représente essentiellement la probabilité que la chaîne atteigne un certain état après 2 étapes.
De plus, utiliser des graphiques pour représenter des matrices peut également nous donner une compréhension approfondie de la structure des matrices non négatives. Pour ce faire, Danka a déclaré que nous devons d'abord comprendre le concept de « composants fortement connectés ».
composant fortement connecté
Qu'est-ce qu'un composant fortement connecté ? Pour un graphe orienté, si tous les autres nœuds du graphe peuvent être atteints à partir de chaque nœud, nous disons que le graphe est fortement connecté. Comme indiqué ci-dessous.
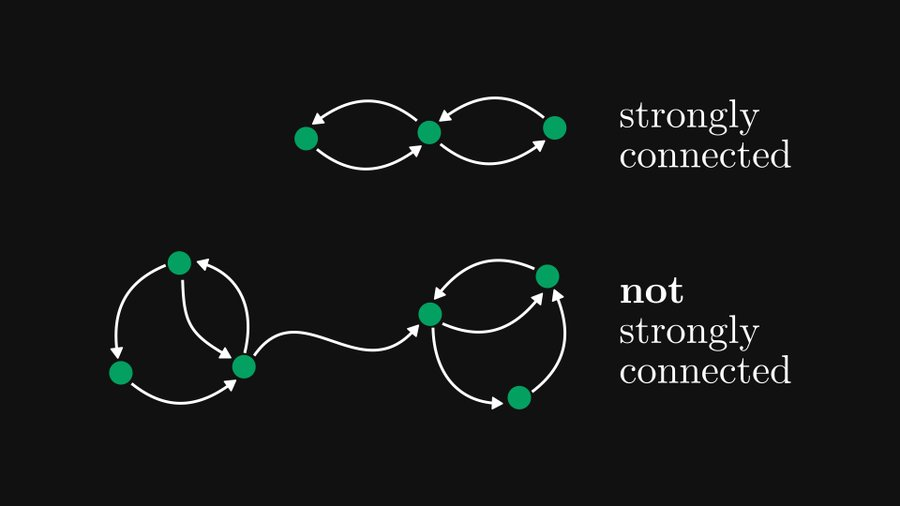
Le composant fortement connecté fait référence à la partie/sous-graphe dans le graphe orienté qui peut atteindre une forte connectivité. Comme le montre la figure ci-dessous, il y a un composant fortement connecté à gauche et à droite, tandis que le bord blanc au milieu n'appartient à aucun composant fortement connecté.
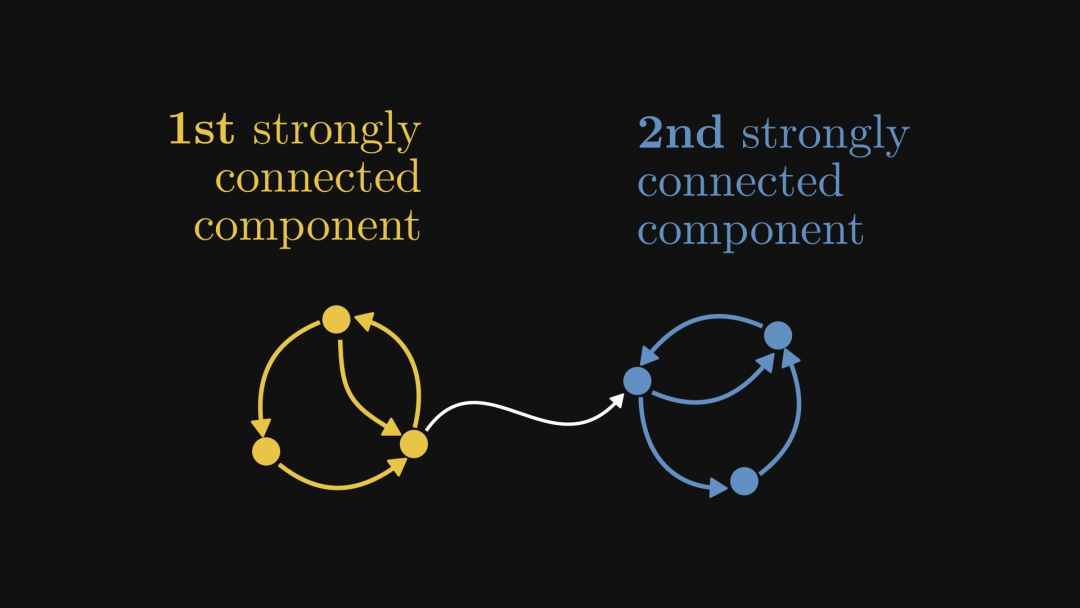
L'image ci-dessous montre un autre exemple, où la partie jaune est le composant fortement connecté :
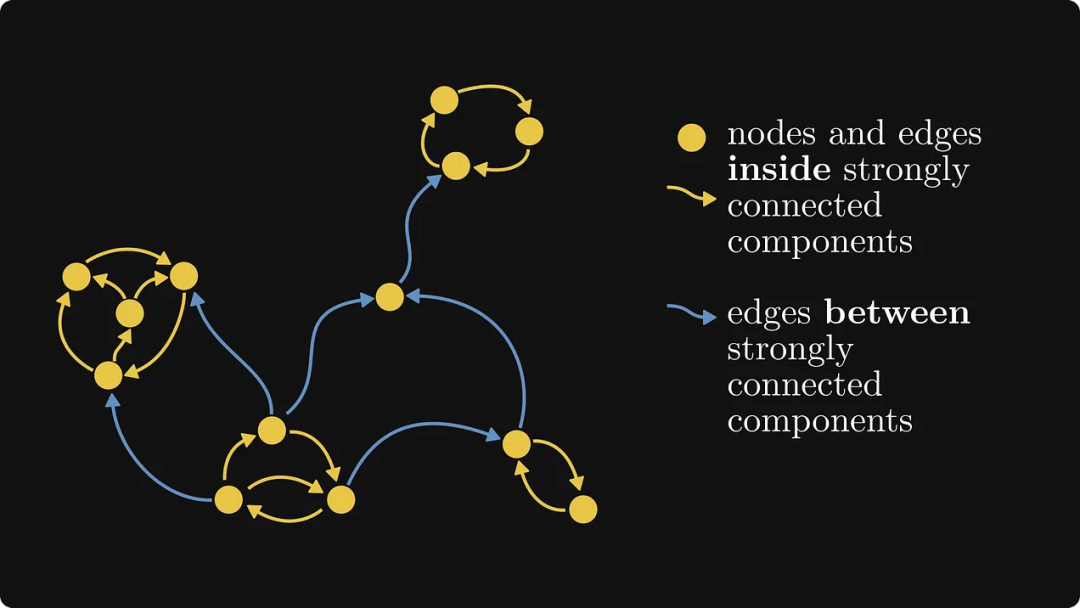 # 🎜🎜#
# 🎜🎜#
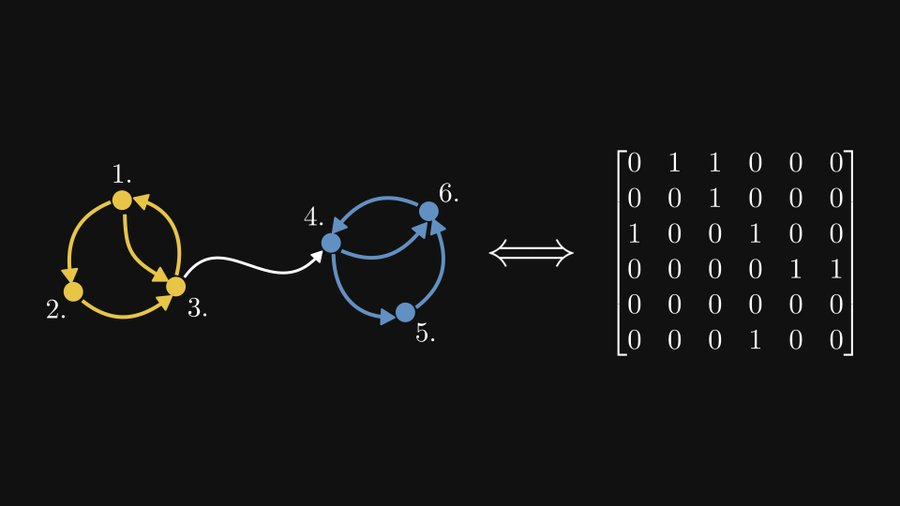
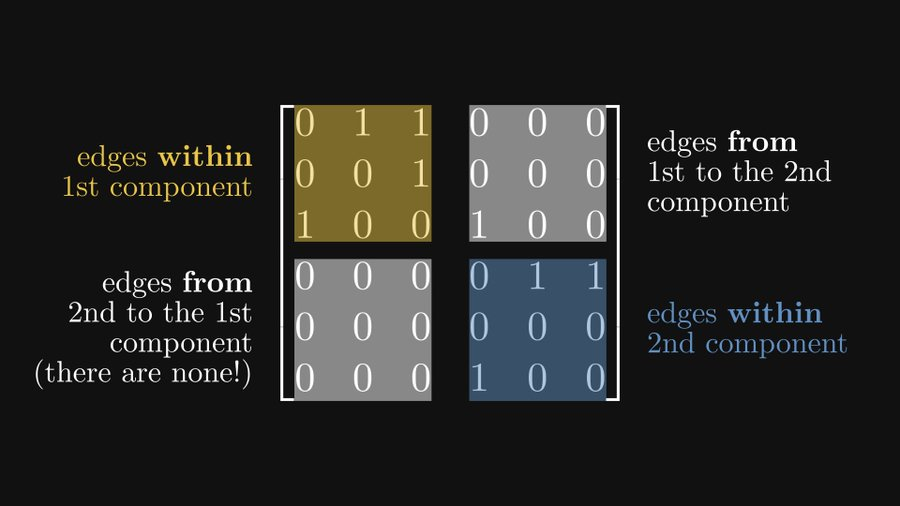

- Construire le graphe orienté correspondant pour la matrice non négative
- ; Trouvez-le Le composant fortement connecté ;
- Changez pour une meilleure façon d'étiqueter chaque nœud.
Utilisez des images pour obtenir le formulaire standard Frobenius
Alors, quelle est cette meilleure façon ? Sur la base de l'exemple ci-dessus, jetons un coup d'œil au processus. Tout d'abord, chaque composant fortement connecté est fusionné en un seul objet, comme le montre la figure ci-dessous. À l’heure actuelle, nous pouvons traiter chaque composant fortement connecté comme une boîte noire : nous ne nous soucions pas de sa structure interne, seulement de ses connexions externes.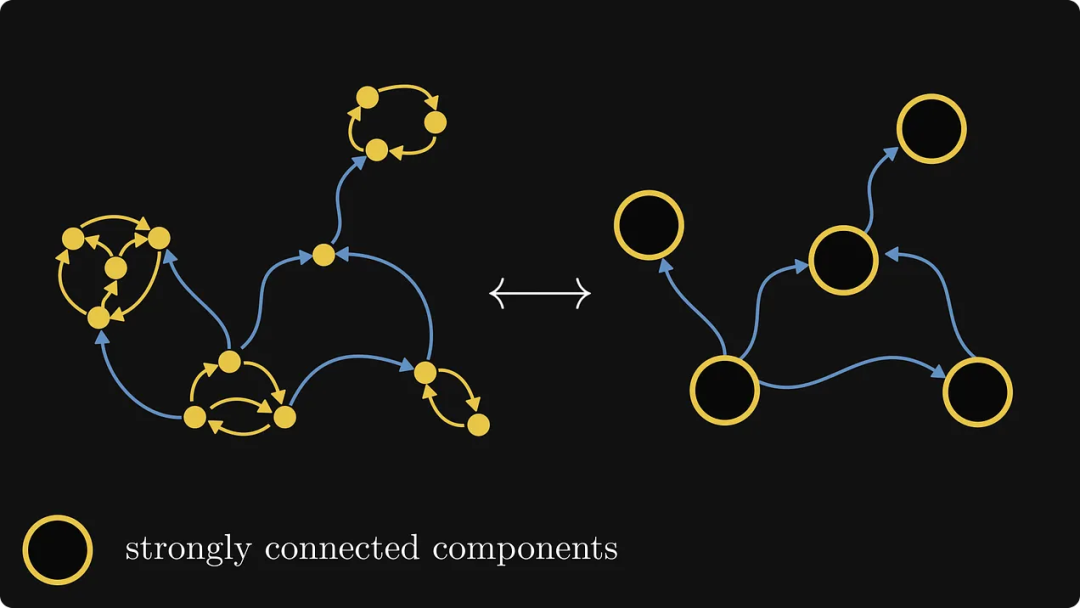
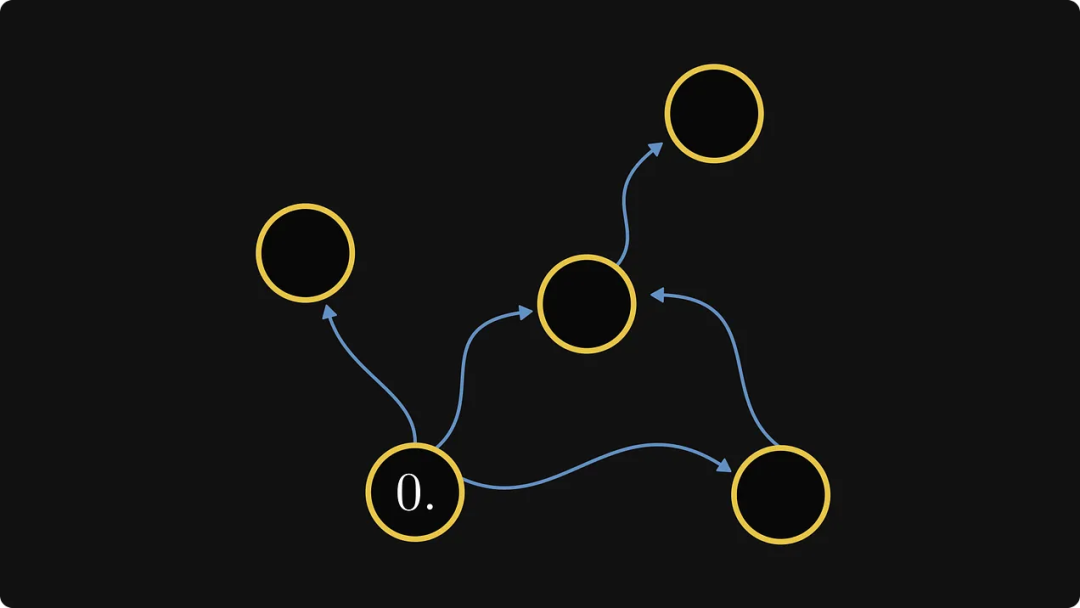
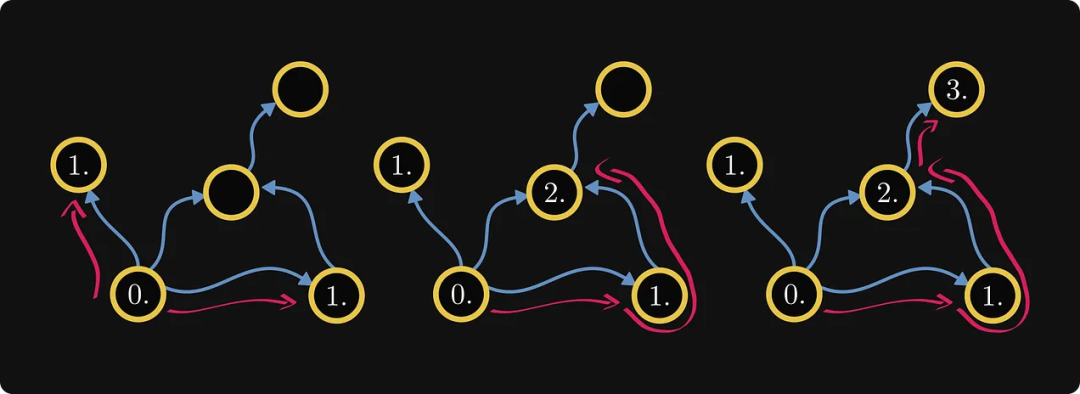
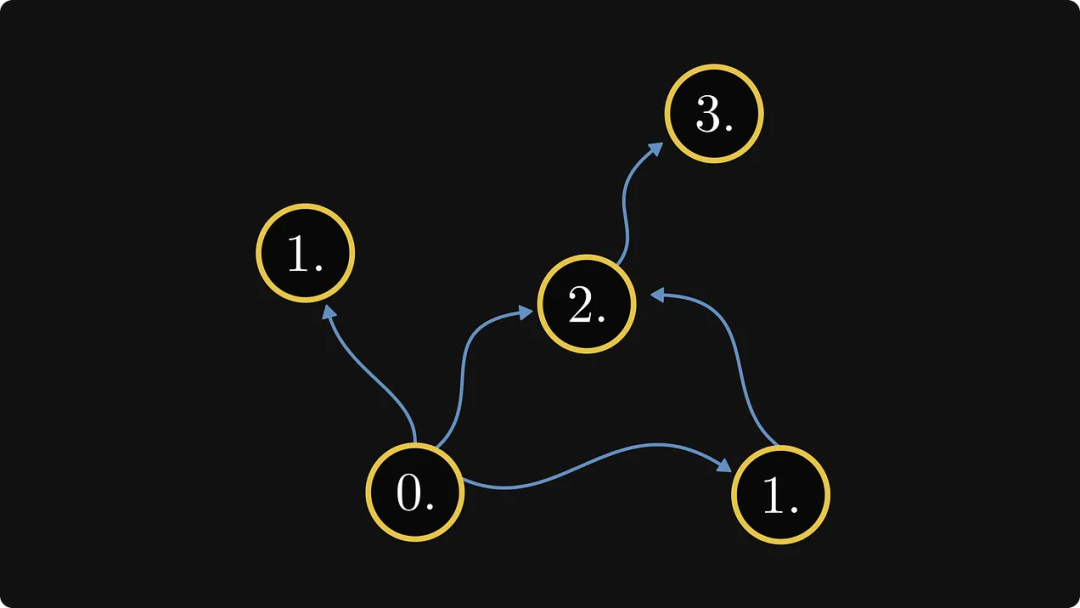
En fait, cela définit l'ordre des composants. Ensuite, étiquetez les nœuds internes de chaque composant :
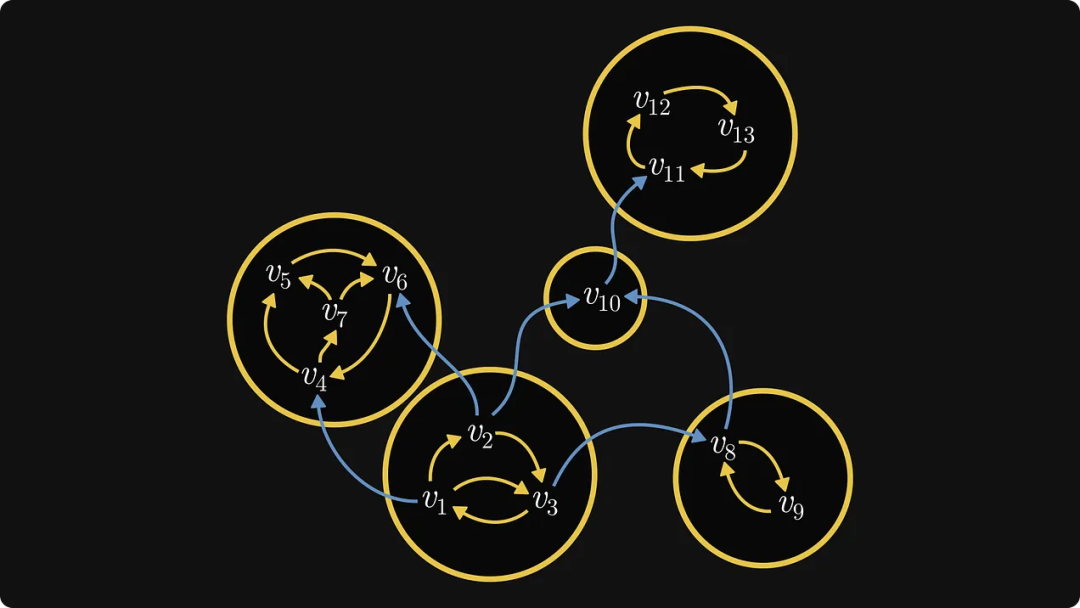
Si le graphe lui-même provient d'une matrice, alors un tel processus de réétiquetage peut aboutir à une matrice canonique de Frobenius !

En fait, ce processus de réétiquetage consiste à utiliser une matrice de permutation P pour transformer la matrice d'origine, et la matrice de permutation est composée du produit de plusieurs matrices transposées.
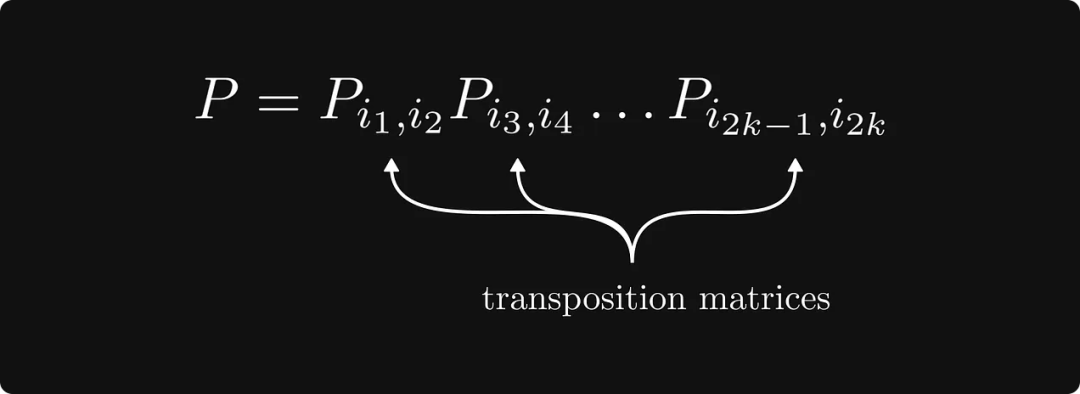
Ce qui suit est la forme complète du théorème :

Bien sûr, l'utilisation de graphiques pour représenter des matrices va bien au-delà. Par exemple, nous pouvons également utiliser les valeurs propres de la matrice. pour définir les valeurs propres du graphe. En fait, cette ligne de pensée a donné naissance au domaine de recherche de la théorie des graphes spectraux.
Conclusion
Évidemment, cette relation d'équivalence entre matrices et graphiques est non seulement utile pour la recherche en théorie des graphes, mais offre également une nouvelle perspective pour le calcul et l'analyse de l'algèbre linéaire. Il a également des utilisations pratiques importantes. Par exemple, les données ADN sont souvent représentées sous forme de matrices ou de graphiques.
De plus, nous connaissons tous l'importance des opérations matricielles pour l'IA actuelle à grand modèle, et les graphiques représentés par des graphes de connaissances deviennent également un moteur important de l'IA actuelle grâce à des technologies telles que la recherche améliorée par récupération. La connexion des deux pourrait apporter de nouvelles avancées en matière d’interprétabilité de l’IA et d’intelligence artificielle graphique. À tout le moins, cela nous aide à mieux apprendre l’algèbre linéaire.
En fait, le contenu ci-dessus est extrait du livre "Mathematics of Machine Learning" en cours d'écriture par Tivadar Danka. Ce livre présentera les connaissances mathématiques liées à l'apprentissage automatique, du niveau simple au niveau approfondi, permettant aux lecteurs de vraiment comprendre ce qui se passe et pourquoi. Danka déclare avec confiance qu'il s'agira de « la meilleure ressource pour l'apprentissage de l'apprentissage automatique ». À l'heure actuelle, il a publié deux aperçus de chapitres en ligne. Les lecteurs intéressés peuvent visiter : https://tivadardanka.com/mathematics-of-machine-learning-preview/
.Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI

