Recherche en largeur d'abord (BFS)

La recherche en largeur d'un graphique visite les sommets niveau par niveau. Le premier niveau est constitué du sommet de départ. Chaque niveau suivant est constitué des sommets adjacents aux sommets du niveau précédent. Le parcours en largeur d'un graphe est comme le parcours en largeur d'un arbre discuté dans Tree Traversal. Lors du parcours d'un arbre en largeur, les nœuds sont visités niveau par niveau. La racine est d’abord visitée, puis tous les enfants de la racine, puis les petits-enfants de la racine, et ainsi de suite. De même, la recherche en largeur d'un graphe visite d'abord un sommet, puis tous ses sommets adjacents, puis tous les sommets adjacents à ces sommets, et ainsi de suite. Pour garantir que chaque sommet n'est visité qu'une seule fois, il saute un sommet s'il a déjà été visité.

Algorithme de recherche en largeur

L'algorithme de recherche en largeur à partir du sommet v dans un graphe est décrit dans le code ci-dessous.

Entrée : G = (V, E) et un sommet de départ v
Sortie : un arbre BFS enraciné à v
1 Arbre bfs (sommet v) {
2 créer une file d'attente vide pour stocker les sommets à visiter ;
3 ajoutez v dans la file d'attente ;
4 points v visités ;
5
6 while (la file d'attente n'est pas vide) {
7 retirer un sommet, disons u, de la file d'attente ;
8 ajoutez-vous dans une liste de sommets traversés ;
9 pour chaque voisin w de toi
10 si w n'a pas été visité {
11 ajoutez w dans la file d'attente ;
12 vous définit comme parent de w dans l'arbre ;
13 points avec visite ;
14>
15>
16>

Considérez le graphique de la figure ci-dessous (a). Supposons que vous commenciez la recherche en largeur à partir du sommet 0. Visitez d’abord 0, puis visitez tous ses voisins, 1, 2 et 3, comme le montre la figure ci-dessous (b). Le sommet 1 a trois voisins : 0, 2 et 4. Puisque 0 et 2 ont déjà été visités, vous n'en visiterez désormais que 4, comme le montre la figure ci-dessous (c). Le sommet 2 a trois voisins, 0, 1 et 3, qui ont tous été visités. Le sommet 3 a trois voisins, 0, 2 et 4, qui ont tous été visités. Le sommet 4 a deux voisins, 1 et 3, qui ont tous été visités. Par conséquent, la recherche se termine.

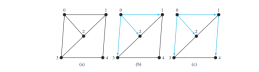
Comme chaque arête et chaque sommet n'est visité qu'une seule fois, la complexité temporelle de la méthode bfs est O(|E| + |V|), où | E| désigne le nombre d'arêtes et |V| le nombre de sommets.

Mise en œuvre de la recherche en largeur d'abord

La méthode bfs(int v) est définie dans l'interface Graph et implémentée dans la classe AbstractGraph.java (lignes 197 à 222). Il renvoie une instance de la classe Tree avec le sommet v comme racine. La méthode stocke les sommets recherchés dans la liste searchOrder (ligne 198), le parent de chaque sommet du tableau parent (ligne 199), utilise une liste chaînée pour une file d'attente (lignes 203-204), et utilise le tableau isVisited pour indiquer si un sommet a été visité (ligne 207). La recherche commence à partir du sommet v. v est ajouté à la file d'attente à la ligne 206 et est marqué comme visité (ligne 207). La méthode examine maintenant chaque sommet u dans la file d'attente (ligne 210) et l'ajoute à searchOrder (ligne 211). La méthode ajoute chaque voisin non visité e.v de u à la file d'attente (ligne 214), définit son parent sur u (ligne 215) et le marque comme visité (ligne 216).

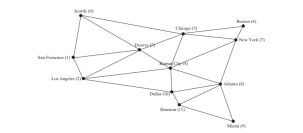
Le code ci-dessous donne un programme de test qui affiche un BFS pour le graphique de la figure ci-dessus à partir de Chicago.

public class TestBFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph<string> graph = new UnweightedGraph(vertices, edges);
        AbstractGraph<string>.Tree bfs = graph.bfs(graph.getIndex("Chicago"));

        java.util.List<integer> searchOrders = bfs.getSearchOrder();
        System.out.println(bfs.getNumberOfVerticesFound() + " vertices are searched in this BFS order:");
        for(int i = 0; i 



<p>12 sommets sont recherchés dans cet ordre :<br>
 Chicago Seattle Denver Kansas City Boston New York<br>
 San Francisco Los Angeles Atlanta Dallas Miami Houston<br>
Le parent de Seattle est Chicago<br>
Le parent de San Francisco est Seattle<br>
Le parent de Los Angeles est Denver<br>
Le parent de Denver est Chicago<br>
Le parent de Kansas City est Chicago<br>
le parent de Boston est Chicago<br>
Le parent de New York est Chicago<br>
Le parent d'Atlanta est Kansas City<br>
Le parent de Miami est Atlanta<br>
Le parent de Dallas est Kansas City<br>
Le parent de Houston est Atlanta</p>

<h2>
  
  
  Applications du BFS
</h2>

<p>De nombreux problèmes résolus par le DFS peuvent également être résolus à l'aide du BFS. Plus précisément, le BFS peut être utilisé pour résoudre les problèmes suivants :</p>
<ul>
<li>Détecter si un graphique est connecté. Un graphe est connecté s'il existe un chemin entre deux sommets quelconques du graphe.</li>
<li>Détecter s'il existe un chemin entre deux sommets.</li>
<li>Trouver le chemin le plus court entre deux sommets. Vous pouvez prouver que le chemin entre la racine et n'importe quel nœud de l'arborescence BFS est le chemin le plus court entre la racine et le nœud.</li>
<li>Trouver tous les composants connectés. Un composant connexe est un sous-graphe connexe maximal dans lequel chaque paire de sommets est reliée par un chemin.</li>
<li>Détecter s'il y a un cycle dans le graphique.</li>
<li>Trouver un cycle dans le graphique.</li>
<li>Tester si un graphe est biparti. (Un graphe est biparti si les sommets du graphe peuvent être divisés en deux ensembles disjoints de telle sorte qu'aucune arête n'existe entre les sommets du même ensemble.)</li>
</ul>

<p><img src="/static/imghwm/default1.png" data-src="https://img.php.cn/upload/article/000/000/000/172324339470608.png?x-oss-process=image/resize,p_40" class="lazy" alt="Breadth-First Search (BFS)"></p>


          

            
        </integer></string></string>

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!