Maison >Périphériques technologiques >IA >Formation avec des millions de données cristallines pour résoudre le problème de la phase cristallographique, la méthode d'apprentissage profond PhAI est publiée dans Science
Formation avec des millions de données cristallines pour résoudre le problème de la phase cristallographique, la méthode d'apprentissage profond PhAI est publiée dans Science
- 王林original
- 2024-08-08 21:22:30851parcourir

À ce jour, les détails structurels et la précision déterminés par cristallographie, des métaux simples aux grandes protéines membranaires, sont inégalés par aucune autre méthode. Cependant, le plus grand défi, appelé problème de phase, reste la récupération des informations de phase à partir d'amplitudes déterminées expérimentalement.
Des chercheurs de l'Université de Copenhague, au Danemark, ont développé une méthode d'apprentissage en profondeur appelée PhAI pour résoudre les problèmes de phase cristalline. Un réseau neuronal d'apprentissage en profondeur formé à l'aide de millions de structures cristallines artificielles et de leurs données de diffraction synthétique correspondantes peut générer des cartes de densité électronique précises. .
La recherche montre que cette méthode de solution de structure ab initio basée sur l'apprentissage profond peut résoudre le problème de phase avec une résolution de seulement 2 angströms, ce qui équivaut à seulement 10 à 20 % des données disponibles à une résolution atomique, alors que l'ab initio traditionnel les méthodes nécessitent généralement une résolution atomique.
La recherche pertinente s'intitulait « PhAI : Une approche d'apprentissage en profondeur pour résoudre le problème de la phase cristallographique » et a été publiée dans « Science » le 1er août.
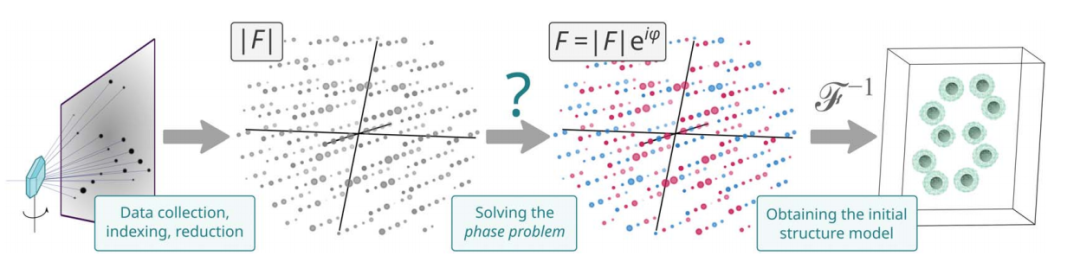
La cristallographie est l'une des principales techniques analytiques des sciences naturelles. La cristallographie aux rayons X offre une vue unique sur la structure tridimensionnelle des cristaux.
Afin de reconstruire la carte de densité électronique, il faut connaître suffisamment de facteurs de structure complexes $F$ des réflexions de diffraction. Dans une expérience traditionnelle, seule l'amplitude $|F|$ est obtenue, tandis que la phase $phi$ est perdue. Il s'agit d'un problème de phase cristallographique.
Une avancée majeure a eu lieu dans les années 1950 et 1960, lorsque Karle et Hauptmann** ont développé des méthodes dites directes pour résoudre les problèmes de phase. Mais la méthode directe nécessite des données de diffraction à résolution atomique. Cependant, l’exigence de résolution atomique est une observation empirique.
Ces dernières années, les méthodes directes traditionnelles ont été complétées par des méthodes à double espace. Les méthodes ab initio actuellement disponibles semblent avoir atteint leurs limites. Une solution générale au problème de phase reste inconnue.
Mathématiquement parlant, toute combinaison d'amplitude et de phase du facteur de structure peut être soumise à une transformée de Fourier inverse. Cependant, les exigences physiques et chimiques (comme avoir une distribution de densité électronique de type atomique) imposent des règles sur les combinaisons possibles de phases cohérentes avec un ensemble d'amplitudes. Les progrès de l’apprentissage profond permettent d’explorer cette relation, peut-être de manière plus approfondie que les méthodes ab initio actuelles.
Ici, des chercheurs de l'Université de Copenhague ont adopté une approche basée sur les données, utilisant des millions de structures cristallines artificielles et leurs données de diffraction correspondantes, dans le but de résoudre les problèmes de phase en cristallographie.
Une étude montre que cette méthode de solution de structure ab initio basée sur l'apprentissage profond peut être réalisée avec une résolution de seulement la distance minimale du plan de réseau (dmin) = 2,0 Å en utilisant uniquement les données requises par la méthode directe de 10 % à 20 % .
Conception et formation du réseau neuronal
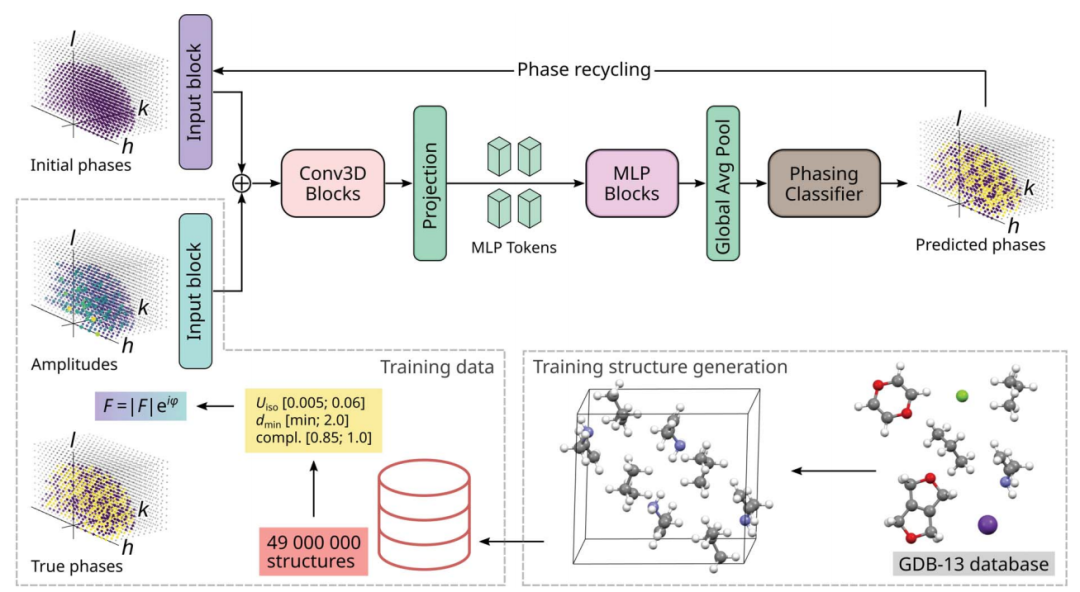
Le réseau neuronal artificiel construit est appelé PhAI, qui accepte l'amplitude du facteur de structure |F| et génère la valeur de phase correspondante ϕ. L'architecture de PhAI est présentée dans la figure ci-dessous.
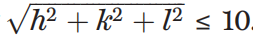
C'est-à-dire des structures limitées à des dimensions de cellule unitaire d'environ 10 Å à une résolution atomique. De plus, le groupe spatial centrosymétrique le plus courant, P21/c, a été choisi. La symétrie centrale limite les valeurs de phase possibles à zéro ou π rad.
- Recherche sur la formation de réseaux de neurones utilisant des structures cristallines artificielles contenant principalement des molécules organiques. Environ 49 000 000 de structures ont été créées, dont 94,29 % étaient des structures cristallines organiques, 5,66 % étaient des structures cristallines organométalliques et 0,05 % étaient des structures cristallines inorganiques.
- L'entrée du réseau neuronal se compose d'amplitude et de phase, qui sont traitées par un bloc d'entrée convolutif, ajoutées et introduites dans une série de blocs convolutifs (Conv3D), suivis d'une série de blocs de perceptron multicouche (MLP). La phase prédite du classificateur linéaire (classificateur de phase) parcourt le réseau Nc fois. Les données de formation ont été générées en insérant des atomes métalliques et des molécules organiques de la base de données GDB-13 dans des cellules unitaires. Les structures résultantes sont organisées en données d'entraînement à partir desquelles les véritables amplitudes de phase et de facteur de structure aux facteurs de température, à la résolution et à l'intégrité échantillonnés peuvent être calculées.
Résolvez de vrais problèmes structurels - Les réseaux de neurones entraînés fonctionnent sur des ordinateurs standard avec des exigences de calcul modérées. Il accepte en entrée une liste d’indices hkl et les amplitudes des facteurs de structure correspondants. Aucune autre information d'entrée n'est requise, pas même les paramètres de cellule unitaire de la structure. Ceci est fondamentalement différent de toutes les autres méthodes ab initio modernes. Le réseau peut prédire et générer des valeurs de phase à la volée.
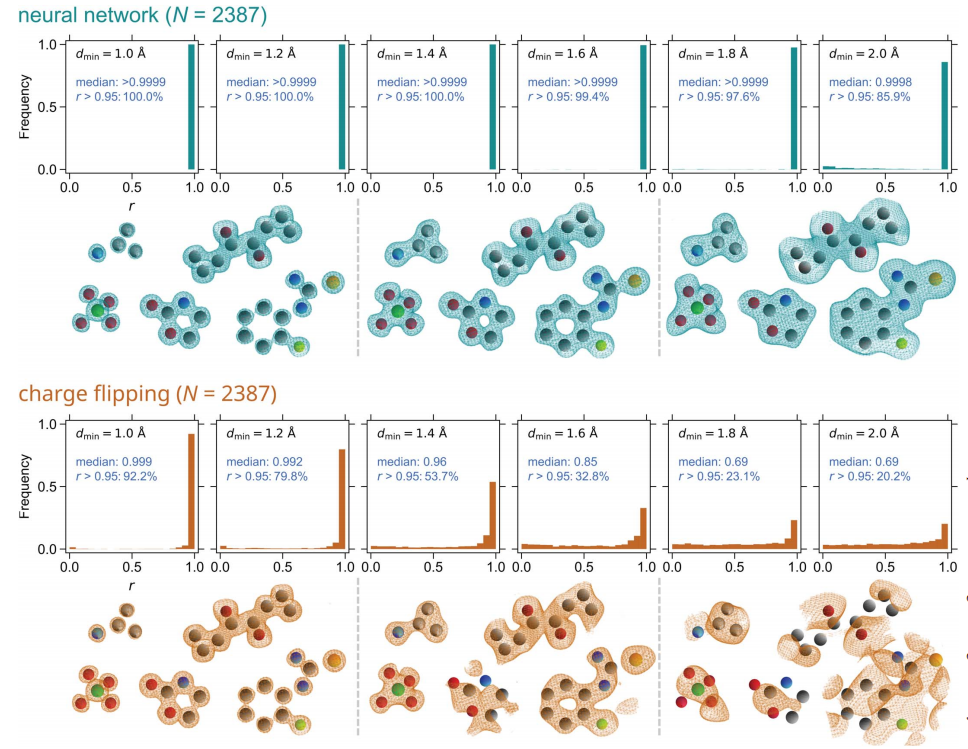
- Les chercheurs ont testé les performances du réseau neuronal en utilisant des données de diffraction calculées à partir de structures cristallines réelles. Au total, 2 387 cas de test ont été obtenus. Pour toutes les structures collectées, plusieurs valeurs de résolution de données allant de 1,0 à 2,0 Å ont été prises en compte. À titre de comparaison, une méthode d’inversion de charge a également été utilisée pour récupérer les informations de phase.
Illustration : Histogramme du coefficient de corrélation r entre la phase et la véritable carte de densité électronique.
(Source : article)
Le réseau neuronal entraîné fonctionne bien ; Il peut résoudre toutes les structures testées (N = 2387) si les données de diffraction correspondantes sont de bonne résolution, et est plus efficace pour résoudre des structures à partir de données basse résolution. Performance excellente. Bien qu’un réseau neuronal soit rarement formé sur des structures inorganiques, il peut parfaitement résoudre de telles structures.
La méthode d'inversion de charge fonctionne bien lors du traitement de données haute résolution, mais sa capacité à produire des solutions raisonnablement correctes diminue progressivement à mesure que la résolution des données diminue. Cependant, elle résout toujours environ 32 pixels à une résolution de 1,6Å % de structure ; Le nombre de structures identifiées par inversion de charge peut être amélioré par des expérimentations supplémentaires et par la modification des paramètres d'entrée tels que les seuils d'inversion.
Dans l'approche PhAI, cette méta-optimisation est réalisée lors de l'entraînement et n'a pas besoin d'être réalisée par l'utilisateur. Ces résultats suggèrent que la notion courante en cristallographie selon laquelle les données de résolution atomique sont nécessaires pour calculer les phases ab initio pourrait être brisée. La PhAI ne nécessite que 10 à 20 % de données de résolution atomique.
Ce résultat montre clairement que la résolution atomique n'est pas nécessaire pour les méthodes ab initio et ouvre de nouvelles voies pour la détermination de structure basée sur l'apprentissage profond.
Le défi de cette approche d'apprentissage en profondeur est de faire évoluer le réseau neuronal, c'est-à-dire que les données de diffraction pour des cellules unitaires plus grandes nécessiteront une grande quantité de données d'entrée et de sortie ainsi que des coûts de calcul pendant la formation. À l’avenir, des recherches supplémentaires seront nécessaires pour étendre cette méthode au cas général.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Articles Liés
Voir plus- Tendances technologiques à surveiller en 2023
- Comment l'intelligence artificielle apporte un nouveau travail quotidien aux équipes des centres de données
- L'intelligence artificielle ou l'automatisation peuvent-elles résoudre le problème de la faible efficacité énergétique des bâtiments ?
- Co-fondateur d'OpenAI interviewé par Huang Renxun : les capacités de raisonnement de GPT-4 n'ont pas encore atteint les attentes
- Bing de Microsoft surpasse Google en termes de trafic de recherche grâce à la technologie OpenAI