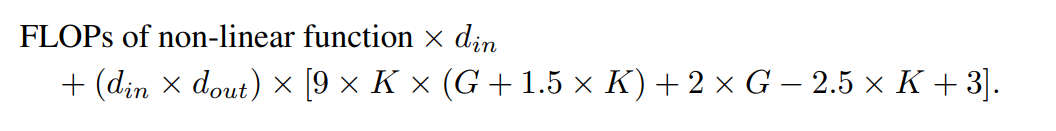Renversé? Dans un nouveau concours, KAN, qui prétend remplacer MLP, n'a remporté qu'un seul match

KAN est leader en représentation symbolique, mais MLP reste toujours généraliste.

Les perceptrons multicouches (MLP), également connus sous le nom de réseaux neuronaux à rétroaction entièrement connectés, sont un composant de base des modèles d'apprentissage profond d'aujourd'hui. L'importance du MLP ne peut être surestimée car il s'agit de la méthode par défaut pour approximer les fonctions non linéaires dans l'apprentissage automatique.

Cependant, MLP présente également certaines limites, telles que la difficulté d'interpréter les représentations apprises et la difficulté de faire évoluer de manière flexible la taille du réseau. L'émergence de

KAN (Kolmogorov-Arnold Networks) offre une alternative innovante au MLP traditionnel. Cette méthode surpasse le MLP en termes de précision et d’interprétabilité, et elle est capable de surpasser les MLP fonctionnant avec des tailles de paramètres beaucoup plus grandes et un très petit nombre de paramètres.

Alors, la question est : lequel dois-je choisir entre KAN et MLP ? Certaines personnes soutiennent MLP parce que KAN n'est qu'un MLP ordinaire et ne peut pas être remplacé du tout, mais d'autres pensent que KAN est supérieur. La comparaison actuelle entre les deux est également limitée à différents paramètres ou FLOP, et les résultats expérimentaux sont injustes.

Afin d'explorer le potentiel de KAN, il est nécessaire de comparer de manière exhaustive KAN et MLP dans un cadre équitable.

À cette fin, des chercheurs de l'Université nationale de Singapour ont formé et évalué KAN et MLP dans des tâches dans différents domaines, notamment la représentation de formules symboliques, l'apprentissage automatique, tout en contrôlant les paramètres ou FLOP de KAN et MLP, PNL et traitement audio. Dans ces paramètres équitables, ils ont constaté que KAN surpassait uniquement MLP sur la tâche de représentation de formule symbolique, tandis que MLP surpassait généralement KAN sur d'autres tâches.

• Adresse du papier : https://arxiv.org/pdf/2407.16674
• Lien du projet : https://github.com/yu-rp/KANbeFair
• Titre du papier : KAN ou MLP : Une comparaison plus juste

L'auteur a en outre découvert que L'avantage de KAN dans la représentation symbolique des formules découle de son utilisation de la fonction d'activation B-spline. Initialement, les performances globales de MLP étaient en retard par rapport à KAN, mais après avoir remplacé la fonction d'activation de MLP par des B-splines, ses performances ont égalé ou même dépassé KAN. Cependant, les B-splines ne peuvent pas améliorer davantage les performances du MLP sur d'autres tâches telles que la vision par ordinateur.

Les auteurs ont également constaté que KAN ne fonctionnait pas mieux que MLP sur les tâches d'apprentissage continu. L'article original du KAN comparait les performances du KAN et du MLP sur une tâche d'apprentissage continu utilisant une série de fonctions unidimensionnelles, où chaque fonction suivante est une traduction de la fonction précédente le long de l'axe des nombres. Cet article compare les performances de KAN et MLP dans un cadre d’apprentissage continu incrémentiel de classe plus standard. Dans des conditions d’itération d’entraînement fixes, ils ont découvert que le problème d’oubli de KAN était plus grave que celui de MLP.

KAN, brève introduction de MLP

KAN a deux branches, la première branche est la branche B-spline et l'autre branche est la branche de raccourci, c'est-à-dire que l'activation non linéaire et la transformation linéaire sont connectés ensemble. Dans l'implémentation officielle, la branche raccourcie est une fonction SiLU suivie d'une transformation linéaire. Soit x représente le vecteur caractéristique d'un échantillon. Ensuite, l'équation directe de la branche spline KAN peut s'écrire comme suit :

Dans l'architecture KAN originale, la fonction spline est choisie comme fonction B-spline. Les paramètres de chaque fonction B-spline sont appris avec les autres paramètres du réseau.

En conséquence, l'équation directe du MLP monocouche peut être exprimée comme suit :

Cette formule a la même forme que la formule de branche B-spline dans KAN, sauf qu'elle diffère par la fonction non linéaire . Par conséquent, quelle que soit l’interprétation de la structure KAN donnée par l’article original, KAN peut également être considéré comme une couche entièrement connectée.

Par conséquent, il existe deux différences principales entre KAN et MLP ordinaire :

1. La fonction d'activation est différente. Habituellement, la fonction d'activation dans MLP inclut ReLU, GELU, etc., qui n'ont pas de paramètres apprenables et sont uniformes pour tous les éléments d'entrée. Dans KAN, la fonction d'activation est une fonction spline avec des paramètres apprenables, et pour chaque entrée, les éléments sont tous différents. .
2. Séquence d'opérations linéaires et non linéaires.一般來說，研究者會把 MLP 概念化為先進行線性變換，再進行非線性變換，而 KAN 其實是先進行非線性變換，再進行線性變換。但在某種程度上，將 MLP 中的全連接層描述為先非線性，後線性也是可行的。

透過比較 KAN 和 MLP，研究認為兩者之間的差異主要是活化函數。因而，他們假設活化函數的差異使得 KAN 和 MLP 適用於不同的任務，導致兩個模型在功能上有差異。為了驗證這個假設，研究者比較了 KAN 和 MLP 在不同任務上的表現，並描述了每個模型適合的任務。為了確保公平比較，研究首先推導出了計算 KAN 和 MLP 參數數量和 FLOP 的公式。實驗過程控制相同數量的參數或 FLOP 來比較 KAN 和 MLP 的表現。

KAN 和MLP 的參數數量及FLOP 

控制參數數量

KAN 中可學習的參數包括B 樣條控制點、shortcut 權重、B 樣條權重和偏置項。總的可學習參數數量為：

其中， d_in 和d_out 表示神經網路層的輸入和輸出維度，K 表示樣條的階數，它與官方nn.Module KANLayer 的參數k 相對應，它是樣條函數中多項式基礎的階數。 G 表示樣條間隔數，它對應於官方 nn.Module KANLayer 的 num 參數。它是填充前 B 樣條曲線的間隔數。在填充之前，它等於控制點的數量 - 1。在填充後，應該有 (K +G) 個有效控制點。

相應的，一個MLP 層的可學習參數是：

KAN 和MLP 的FLOP

而布林操作的FLOP 被考慮為0。 De Boor-Cox 演算法中的 0 階操作可以轉換為一系列布林操作，這些操作不需要進行浮點運算。因此，從理論上講，其 FLOP 為 0。這與官方 KAN 實作不同，在官方實作中，它將布林資料轉換回浮點資料來進行操作。

在作者的評估中，FLOP 是針對一個樣本計算的。官方KAN 程式碼中使用De Boor-Cox 迭代公式實現的B 樣條FLOP 為：

連同shortcut 路徑的FLOP 以及合併兩個分支的FLOP，一個KAN 層的總FLOP 是：

對應的，一個MLP 層的FLOP 為：

具有相同輸入維度和輸出維度的KAN 層與MLP 層之間的FLOP 差異可以表示為：

如果MLP 也首先進行非線性操作，那麼首項將為零。

 實驗

作者的目標是，在參數數量或 FLOP 相等的前提下，對比 KAN 和 MLP 的表現差異。本實驗涵蓋多個領域，包括機器學習、電腦視覺、自然語言處理、音訊處理以及符號公式表示。所有實驗都採用了 Adam 優化器，這些實驗全部在一塊 RTX3090 GPU 上進行。

性能比較

🎜🎜🎜🎜機器學習。作者在 8 個機器學習資料集上進行了實驗，使用了具有一到兩個隱藏層的 KAN 和 MLP，根據各個資料集的特點，他們調整了神經網路的輸入和輸出維度。 🎜🎜🎜🎜🎜對於 MLP，隱藏層寬度設定為 32、64、128、256、512 或 1024，並採用 GELU 或 ReLU 作為活化函數，同時在 MLP 中使用了歸一化層。對於 KAN，隱藏層寬度則為 2、4、8 或 16，B 樣條網格數為 3、5、10 或 20，B 樣條的度數（degree）為 2、3 或 5。

由於原始 KAN 架構不包括歸一化層，為了平衡 MLP 中歸一化層可能帶來的優勢，作者擴大了 KAN 樣條函數的取值範圍。所有實驗都進行了 20 輪訓練，實驗記錄了訓練過程中在測試集上取得的最佳準確率，如圖 2 和圖 3 所示。

在機器學習資料集上，MLP 通常保持優勢。在他們對八個資料集的實驗中，MLP 在其中的六個上表現優於 KAN。然而，他們也觀察到在一個資料集上，MLP 和 KAN 的表現幾乎相當，而在另一個資料集上，KAN 表現則優於 MLP。

整體而言，MLP 在機器學習資料集上仍具有普遍優勢。

電腦視覺。作者對 8 個電腦視覺資料集進行了實驗。他們使用了具有一到兩個隱藏層的 KAN 和 MLP，根據資料集的不同，調整了神經網路的輸入和輸出維度。

在電腦視覺資料集中，KAN 的樣條函數引入的處理偏差並沒有起到效果，其性能始終不如具有相同參數數量或 FLOP 的 MLP。

音訊和自然語言處理。作者在 2 個音訊分類和 2 個文字分類資料集上進行了實驗。他們使用了一到兩個隱藏層的 KAN 和 MLP，並根據資料集的特性，調整了神經網路的輸入和輸出維度。

在兩個音訊資料集上，MLP 的表現優於 KAN。

在文字分類任務中，MLP 在 AG 新聞資料集上保持了優勢。然而，在 CoLA 資料集上，MLP 和 KAN 之間的表現沒有顯著差異。當控制參數數量相同時，KAN 在 CoLA 資料集上似乎有優勢。然而，由於 KAN 的樣條函數需要較高的 FLOP，因此此優勢在控制 FLOP 的實驗中並未持續顯現。當控制 FLOP 時，MLP 似乎更勝一籌。因此，在 CoLA 資料集上，並沒有一個明確的答案來說明哪種模型更好。

總體而言，MLP 在音訊和文字任務中仍然是更好的選擇。

符號公式表示。作者在 8 個符號公式表示任務中比較了 KAN 和 MLP 的差異。他們使用了一到四個隱藏層的 KAN 和 MLP，根據資料集調整了神經網路的輸入和輸出維度。

在控制參數數量的情況下，KAN 在 8 個資料集中的 7 個上表現優於 MLP。在控制 FLOP 時，由於樣條函數引入了額外的計算複雜性，KAN 的效能大致與 MLP 相當，在兩個資料集上優於 MLP，在另一個資料集上表現不如 MLP。

整體而言，在符號公式表示任務中，KAN 的表現優於 MLP。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!