Maison >Java >javaDidacticiel >Test de la classe AVLTree
Test de la classe AVLTree
- 王林original
- 2024-07-25 09:09:31784parcourir
Cette section donne un exemple d'utilisation de la classe AVLTree. Le code ci-dessous donne un programme de test. Le programme crée un AVLTree initialisé avec un tableau d'entiers 25, 20 et 5 (lignes 7), insère des éléments dans lignes 11 à 20 et supprime les éléments des lignes 24 à 30. Puisque AVLTree est une sous-classe de BST et que les éléments d'un BST sont itérables, le programme utilise une boucle foreach pour parcourir tous les éléments des lignes 35 à 37. .
package demo;
public class TestAVLTree {
public static void main(String[] args) {
// Create an AVL tree
AVLTree<Integer> tree = new AVLTree<>(new Integer[]{25, 20, 5});
System.out.print("After inserting 25, 20, 5:");
printTree(tree);
tree.insert(34);
tree.insert(50);
System.out.print("\nAfter inserting 34, 50:");
printTree(tree);
tree.insert(30);
System.out.print("\nAfter inserting 30");
printTree(tree);
tree.insert(10);
System.out.print("\nAfter inserting 10");
printTree(tree);
tree.delete(34);
tree.delete(30);
tree.delete(50);
System.out.print("\nAfter removing 34, 30, 50:");
printTree(tree);
tree.delete(5);
System.out.print("\nAfter removing 5:");
printTree(tree);
System.out.print("\nTraverse the elements in the tree: ");
for (int e: tree) {
System.out.print(e + " ");
}
}
public static void printTree(BST tree) {
// Traverse tree
System.out.print("\nInorder (sorted): ");
tree.inorder();
System.out.print("\nPostorder: ");
tree.postorder();
System.out.print("\nPreorder: ");
tree.preorder();
System.out.print("\nThe number of nodes is " + tree.getSize());
System.out.println();
}
}
Après avoir inséré 25, 20, 5 :
En commande (triés) : 5 20 25
Postcommande : 5 25 20
Précommande : 20 5 25
Le nombre de nœuds est de 3
Après avoir inséré 34, 50 :
En commande (triés) : 5 20 25 34 50
Postcommande : 5 25 50 34 20
Précommande : 20 5 34 25 50
Le nombre de nœuds est de 5
Après avoir inséré 30
En commande (triés) : 5 20 25 30 34 50
Postcommande : 5 20 30 50 34 25
Précommande : 25 20 5 34 30 50
Le nombre de nœuds est de 6
Après avoir inséré 10
En commande (triés) : 5 10 20 25 30 34 50
Postcommande : 5 20 10 30 50 34 25
Précommande : 25 10 5 20 34 30 50
Le nombre de nœuds est de 7
Après avoir supprimé 34, 30, 50 :
En commande (triés) : 5 10 20 25
Postcommande : 5 20 25 10
Précommande : 10 5 25 20
Le nombre de nœuds est de 4
Après avoir supprimé 5 :
En commande (triés) : 10 20 25
Postcommande : 10 25 20
Précommande : 20 10 25
Le nombre de nœuds est de 3
Parcourir les éléments dans l'arbre : 10 20 25
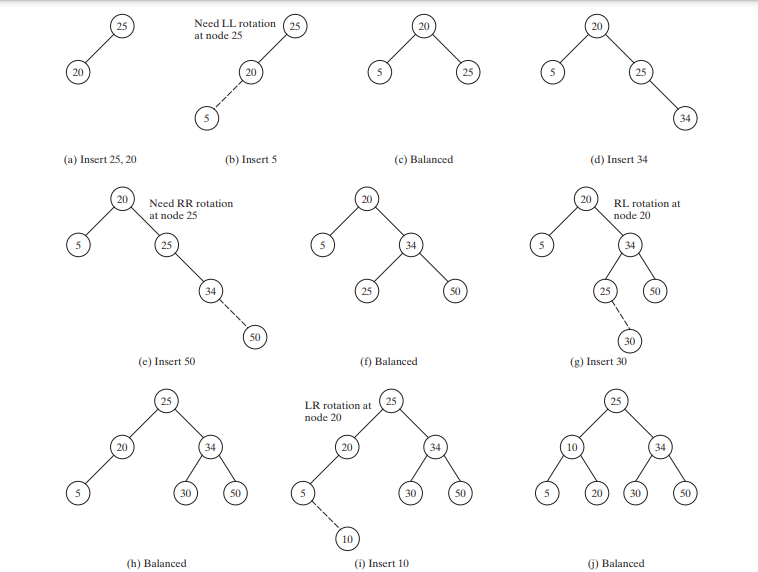
La figure ci-dessous montre comment l'arbre évolue à mesure que des éléments sont ajoutés à l'arbre. Une fois 25 et 20 ajoutés, l'arbre se présente comme le montre la figure ci-dessous (a). 5 est inséré comme enfant gauche de 20 ans, comme le montre la figure ci-dessous (b). L'arbre n'est pas équilibré. Il est lourd à gauche au nœud 25. Effectuez une rotation LL pour obtenir un arbre AVL, comme le montre la figure ci-dessous (c).
Après avoir inséré 34, l'arbre est représenté dans la figure ci-dessous (d). Après avoir inséré 50, l’arbre se présente comme indiqué dans la figure ci-dessous (e). L'arbre n'est pas équilibré. Il est lourd à droite au nœud 25. Effectuez une rotation RR pour obtenir un arbre AVL, comme le montre la figure ci-dessous (f).
Après avoir inséré 30, l'arbre se présente comme indiqué dans la figure ci-dessous (g). L'arbre n'est pas équilibré. Effectuez une rotation RL pour obtenir un arbre AVL, comme le montre la figure ci-dessous (h).
Après avoir inséré 10, l'arbre est comme indiqué dans la figure ci-dessous (i). L'arbre n'est pas équilibré. Effectuez une rotation LR pour obtenir un arbre AVL, comme le montre la figure ci-dessous (j).
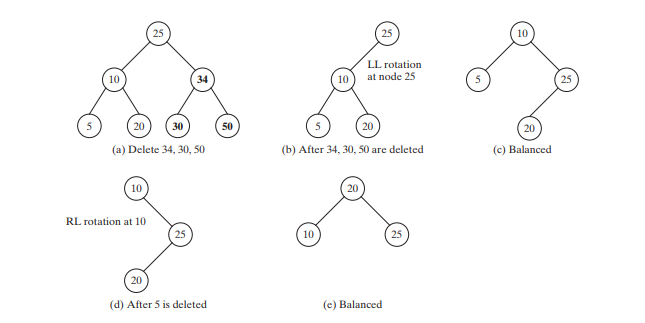
La figure ci-dessous montre comment l'arborescence évolue à mesure que des éléments sont supprimés. Après avoir supprimé 34, 30 et 50, l’arborescence ressemble à la figure ci-dessous (b). L'arbre n'est pas équilibré. Effectuez une rotation LL pour obtenir un arbre AVL, comme indiqué dans la figure ci-dessous (c).
Après avoir supprimé 5, l'arbre est tel qu'illustré dans la figure ci-dessous (d). L'arbre n'est pas équilibré. Effectuez une rotation RL pour obtenir un arbre AVL, comme indiqué dans la figure ci-dessous (e)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

