Déjouer tous les pronostics : les mathématiques derrière les bénéfices des casinos

Vous êtes-vous déjà demandé pourquoi les casinos semblent toujours gagner ? Dans «  Battre toutes les chances : les mathématiques derrière les bénéfices des casinos  », nous explorerons les mathématiques simples et les stratégies intelligentes qui garantissent que les casinos gagnent de l'argent à long terme. À travers des exemples faciles à comprendre et des simulations de Monte Carlo, nous vous dévoilerons les secrets qui se cachent derrière les contours de la maison. Préparez-vous à découvrir comment les casinos font tourner les chances en leur faveur !

Comprendre l'avantage de la maison

L'avantage de la maison est une notion fondamentale dans le monde des casinos. Il représente le profit moyen que le casino espère réaliser sur chaque pari placé par les joueurs. Essentiellement, c'est le pourcentage de chaque pari que le casino conservera à long terme.

L'avantage de la maison existe parce que les casinos ne paient pas les paris gagnants en fonction des « vraies cotes » du jeu. Les vraies cotes représentent la probabilité réelle qu'un événement se produise. En payant à des cotes légèrement inférieures, les casinos s'assurent de réaliser des bénéfices au fil du temps.

L'avantage de la maison (HE) est défini comme le profit du casino exprimé en pourcentage de la mise initiale du joueur.

** La Roulette Européenne ** n'a qu'un seul zéro vert, ce qui lui donne 37 numéros au total. Si un joueur parie 1 $ sur le rouge, il a 18 chances sur 37 de gagner 1 $ et 19 chances sur 37 de perdre 1 $. La valeur attendue est :

Valeur attendue=( 1 × 18/37 ​)+( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2,7%

Par conséquent, à la roulette européenne, l'avantage de la maison (HE) est d'environ 2,7 %

Créons notre propre jeu pour mieux le comprendre, un jeu de lancer de dés simple.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll <= 50:
        print(roll, 'You rolled between 1 and 50 and lost.')
        return False
    else:
        print(roll, 'You rolled between 51 and 99 and won! Keep playing!')
        return True

Dans ce jeu :

• Le joueur a 1/100 de chance de perdre si le résultat est 100.

• Le joueur a 50/100 de chances de perdre si le jet est compris entre 1 et 50.

• Le joueur a 49/100 de chances de gagner si le jet est compris entre 51 et 99.

Valeur attendue =(1× 49/100​) + ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

Par conséquent, l'avantage de la maison est de 2%.

Comprendre la simulation de Monte Carlo

Les simulations de Monte Carlo sont un outil puissant utilisé pour comprendre et prédire des systèmes complexes en exécutant de nombreuses simulations d'un processus et en observant les résultats. Dans le contexte des casinos, les simulations Monte Carlo peuvent modéliser divers scénarios de paris pour montrer comment l'avantage de la maison garantit la rentabilité à long terme. Explorons comment fonctionnent les simulations de Monte Carlo et comment elles peuvent être appliquées à un simple jeu de casino.

Qu’est-ce qu’une simulation Monte-Carlo ?

Une simulation Monte Carlo consiste à générer des variables aléatoires pour simuler un processus plusieurs fois et à analyser les résultats. En effectuant des milliers, voire des millions d'itérations, nous pouvons obtenir une distribution des résultats possibles et avoir un aperçu de la probabilité de différents événements.

Application de la simulation de Monte Carlo au jeu de lancer de dés

Nous utiliserons une simulation de Monte Carlo pour modéliser le jeu de lancer de dés dont nous avons parlé plus tôt. Cela nous aidera à comprendre comment l’avantage de la maison affecte la rentabilité du jeu au fil du temps.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins += 1
        else:
            losses += 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

Interprétation des résultats

Dans cette simulation, nous exécutons le jeu de lancer de dés 10 000 000 de fois pour observer les pourcentages de victoires et de pertes. Compte tenu de l'avantage de la maison calculé précédemment (2 %), nous nous attendons à ce que le pourcentage de perte soit légèrement supérieur au pourcentage de victoire.

Après avoir exécuté la simulation, vous pourriez voir des résultats tels que :

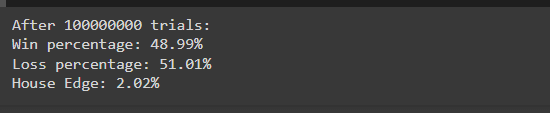
Ces résultats s'alignent étroitement sur les probabilités théoriques (49 % de victoire, 51 % de perte), démontrant comment l'avantage de la maison se manifeste sur un grand nombre d'essais. Le léger déséquilibre assure la rentabilité du casino à long terme.

Visualiser les gains à court terme et les pertes à long terme

Les simulations Monte Carlo sont puissantes pour modéliser et prédire les résultats grâce à un échantillonnage aléatoire répété. Dans le contexte du jeu, nous pouvons utiliser les simulations de Monte Carlo pour comprendre les résultats potentiels de différentes stratégies de paris.

Nous simulerons un seul parieur qui place la même mise initiale à chaque tour et observerons comment la valeur de son compte évolue sur un nombre spécifié de mises.

Voici comment simuler et visualiser le parcours de pari à l'aide de Matplotlib :

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager <= wager_count:
        if roll_dice():
            value += wager
        else:
            value -= wager

        wX.append(current_wager)
        vY.append(value)
        current_wager += 1

    return wX, vY

# Parameters for simulation
funds = 10000
initial_wager = 100
wager_count = 1000

# Run the simulation for a single bettor
wager_counts, account_values = bettor_simulation(funds, initial_wager, wager_count)

# Plotting the results
plt.figure(figsize=(12, 6))
plt.plot(wager_counts, account_values, label='Bettor 1', color='blue')
plt.xlabel('Wager Count')
plt.ylabel('Account Value')
plt.title('Betting Journey: Short-Term Wins vs Long-Term Losses')
plt.grid(True)
plt.legend()

# Highlighting the short-term and long-term trend
plt.axhline(y=funds, color='gray', linestyle='--', label='Initial Funds')
plt.axhline(y=account_values[0], color='green', linestyle='--', label='Starting Account Value')
plt.axhline(y=account_values[-1], color='red', linestyle='--', label='Final Account Value')

plt.legend()
plt.show()

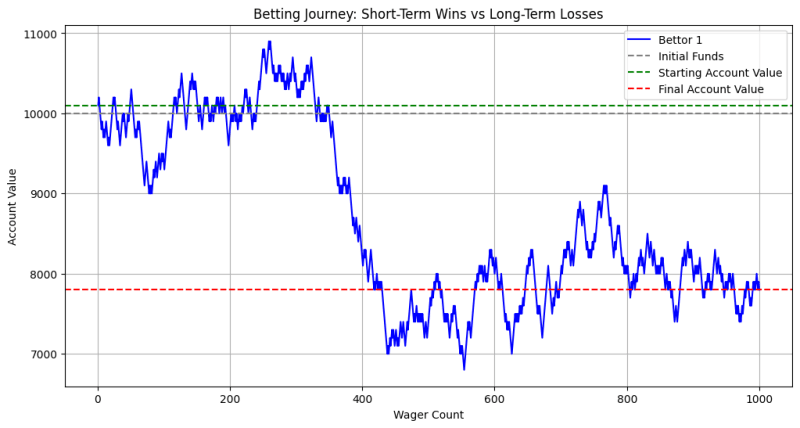
Ce graphique illustre comment la valeur du compte d’un parieur peut fluctuer au fil du temps en raison des gains et des pertes. Au début, il peut y avoir des périodes de gains (ligne verte au-dessus de la valeur de départ), mais à mesure que le nombre de mises augmente, l'effet cumulatif de l'avantage de la maison devient évident. Finalement, la valeur du compte du parieur a tendance à baisser vers ou en dessous des fonds initiaux (ligne grise), indiquant des pertes à long terme.

Conclusion

Comprendre les mathématiques derrière les bénéfices du casino révèle un net avantage pour la maison dans chaque jeu grâce au concept de l'avantage de la maison. Malgré des gains occasionnels, la probabilité intégrée aux jeux de casino garantit que la plupart des joueurs perdront de l'argent au fil du temps. Les simulations de Monte Carlo illustrent de manière frappante cette dynamique, montrant comment même les gains à court terme peuvent masquer les pertes à long terme dues à l’avantage statistique du casino. Cet aperçu de la certitude mathématique de la rentabilité des casinos souligne l’importance d’une prise de décision éclairée et de pratiques de jeu responsables.

Ensuite, nous pourrions explorer des visualisations ou des variations supplémentaires, telles que la comparaison de différentes stratégies de paris ou l'analyse de l'impact de différentes mises initiales sur les résultats du parieur.

Restez connecté :

• GitHub : ezhillragesh

• Twitter : ezhillragesh

• Site Web : ragesh.me

N'hésitez pas à partager vos réflexions, à poser des questions et à contribuer à la discussion.

Bon codage !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!