Résoudre le problème des huit reines en utilisant le retour en arrière

Le problème des huit reines est de trouver une solution pour placer une reine dans chaque rangée d'un échiquier de telle sorte que deux reines ne puissent pas s'attaquer. Le problème peut être résolu en utilisant la récursivité. Dans cette section, nous présenterons une technique de conception d'algorithmes courante appelée backtracking pour résoudre ce problème. L'approche de backtracking recherche progressivement une solution candidate, abandonnant cette option dès qu'elle détermine que la
Le candidat ne peut pas être une solution valable, puis cherche un nouveau candidat.

Vous pouvez utiliser un tableau bidimensionnel pour représenter un échiquier. Cependant, comme chaque ligne ne peut avoir qu'une seule reine, il suffit d'utiliser un tableau unidimensionnel pour désigner la position de la reine dans la ligne. Ainsi, vous pouvez définir le tableau queens comme :

int[] reines = new int[8];

Attribuez j aux reines[i] pour indiquer qu'une reine est placée dans la ligne i et la colonne j. La figure ci-dessous (a) montre le contenu du tableau reines pour l'échiquier de la figure ci-dessous (b).

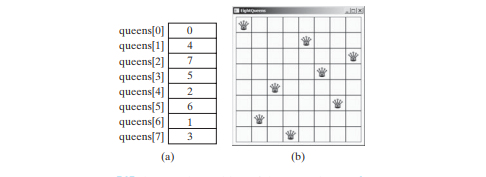
La recherche commence à partir de la première ligne avec k = 0, où k est l'index de la ligne actuelle considérée. L'algorithme vérifie si une reine peut éventuellement être placée dans la j_ième colonne de la ligne pour _j = 0, 1, ..., 7, dans cet ordre. La recherche s'effectue comme suit :

• En cas de succès, il continue à chercher un emplacement pour une reine dans la rangée suivante. Si la ligne actuelle est la dernière ligne, une solution est trouvée.
• En cas d'échec, il revient à la ligne précédente et continue de rechercher un nouvel emplacement dans la colonne suivante de la ligne précédente.
• Si l'algorithme revient à la première rangée et ne parvient pas à trouver un nouvel emplacement pour une reine dans cette rangée, aucune solution ne peut être trouvée.

Le code ci-dessous donne le programme qui affiche une solution au problème des Huit Reines.

package application;
import javafx.application.Application;
import javafx.geometry.Pos;
import javafx.stage.Stage;
import javafx.scene.Scene;
import javafx.scene.control.Label;
import javafx.scene.image.Image;
import javafx.scene.image.ImageView;
import javafx.scene.layout.GridPane;

public class EightQueens extends Application {
    public static final int SIZE = 8; // The size of the chess board
    // queens are placed at (i, queens[i])
    // -1 indicates that no queen is currently placed in the ith row
    // Initially, place a queen at (0, 0) in the 0th row
    private int[] queens = {-1, -1, -1, -1, -1, -1, -1, -1};

    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        search(); // Search for a solution

        // Display chess board
        GridPane chessBoard = new GridPane();
        chessBoard.setAlignment(Pos.CENTER);
        Label[][] labels = new Label[SIZE][SIZE];
        for(int i = 0; i < SIZE; i++)
            for(int j = 0; j < SIZE; j++) {
                chessBoard.add(labels[i][j] = new Label(), i, j);
                labels[i][j].setStyle("-fx-border-color: black");
                labels[i][j].setPrefSize(55, 55);
            }

        // Display queens
        Image image = new Image("file:C:/Users/Paul/development/MyJavaFX/src/application/image/lo.jpg");
        for(int i = 0; i < SIZE; i++)
            labels[i][queens[i]].setGraphic(new ImageView(image));

        // Create a scene and place it in the stage
        Scene scene = new Scene(chessBoard, 55 * SIZE, 55 * SIZE);
        primaryStage.setTitle("EightQueens"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Search for a solution */
    private boolean search() {
        // k - 1 indicates the number of queens placed so far
        // We are looking for a position in the kth row to place a queen
        int k = 0;
        while(k >= 0 && k < SIZE) {
            // Find a position to place a queen in the kth row
            int j = findPosition(k);
            if(j < 0) {
                queens[k] = -1;
                k--; // back track to the previous row
            } else {
                queens[k] = j;
                k++;
            }
        }

        if(k == -1)
            return false; // No solution
        else
            return true; // A solution is found
    }

    public int findPosition(int k) {
        int start = queens[k] + 1; // Search for a new placement

        for(int j =start; j < SIZE; j++) {
            if(isValid(k, j))
                return j; // (k, j) is the place to put the queen now
        }

        return -1;
    }

    /** Return true is a queen can be placed at (row, column) */
    public boolean isValid(int row, int column) {
        for(int i = 1; i <= row; i++)
            if(queens[row - i] == column // Check column
            || queens[row - i] == column - i // Check upleft diagonal
            || queens[row - i] == column + i) // Check upright diagonal
                return false; // There is a conflict
        return true; // No conflict
    }

}

Le programme invoque search() (ligne 20) pour rechercher une solution. Initialement, aucune reine n'est placée dans aucune rangée (ligne 16). La recherche commence maintenant à partir de la première ligne avec k = 0 (ligne 53) et trouve une place pour la reine (ligne 56). En cas de succès, placez-le dans la ligne (ligne 61) et considérez la ligne suivante (ligne 62). En cas d'échec, revenez à la ligne précédente (lignes 58 à 59).

La méthode findPosition(k) recherche une position possible pour placer une reine dans la rangée k à partir de queen[k] + 1 (ligne 73 ). Il vérifie si une reine peut être placée à start, start + 1, . . . , et 7, dans cet ordre (lignes 75 à 78). Si possible, renvoyez l'index de la colonne (ligne 77); sinon, retournez -1 (ligne 80).

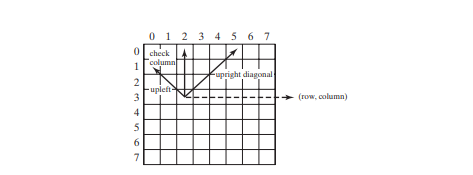
La méthode isValid(row, column) est appelée pour vérifier si le fait de placer une reine à la position spécifiée provoque un conflit avec les reines placées plus tôt (ligne 76). Cela garantit qu'aucune reine n'est placée dans la même colonne (ligne 86), dans la diagonale supérieure gauche (ligne 87) ou dans la diagonale supérieure droite (ligne 88), comme le montre la figure ci-dessous.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!