Tous les ancêtres d'un nœud dans un graphe acyclique dirigé

2192. Tous les ancêtres d'un nœud dans un graphe acyclique dirigé

Moyen

Vous recevez un entier positif n représentant le nombre de nœuds d'un Graphique acyclique dirigé (DAG). Les nœuds sont numérotés de 0 à n - 1 (inclus).

Vous recevez également un tableau d'entiers 2D Edges, où Edges[i] = [from_i, to_i] indique qu'il existe un unidirectionnel bord de_i à à_i dans le graphique.

Renvoie une réponse de liste, où réponse[i] est la liste des ancêtres du i^ème nœud, triés par ordre croissant.

Un nœud u est un ancêtre d'un autre nœud v si vous pouvez atteindre v via un ensemble d'arêtes.

Exemple 1 :

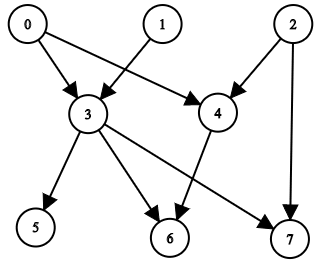
• Entrée : n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5] ,[3,6],[3,7],[4,6]]
• Sortie : [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4], [0,1,2,3]]
• Explication : Le diagramme ci-dessus représente le graphique d'entrée.
  • Les nœuds 0, 1 et 2 n'ont aucun ancêtre.
  • Le nœud 3 a deux ancêtres 0 et 1.
  • Le nœud 4 a deux ancêtres 0 et 2.
  • Le nœud 5 a trois ancêtres 0, 1 et 3.
  • Le nœud 6 a cinq ancêtres 0, 1, 2, 3 et 4.
  • Le nœud 7 a quatre ancêtres 0, 1, 2 et 3.

Exemple 2 :

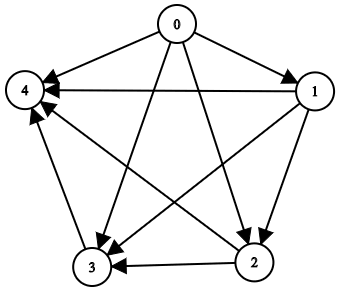
• Entrée : n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3] ,[1,4],[2,3],[2,4],[3,4]]
• Sortie : [[],[0],[0,1],[0,1,2],[0,1,2,3]]
• Explication : Le diagramme ci-dessus représente le graphique d'entrée.
  • Le nœud 0 n'a aucun ancêtre.
  • Le nœud 1 a un ancêtre 0.
  • Le nœud 2 a deux ancêtres 0 et 1.
  • Le nœud 3 a trois ancêtres 0, 1 et 2.
  • Le nœud 4 a quatre ancêtres 0, 1, 2 et 3.

Contraintes :

• 1 <= n <= 1000
• 0 <= bords.longueur <= min(2000, n * (n - 1) / 2)
• bords[i].length == 2
• 0 <= de_i, à_i <= n - 1
• de_i != à_i
• Il n'y a pas de bords en double.
• Le graphe est orienté et acyclique.

Solution :

class Solution {

    /**
     * @param Integer $n
     * @param Integer[][] $edges
     * @return Integer[][]
     */
    function getAncestors($n, $edges) {
        $adjacencyList = array_fill(0, $n, []);
        foreach ($edges as $edge) {
            $from = $edge[0];
            $to = $edge[1];
            $adjacencyList[$to][] = $from;
        }

        $ancestorsList = [];

        for ($i = 0; $i < $n; $i++) {
            $ancestors = [];
            $visited = [];
            $this->findChildren($i, $adjacencyList, $visited);
            for ($node = 0; $node < $n; $node++) {
                if ($node == $i) continue;
                if (in_array($node, $visited))
                    $ancestors[] = $node;
            }
            $ancestorsList[] = $ancestors;
        }

        return $ancestorsList;
    }

    private function findChildren($currentNode, &$adjacencyList, &$visitedNodes) {
        $visitedNodes[] = $currentNode;
        foreach ($adjacencyList[$currentNode] as $neighbour) {
            if (!in_array($neighbour, $visitedNodes)) {
                $this->findChildren($neighbour, $adjacencyList, $visitedNodes);
            }
        }
    }
}




Liens de contact


LinkedIn
GitHub



          

            
  

            
        
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!