Trouver des nombres de Fibonacci à l'aide de la programmation dynamique

Cette section analyse et conçoit un algorithme efficace pour trouver les nombres de Fibonacci à l'aide de la programmation dynamique. La section 18.3, Étude de cas : Calcul des nombres de Fibonacci, a donné une méthode récursive pour trouver le nombre de Fibonacci, comme suit :

/**La méthode pour trouver le nombre de Fibonacci*/
public statique long fib (index long) {
if (index == 0) // Cas de base
renvoie 0 ;
sinon if (index == 1) // Cas de base
renvoie 1 ;
else // Réduction et appels récursifs
return fib(index - 1) + fib(index - 2);
>

Nous pouvons maintenant prouver que la complexité de cet algorithme est O(2^n). Pour plus de commodité, soit l'indice n. Soit T(n) la complexité de l'algorithme qui trouve fib(n) et c désigne le temps constant pour comparer l'indice avec 0 et 1 ; c'est-à-dire que T(1) et T(0) sont c. Ainsi,

Similaire à l'analyse du problème de la Tour de Hanoï, nous pouvons montrer que T(n) est O(2^n).

Cependant, cet algorithme n’est pas efficace. Existe-t-il un algorithme efficace pour trouver un nombre de Fibonacci ? Le problème avec la méthode récursive fib est que la méthode est invoquée de manière redondante avec les mêmes arguments. Par exemple, pour calculer fib(4), fib(3) et fib(2) sont invoqués. Pour calculer fib(3), fib(2) et fib(1) sont invoqués. Notez que fib(2) est invoqué de manière redondante. Nous pouvons l'améliorer en évitant d'appeler à plusieurs reprises la méthode fib avec le même argument. Notez qu'un nouveau nombre de Fibonacci est obtenu en additionnant les deux nombres précédents dans la séquence. Si vous utilisez les deux variables f0 et f1 pour stocker les deux nombres précédents, le nouveau nombre, f2, peut être immédiatement obtenu en ajoutant f0 avec f1. Vous devez maintenant mettre à jour f0 et f1 en attribuant f1 à f0 et en attribuant f2 à f1 , comme le montre la figure ci-dessous.

La nouvelle méthode est implémentée dans le code ci-dessous.

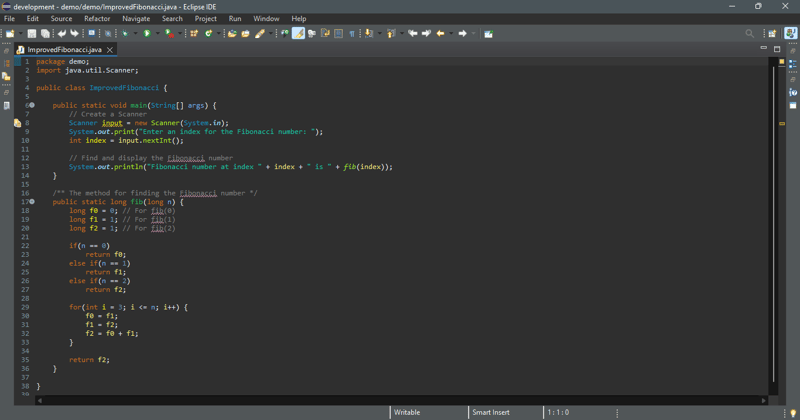
Entrez un indice pour le nombre de Fibonacci : 6
Le nombre de Fibonacci à l'indice 6 est 8

Entrez un indice pour le nombre de Fibonacci : 7
Le nombre de Fibonacci à l'indice 7 est 13

Évidemment, la complexité de ce nouvel algorithme est O(n). Il s'agit d'une amélioration considérable par rapport à l'algorithme récursif O(2^n).

L'algorithme de calcul des nombres de Fibonacci présenté ici utilise une approche connue sous le nom de programmation dynamique. La programmation dynamique est le processus de résolution de sous-problèmes, puis de combinaison des solutions des sous-problèmes pour obtenir une solution globale. Cela conduit naturellement à une solution récursive. Cependant, il serait inefficace d’utiliser la récursion, car les sous-problèmes se chevauchent. L'idée clé derrière la programmation dynamique est de résoudre chaque sous-problème une seule fois et de stocker les résultats des sous-problèmes pour une utilisation ultérieure afin d'éviter le calcul redondant des sous-problèmes.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!