 Technology peripherals
Technology peripherals AI
AI A relay spanning more than 300 years: Inspired by Terence Teru, mathematicians decided to use AI to formalize the proof of Fermat's Last Theorem.
A relay spanning more than 300 years: Inspired by Terence Teru, mathematicians decided to use AI to formalize the proof of Fermat's Last Theorem.Inspired by Terence Tao, more and more mathematicians are beginning to try to use artificial intelligence for mathematical exploration. This time, their target is Fermat's Last Theorem, one of the world's top ten most difficult mathematical problems. Fermat's Last Theorem is a very complex mathematical problem for which no feasible solution has been found so far. Mathematicians hope that with the help of artificial intelligence's powerful computing power and intelligent algorithms, they can explore in mathematics

Fermat's Last Theorem is also known as "Fermat's Last Theorem" Last Theorem (FLT)" was proposed by the 17th-century French mathematician Pierre de Fermat. There is a legendary story behind it. It is said that around 1637, when Fermat was reading the Latin translation of Diophantus' Arithmetic, he wrote next to Proposition 8 of Volume 11: "Divide a cubic number into the sum of two cubic numbers, or It is impossible to divide a fourth power into the sum of two fourth powers, or generally a power higher than the second power into the sum of two powers of the same power. "I am convinced that I have discovered something about this. This is a wonderful demonstration, but unfortunately the blank space here is too small to write it down. ”

What is stated before this paragraph is the content of Fermat’s last theorem: when the integer n>2, the equation about x^n y^n=z^n There is no positive integer solution.
Fermat said that he knew how to prove it, but because the blank part of the book was too small, he did not write about the authenticity of the story and whether Fermat really figured out the proof method. , it is controversial in later generations. For more than 300 years, mathematicians have been working hard to prove Fermat's last theorem. Until 1995, Professor Andrew Wiles of Princeton University in the United States spent 8 years. Working alone, Wiles finally completed the proof in 130 pages.
 Now that Fermat's last theorem has been proved, mathematicians What else can you do with AI? The answer is: formalize its proofs.
Now that Fermat's last theorem has been proved, mathematicians What else can you do with AI? The answer is: formalize its proofs.
Formalization in mathematics usually refers to the use of strict formal languages (such as logic and set theory) to express mathematical objects, structures, Theorems and proofs enable them to be represented, verified and manipulated on computers, thereby ensuring the accuracy and consistency of mathematical content. The development of formal mathematics can be traced back to the late 19th and early 20th centuries, while modern formal mathematics The development of mathematical logic and computer science that began in the 20th century. The main goal of formal mathematics is to establish a formal system, which includes a set of symbols, a set of basic axioms and a set of reasoning rules. Through the application of these rules and axioms,
At the end of last year, Tao Zhexuan et al. Someone once used Lean (an interactive theorem prover and a programming language) to formalize one of their papers. The paper, a proof of a version of the polynomial Freiman-Ruzsa conjecture, was posted on arXiv last November. When writing Lean language code, Tao Zhexuan also used the AI programming assistant Copilot. This incident attracted widespread attention in the mathematics and artificial intelligence communities.
At the time, Kevin Buzzard of Imperial College London, the most important promoter of the Lean technology open source community, said: "Fundamentally, it is obvious that when you digitize something, you can Use it in new ways. We will digitize mathematics, which will make mathematics better."
This is Professor Buzzard, the mathematician who recently claimed to formalize the proof of Fermat's last theorem. The tools are also Lean.
 In a blog, he introduced the background, motivation and specific methods of doing this.
In a blog, he introduced the background, motivation and specific methods of doing this.
The form of Fermat's Last Theorem is very simple and intuitive, but proving it is extremely difficult. This is undoubtedly an excellent demonstration of the profound beauty of mathematics. Over the past few centuries, in order to solve this problem, mathematicians have developed and innovated a large number of mathematical theories, which have applications in fields ranging from cryptography to physics.
Andrew Wiles may have been inspired by FLT, but his work actually led to a breakthrough in the Langlands Project, a series of far-reaching ideas in mathematics that linked number theory, algebraic geometry, and approximation. The theory of group representation is still attracting attention in 2024.
Historically, several other major breakthroughs in algebraic number theory (such as the theory of factorization in number fields and arithmetic in cyclic fields) were motivated at least in part by the desire for a deeper understanding of FLT.
Wiles' work, complemented by his student Richard Taylor, built on a vast foundation of 20th-century mathematics. The basic technique introduced by Wiles - the "modularity lifting theorem" - has been conceptually greatly simplified and widely generalized in the 30 years since the original paper was published. This field is still very active today. Frank Calegari's paper at the 2022 International Congress of Mathematicians, outlining progress since Wiles' breakthrough (see: https://arxiv.org/abs/2109.14145). Kevin Buzzard said that the continued activity in this field was one of his motivations for formalizing the FLT proof.
Formalization of mathematics is the art of converting mathematics on paper into a computer programming language that enables the understanding of theorems and proof concepts. These programming languages, also known as interactive theorem provers (ITPs), have been around for decades. In recent years, however, this area seems to have attracted some attention from the mathematical community. We have witnessed several examples of formalization of research in mathematics, the latest of which is the formalization of the proof of the polynomial Freiman-Ruzsa conjecture by Terence Tao and others. This 2023 breakthrough paper was formalized in Lean in just three weeks. Such success stories might lead onlookers to think that ITPs like Lean are now ready to formalize all modern mathematics.
However, the truth is far from simple. In some areas of mathematics, such as combinatorics, we can see some modern breakthroughs being formalized in real time. However, Buzzard said he regularly attended London number theory seminars and often noticed that Lean's knowledge of modern mathematical definitions was insufficient to formulate the results announced at the seminars, let alone verify their proofs.
In fact, the "lag" of number theory in this aspect was one of Buzzard's main motivations for launching the formalization of contemporary proofs of FLT. By the end of the project, Lean will be able to understand automorphic forms (a special class of functions of complex variables) and representations, Galois representations, latent automorphism, modularity promotion theorems, arithmetic of algebraic varieties, class field theory, arithmetic duals Theorems, Shimura varieties and other concepts used in modern algebraic number theory. In Buzzard's view, with these foundations in place, formalizing what's happening in his own area of expertise will no longer be science fiction.
So, why do this? Buzzard explained, "If we believe some computer scientists, the exponential growth of artificial intelligence will eventually enable computers to help mathematicians in their research. Such work can help computers understand what we are doing in modern mathematical research."
How to carry out the project?
The formalization project of Fermat’s Last Theorem has now been launched. Buzzard shows current progress in a graphic.
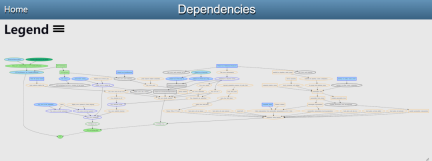
Interested researchers can read details: https://imperialcollegelondon.github.io/FLT/blueprint/dep_graph_document.html
This project is sponsored by EPSRC funding will see Buzzard receive funding for the first five years. During this period, his first goal was to reduce FLT to a statement known to mathematicians in the late 1980s.
Of course, Buzzard had no intention of doing this alone. He said that for some parts of the argument, he understood the basic principles but had never examined the details in detail. Furthermore, Project Langlands also introduced some important things, including GL_2's cyclic basis transformation and Jacquet-Langlands. His understanding of these profound things is not deep enough.
However, this is precisely the advantage of formal projects. Buzzard will be able to articulate the results he needs in Lean and communicate them to others. The beauty of this system is: you don’t have to understand the entire proof of FLT to contribute. The diagram above breaks the proof into many small lemmas, making it very convenient for crowdsourcing. If you can formally prove any of these lemmas, Buzzard would eagerly await your pull request.
Those who want to participate in the project need to know something about Lean. For this, Buzzard recommends the online textbook Mathematics in Lean.
Textbook link: https://leanprover-community.github.io/mathematics_in_lean/
This project will be carried out on the FLT stream of Lean Zulip chat , a powerful research forum where mathematicians and computer scientists can collaborate in real time, easily publishing code and mathematics, using a thread and stream system to effectively support multiple independent conversations at the same time.

Lean Zulip chat link: https://leanprover.zulipchat.com/
Buzzard said he has no idea how long the project will take Premonition, but he's definitely optimistic.
At the same time, formal proof tools like Lean are also constantly iterating. Compared with the original Lean, the latest Lean 4 version has many optimizations, including a faster compiler, improved error handling, and better integration with external tools.
At the end of last year, the open platform LeanDojo team and researchers from the California Institute of Technology also launched Lean Copilot, a collaboration tool designed for large-scale language models to interact with humans, injecting AI into mathematical research. The power of big models.
"I predict that, if used correctly, AI will become a trusted co-author in mathematical research and many other fields by 2026." Tao Zhexuan said in a previous blog.
I hope Terence Tao’s prediction will come true soon.
Related reading:
《Tao Zhexuan’s favored proof assistant Lean uses a large model》
- ##《
Tao Zhexuan’s new project: proving the prime number theorem in Lean, the research blueprint has been completed》
Reference link: https://leanprover.zulipchat.com/#narrow/stream/416277-FLT
https: //mp.weixin.qq.com/s/d9RSkRhlKH5ZMek3yTqe4Q
The above is the detailed content of A relay spanning more than 300 years: Inspired by Terence Teru, mathematicians decided to use AI to formalize the proof of Fermat's Last Theorem.. For more information, please follow other related articles on the PHP Chinese website!
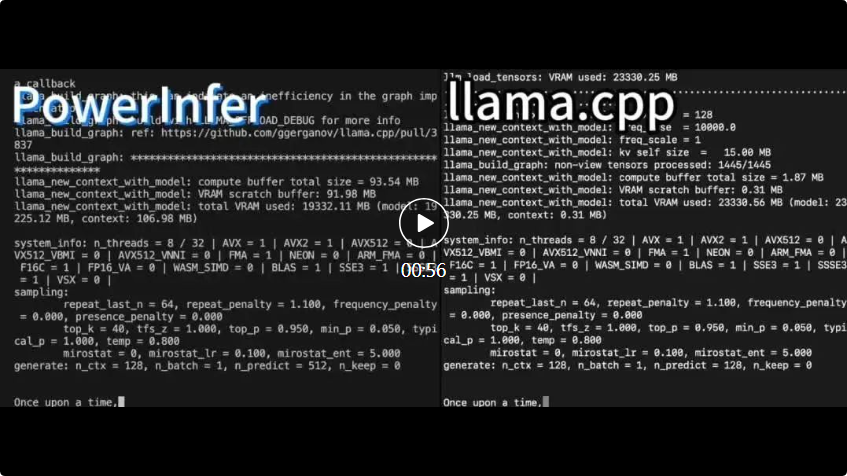 4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PM
4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PMPowerInfer提高了在消费级硬件上运行AI的效率上海交大团队最新推出了超强CPU/GPULLM高速推理引擎PowerInfer。PowerInfer和llama.cpp都在相同的硬件上运行,并充分利用了RTX4090上的VRAM。这个推理引擎速度有多快?在单个NVIDIARTX4090GPU上运行LLM,PowerInfer的平均token生成速率为13.20tokens/s,峰值为29.08tokens/s,仅比顶级服务器A100GPU低18%,可适用于各种LLM。PowerInfer与
 思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM
思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM要让大型语言模型(LLM)充分发挥其能力,有效的prompt设计方案是必不可少的,为此甚至出现了promptengineering(提示工程)这一新兴领域。在各种prompt设计方案中,思维链(CoT)凭借其强大的推理能力吸引了许多研究者和用户的眼球,基于其改进的CoT-SC以及更进一步的思维树(ToT)也收获了大量关注。近日,苏黎世联邦理工学院、Cledar和华沙理工大学的一个研究团队提出了更进一步的想法:思维图(GoT)。让思维从链到树到图,为LLM构建推理过程的能力不断得到提升,研究者也通
 复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM
复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM近期,复旦大学自然语言处理团队(FudanNLP)推出LLM-basedAgents综述论文,全文长达86页,共有600余篇参考文献!作者们从AIAgent的历史出发,全面梳理了基于大型语言模型的智能代理现状,包括:LLM-basedAgent的背景、构成、应用场景、以及备受关注的代理社会。同时,作者们探讨了Agent相关的前瞻开放问题,对于相关领域的未来发展趋势具有重要价值。论文链接:https://arxiv.org/pdf/2309.07864.pdfLLM-basedAgent论文列表:
 大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM
大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM将不同的基模型象征为不同品种的狗,其中相同的「狗形指纹」表明它们源自同一个基模型。大模型的预训练需要耗费大量的计算资源和数据,因此预训练模型的参数成为各大机构重点保护的核心竞争力和资产。然而,与传统软件知识产权保护不同,对预训练模型参数盗用的判断存在以下两个新问题:1)预训练模型的参数,尤其是千亿级别模型的参数,通常不会开源。预训练模型的输出和参数会受到后续处理步骤(如SFT、RLHF、continuepretraining等)的影响,这使得判断一个模型是否基于另一个现有模型微调得来变得困难。无
 FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AM
FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AMFATE2.0全面升级,推动隐私计算联邦学习规模化应用FATE开源平台宣布发布FATE2.0版本,作为全球领先的联邦学习工业级开源框架。此次更新实现了联邦异构系统之间的互联互通,持续增强了隐私计算平台的互联互通能力。这一进展进一步推动了联邦学习与隐私计算规模化应用的发展。FATE2.0以全面互通为设计理念,采用开源方式对应用层、调度、通信、异构计算(算法)四个层面进行改造,实现了系统与系统、系统与算法、算法与算法之间异构互通的能力。FATE2.0的设计兼容了北京金融科技产业联盟的《金融业隐私计算
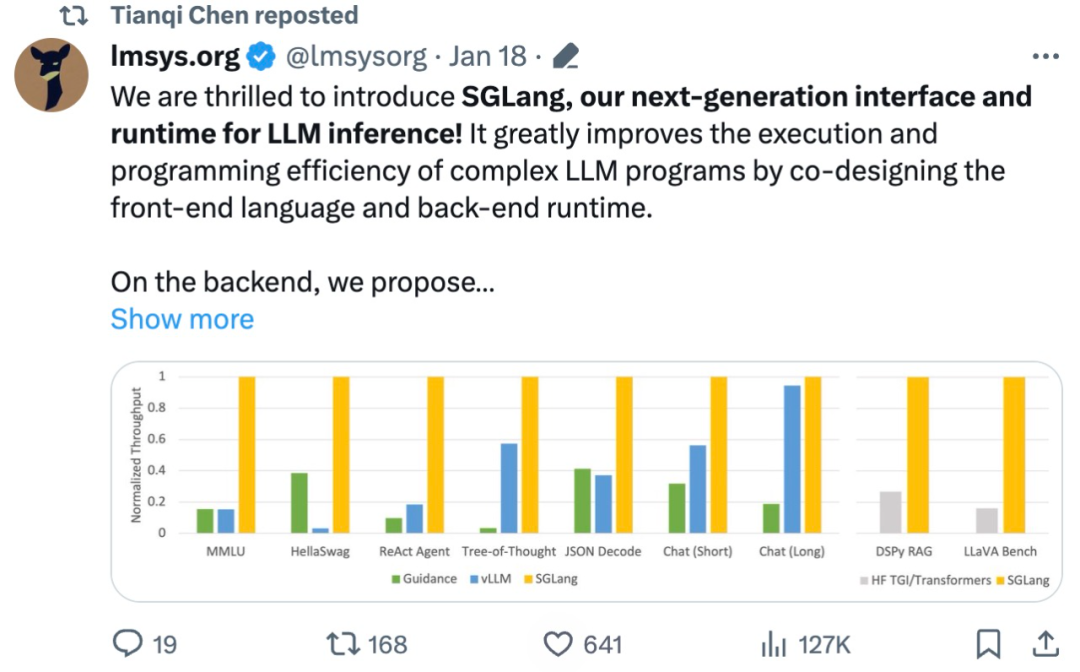 吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM
吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM大型语言模型(LLM)被广泛应用于需要多个链式生成调用、高级提示技术、控制流以及与外部环境交互的复杂任务。尽管如此,目前用于编程和执行这些应用程序的高效系统却存在明显的不足之处。研究人员最近提出了一种新的结构化生成语言(StructuredGenerationLanguage),称为SGLang,旨在改进与LLM的交互性。通过整合后端运行时系统和前端语言的设计,SGLang使得LLM的性能更高、更易控制。这项研究也获得了机器学习领域的知名学者、CMU助理教授陈天奇的转发。总的来说,SGLang的
 220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PM
220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PMIBM再度发力。随着AI系统的飞速发展,其能源需求也在不断增加。训练新系统需要大量的数据集和处理器时间,因此能耗极高。在某些情况下,执行一些训练好的系统,智能手机就能轻松胜任。但是,执行的次数太多,能耗也会增加。幸运的是,有很多方法可以降低后者的能耗。IBM和英特尔已经试验过模仿实际神经元行为设计的处理器。IBM还测试了在相变存储器中执行神经网络计算,以避免重复访问RAM。现在,IBM又推出了另一种方法。该公司的新型NorthPole处理器综合了上述方法的一些理念,并将其与一种非常精简的计算运行
 「花果山名场面」有了高清画质版,NTU提出视频超分框架Upscale-A-VideoJan 11, 2024 pm 07:57 PM
「花果山名场面」有了高清画质版,NTU提出视频超分框架Upscale-A-VideoJan 11, 2024 pm 07:57 PM扩散模型在图像生成方面取得了显著成功,但将其应用于视频超分辨率仍存在挑战。视频超分辨率要求输出保真度和时间一致性,而扩散模型的固有随机性使这变得复杂。因此,有效地将扩散模型应用于视频超分辨率仍是一个具有挑战性的任务。来自南洋理工大学S-Lab的研究团队提出了一种名为Upscale-A-Video的文本指导潜在扩散框架,用于视频超分。该框架通过两个关键机制确保时间一致性。首先,在局部范围内,它将时间层集成到U-Net和VAE-Decoder中,以保持短序列的一致性。其次,在全局范围内,该框架引入了


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

SublimeText3 Chinese version
Chinese version, very easy to use

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

Dreamweaver CS6
Visual web development tools





