How to find the optimal value of a function on the geometric sketchpad

How to find the optimal value of a function in Geometry Sketchpad? PHP editor Xinyi brings you detailed operation steps. This tutorial will guide you step by step to easily implement the optimal function calculation. Through simple operations, you will master how to use its powerful functions to perform mathematical calculations in Geometry Sketchpad.

1. Select [Draw] - [Draw New Function], enter the function expression in the function editor, click OK and the function image will appear.

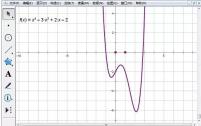
2. Select Custom Tools - Function Tool - Maximum/Minimum Value. Click the expression of function f(x), move the mouse to the function graph, release the mouse when the limit point mark appears, and a maximum or minimum value will be recorded. The figure below shows a minimum coordinate.

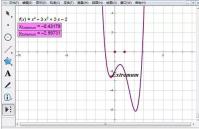
3. Repeat this operation to find the coordinates of the other two extreme points. In this way, all three extreme points have been found.

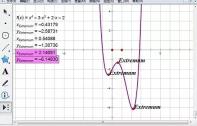
4. Select [Data] - [Calculation], click the function expression, automatically enter f() in the edit box, enter -1 in the brackets, and click Make sure the function value appears on the left. Calculate the function value of the function at x=3 in the same way.

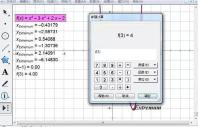
5. Compare the five y values. The conclusion is: the maximum value of the function in the [-1,3] interval is 4 and the minimum value is -6.14830.

The above is the detailed content of How to find the optimal value of a function on the geometric sketchpad. For more information, please follow other related articles on the PHP Chinese website!