 Technology peripherals
Technology peripherals AI
AI Can AI conquer Fermat's last theorem? Mathematician gave up 5 years of his career to turn 100 pages of proof into code
Can AI conquer Fermat's last theorem? Mathematician gave up 5 years of his career to turn 100 pages of proof into codeCan AI conquer Fermat's last theorem? Mathematician gave up 5 years of his career to turn 100 pages of proof into code
Fermat’s Last Theorem is about to be conquered by AI?
And the most meaningful part of the whole thing is that the Fermat’s Last Theorem that AI is about to solve is precisely to prove that AI is useless.
Once upon a time, mathematics belonged to the realm of pure human intelligence; now, this territory is being deciphered and trampled by advanced algorithms.
 Picture
Picture
Fermat’s Last Theorem is a "notorious" puzzle that has been puzzled for centuries. troubles mathematicians.
It was proven in 1993, and now, mathematicians have a great plan: to use computers to reproduce the proof process.
They hope that in this version of the proof, if there are any logical errors, they can be checked by a computer.

Project address: https://github.com/riccardobrasca/flt3
End of March, Mathematician Pietro Monticone said excitedly that he and his colleagues have almost completed the formalization of Fermat's last theorem with exponent 3 in leanprover.
They will port the formal process to Mathlib as soon as possible for use in the FLT project.
 Picture
Picture
The proof process roughly follows Wiles' proof, but with slight changes.
Putting Fermat’s Last Theorem into code with Lean
When April rolls around, mathematician and programmer Kevin Buzzard will release this Plan: Complete the proof of Fermat’s Last Theorem through computer code.
After the project goes online in April, the public blueprint will appear online. At that time, anyone in the Lean community can make their own contribution to the formal proof.
 Picture
Picture
Is it easy to turn a groundbreaking 100-page mathematical proof into computer code?
This is of course thanks to the proof tool Lean, which is highly praised and addicted to use by Terence Tao, which allows users to convert prose-style proofs into rules and logic for testing.
 Picture
Picture
But in any case, this project is not simple and is expected to take many years, and Kevin Buzzard page obtained Project financial support.
 Picture
Picture
Everyone understands that this project is probably one of the most complex computerized demonstrations to date.
 Picture
Picture
Fermat’s Last Theorem
Fermat’s Last Theorem, worthy of Called one of the most exciting mathematical puzzles in history.
The process of proving Fermat’s Last Theorem is directly a history of mathematics.
 Picture
Picture
The familiar Fermat’s Last Theorem was invented by the 17th-century French mathematician Pierre de Fermat. Ma proposed. Unfortunately, he was unable to find proof during his lifetime.
В результате эта проблема, возникшая более 300 лет назад, на протяжении трех столетий бросала непосредственный вызов человечеству, много раз потрясала мир, истощила энергию многих самых выдающихся умов человечества и оставила миллионы любителей одержим этим.
 ##Picture
##Picture
Эта теорема утверждает, что не существует трех натуральных чисел a, b, c, удовлетворяющих уравнению (a^ n b ^n = c^n), где n — любое целое число, большее 2.
Трудность этого доказательства состоит в том, что математикам трудно найти отрицательный случай: как мы можем гарантировать, что не должно существовать такого бесконечного целого числа n, которое могло бы удовлетворять этому уравнению?
 Picture
Picture
 ## К счастью, для современных математиков преобразование понятия бесконечности в логику не является чем-то новым. Все кончено.
## К счастью, для современных математиков преобразование понятия бесконечности в логику не является чем-то новым. Все кончено.
В более простых доказательствах мы можем полагаться на индукцию -
Как только определенная логика справедлива для определенного числа (например, 8 ), тогда это также верно для каждого последующего числа (например, 9, 10, 11 и т. д.) до бесконечности.
 Picture
Picture
Однако Великая теорема Ферма была камнем преткновения в мире математики на протяжении сотен лет.
До 1993 года британский математик Эндрю Уайлс разгадал эту загадку с помощью 100-страничного письменного доказательства.
Picture
#Почему компьютеры не могут доказать Великую теорему Ферма?Промышленность считает, что есть три причины:
#1. Компьютеры не могут вывести бесконечное количество видов
2. Компьютеры не могут доказать логическую правильность
#3. Компьютеры могут совершать мимолетные ошибки
К счастью, есть вспомогательное доказательство Lean
Математическое доказательство на 100 страниц не так уж и просто для обычных студентов-математиков или математиков.Легко контролировать.
 К счастью, мы больше не можем полагаться на традиционные методы доказательства и можем обратиться к таким инструментам, как Lean.
К счастью, мы больше не можем полагаться на традиционные методы доказательства и можем обратиться к таким инструментам, как Lean.
Это инструмент программирования на основе C, предназначенный для написания и проверки индукционных доказательств.
Многие из сегодняшних так называемых «искусственных интеллектов» представляют собой не что иное, как искусно составленные слова, имитирующие человеческий язык. Но компьютерные доказательства, такие как Lean, более глубоко интегрируют человеческое мышление и расширенные возможности компьютера.
Изображение
Инструменты бережливого программирования, поступление в класс бакалавриата
at Imperial Лондон Кевин Баззард, преподающий математику в Политехническом институте, потратил несколько лет на разработку инструментов поддержки с использованием Lean для всей учебной программы бакалавриата по математике в колледже.
С помощью этих инструментов учащиеся могут разбить обсуждаемый в классе материал на логические и математические этапы.
 Это похоже на Розеттский камень математических доказательств.
Это похоже на Розеттский камень математических доказательств.
Кларисса Литтлер, которая также является учителем математики, полностью согласна с философией Кевина Баззарда.
### Она преподает дискретную математику в Портлендском муниципальном колледже. В течение последних двух семестров она использовала на уроках дискретной математики «Классическую вводную игру по бережливому производству», разработанную Кевином Баззардом. ###############Изображение############Адрес: https://adam.math.hhu.de/######Она будет использовать «Игру с натуральными числами», чтобы помочь учащимся ознакомиться с идеей математической индукции, а с помощью «Игры по теории множеств» позволит им привыкнуть к рассуждениям о множествах.
 ##Картинка
##Картинка
##В этом процессе студенты узнали о «написании доказательств в строгом соответствии с логическими правилами» и «использовании популярных язык. Разрыв в понимании между «объяснением истины вещей» постепенно будет преодолен.
Литтлер подчеркнул, что основная цель курса - дать возможность студентам со слабыми знаниями в математике мыслить более свободно, как математики, а также лучше понимать доказательства, доказательства и способы. чтобы продемонстрировать истину.
Этот переход от формальной логики к спискам правил и прозе является ключом к разбиению проектов на взаимодействующие фрагменты кода.
 Картинка
Картинка
И это особенно важно на стыке программирования и чистой математики, а именно такие инструменты, как Lean A место, где можно сиять.
Баззард заявил, что надеется преобразовать сложные математические идеи, вдохновленные Великой теоремой Ферма, в программируемую форму.
На протяжении веков было создано множество ценных новых разделов математики, чтобы доказать эту теорему, которая, по мнению Баззарда, «не имеет практического значения».
Да, по мнению Баззарда, последняя теорема Ферма бессмысленна и не имеет применения в реальном мире.Однако из-за этой «пресловутой» проблемы некоторые практичные люди генерируют много отличные новые идеи.
Теперь преобразование 100-страничного доказательства Уайлса в формальный язык и правила, понятные компьютерам, как ожидается, откроет дверь к компьютерным доказательствам для нового поколения математиков.
 Picture
Picture
Этот инструмент преобразования также может помочь программистам.
Литтлер сказал, что в этой области всегда стоит попробовать амбициозные проекты, потому что мы все можем извлечь пользу из извлеченных уроков и написанных библиотек.
Хотя интерактивное доказательство теорем все еще является относительно новой областью, сообщество Lean проделало много превосходной работы.
##Кевин Баззард: евангелист бережливого производства
Кевин Марк Баззард, родившийся в 1968 году, обладает глубокими знаниями в области арифметической геометрии и программ Ленглендса. Достижения.В настоящее время он профессор чистой математики в Имперском колледже Лондона и «евангелист» инструмента искусственного интеллекта Lean.
Во время учебы в Королевской гимназии Кевин Баззард участвовал в Международной математической олимпиаде, завоевав бронзовую медаль в 1986 году и золотую медаль с высшими баллами в 1987 году.
Picture
Под руководством Ричарда Тейлора в 1995 году была завершена его докторская диссертация «Уровни модульных представлений», посвященная сложной области математики.
##Фото
 В 1998 году начал работать преподавателем в Имперском колледже Лондона. В 2002 году получил звание старшего преподавателя. и в 2004 году получил звание старшего преподавателя. Назначен профессором.
В 1998 году начал работать преподавателем в Имперском колледже Лондона. В 2002 году получил звание старшего преподавателя. и в 2004 году получил звание старшего преподавателя. Назначен профессором.
Он также проводил выездные исследования в Гарвардском университете (октябрь-декабрь 2002 г.) и ряде других известных учреждений.
За выдающийся вклад в область теории чисел он получил премию Уайтхеда в 2002 году и премию Бервика в 2008 году.
В 2017 году Buzzard запустил проект и блог о средстве доказательства теорем бережливого производства, посвященный пропаганде использования инструментов компьютерного доказательства в математических исследованиях.
Он также руководил музыкантом Дэном Снайтом (сценический псевдоним Карибу) в его докторской диссертации по математике, посвященной изучению суперконвергентных символов модуля Зигеля, за что Снэйт получил докторскую степень в Имперском колледже Лондона.
В октябре 2023 года Кевин Баззард заявил в социальных сетях, что получил финансирование на исследования и начал использовать Lean для доказательства Великой теоремы Ферма.
 Picture
Picture
«Десять лет назад это заняло бы бесконечное количество времени», - сказал Баззард. Он отложит свои преподавательские обязанности на пять лет, чтобы завершить проект.
Стоит ли откладывать собственные дела?
По мнению его коллеги Криса Уильямса из Ноттингемского университета в Великобритании, такого рода проекты могут иметь неожиданные преимущества и далеко идущие последствия.
«Думаю, маловероятно, что он формально формализует все доказательство в течение ближайших пяти лет, иначе это было бы потрясающе. Однако многих инструментов теории чисел и арифметической геометрии нигде нет». найти сегодня Не здесь, поэтому я ожидаю, что любой существенный прогресс в будущем будет очень полезен."
Важно для математических исследований
Этот проект также раскрывает более глубокую ценность.
С непрерывным развитием вычислительных средств границы между разными разделами математики и даже между разными дисциплинами становятся все более размытыми, в результате чего возникают некоторые задачи, проверить которые практически невозможно. Доказательство появилось.
Например, японский математик Мотидзуки Синити из Киотского университета написал доказательство на 500 страниц. На его публикацию ушло несколько лет, потому что оно было очень сложным, отчасти потому, что люди не знали Что с этим делать.
С этого момента мы можем обнаружить, что границы математики становятся все более размытыми.
Это относится не к правдивости или логической двусмысленности, а к диапазону различных идей, которые могут быть включены в доказательство.
Lean позволяет математикам преобразовывать свои идеи в код, облегчая понимание коллегами. Глядя на прецеденты, зафиксированные предшественниками, будущие математики смогут продолжать на этой основе свои собственные исследования.
Баззард сказал, что особенностью математического письма в Lean является то, что вы можете оставить после себя точно сформулированные, но недоказанные результаты, а другие смогут решить их позже.
Lean сам по себе облегчает такой рабочий процесс.
 ##Picture
##Picture
Другими словами, Великая теорема Ферма готовится к решению посредством «краудсорсинга» — особенно если программирование продолжится и дальше Оставшиеся годы работы Баззарда.
Завершение математического доказательства требует усилий всего сообщества.
Возможно, в будущем у нас появится платформа, подобная Genius.com, для обмена и интерпретации математических доказательств.
Ссылка:
The above is the detailed content of Can AI conquer Fermat's last theorem? Mathematician gave up 5 years of his career to turn 100 pages of proof into code. For more information, please follow other related articles on the PHP Chinese website!
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s
 New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AM
New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AMGoogle's Gemini Advanced: New Subscription Tiers on the Horizon Currently, accessing Gemini Advanced requires a $19.99/month Google One AI Premium plan. However, an Android Authority report hints at upcoming changes. Code within the latest Google P
 How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AM
How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AMDespite the hype surrounding advanced AI capabilities, a significant challenge lurks within enterprise AI deployments: data processing bottlenecks. While CEOs celebrate AI advancements, engineers grapple with slow query times, overloaded pipelines, a
 MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AM
MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AMHandling documents is no longer just about opening files in your AI projects, it’s about transforming chaos into clarity. Docs such as PDFs, PowerPoints, and Word flood our workflows in every shape and size. Retrieving structured
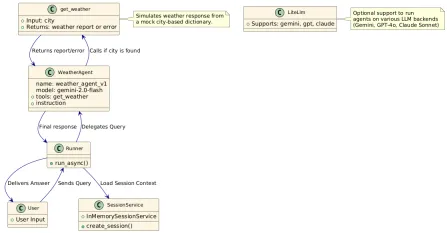 How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AM
How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AMHarness the power of Google's Agent Development Kit (ADK) to create intelligent agents with real-world capabilities! This tutorial guides you through building conversational agents using ADK, supporting various language models like Gemini and GPT. W
 Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AM
Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AMsummary: Small Language Model (SLM) is designed for efficiency. They are better than the Large Language Model (LLM) in resource-deficient, real-time and privacy-sensitive environments. Best for focus-based tasks, especially where domain specificity, controllability, and interpretability are more important than general knowledge or creativity. SLMs are not a replacement for LLMs, but they are ideal when precision, speed and cost-effectiveness are critical. Technology helps us achieve more with fewer resources. It has always been a promoter, not a driver. From the steam engine era to the Internet bubble era, the power of technology lies in the extent to which it helps us solve problems. Artificial intelligence (AI) and more recently generative AI are no exception
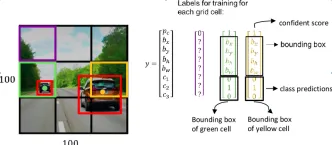 How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AM
How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AMHarness the Power of Google Gemini for Computer Vision: A Comprehensive Guide Google Gemini, a leading AI chatbot, extends its capabilities beyond conversation to encompass powerful computer vision functionalities. This guide details how to utilize
 Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AMThe AI landscape of 2025 is electrifying with the arrival of Google's Gemini 2.0 Flash and OpenAI's o4-mini. These cutting-edge models, launched weeks apart, boast comparable advanced features and impressive benchmark scores. This in-depth compariso


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Atom editor mac version download
The most popular open source editor

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

Dreamweaver CS6
Visual web development tools

SublimeText3 Chinese version
Chinese version, very easy to use

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software






