 Technology peripherals
Technology peripherals AI
AI AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence TaoAI は確かに数学を変えています。
最近、この問題に細心の注意を払っている陶哲軒氏が、「米国数学協会会報」の最新号を送ってくれました。
「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。
著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピュータ科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っています。

AI の世界は劇的に変化しました。ご存知のとおり、これらの記事の多くは 1 年前に投稿されたものですが、今年中に AI は次のような変化を遂げました。多くの重要な変更。
しかし、それにもかかわらず、これらの記事は依然として金に満ちており、テレンス・タオさえ叫ばせました:この分野の進歩は速すぎます!私の未公開記事が冗長であるように見えます。
AI ツールが数学の分野を驚くべき速度で進歩させていることは誰も否定できません。
人工知能は、純粋数学を含む科学分野における情報の収集と処理の方法に革命をもたらすのでしょうか?それは数学のやり方を変えるだろうか?
数学者の意見は分かれています。研究における機械学習の普及が目前に迫っていると信じている人もいれば、懐疑的な人もいます。1960 年代とその後の過度の楽観主義を振り返ると、 AIウィンター」。
しかし、数学研究の実践では劇的な変化が起こる可能性が非常に高いです。さて、数学者はこれらの変化が引き起こす問題を検討する時が来ました。
嵐が近づいていることは疑いの余地がありません。
それでは、機械は数学を変えるのでしょうか?
数学的研究に対する数学的自動化の影響
この論文では、フィールズ賞受賞者のアクシャイ・ヴェンカテシュが数学的研究に対する自動化の影響について調査します。

論文アドレス: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024- 01834-5/S0273-0979-2024-01834-5.pdf

この論文では、Akshay Venkatesh が興味深いアイデアを提案しました 実験 -
2017 年、DeepMind の Alphazero は、チェスと囲碁を一晩で学習し、人間を超えました。
10 年後、「Alephzero」 ( と表記) も同じ形式の数学を行ったらどうなるでしょうか?
と表記) も同じ形式の数学を行ったらどうなるでしょうか?
この記事の「数学」は「純粋な数学的研究」を指します。
私たちの出発点は、「Alephzero」が高校と大学の数学を独学で学び、SpringerVerlag の数学大学院シリーズのすべての演習を完了したと仮定することです。翌朝、数学者がそれを発表し、子供たちがそれをダウンロードし、私たちのコンピューティング リソースで実行しました。
これは明らかに非現実的なため、確かに思考実験です。視野を今後 10 年または 20 年に限定することで、この思考に伴う可能性から距離を置くことができます。これを技術の進歩の結果として起こる社会的変化として考えることで、より極端なタイプの機械知能について考えることを避けることができます。そこでは、アレフゼロを生きた協力者ではなく動力ツールとしてモデル化します。
私たちは次のように自分を慰めることができます。実際、この前提は私たちからかけ離れているので、考える必要はありません。しかし、ほんのわずかな可能性さえ許せば、これは20年後に起こる可能性があります。
数学者と問題ネットワークのベイズ相互作用を通じて、私たちの価値メカニズムの一部を示す非常に大まかなモデルを提供します。ここで、「Alephzero」がこのネットワークにどのような影響を与え、結果を変えるかを検討します。
これまで見てきたように、困難の認識は、価値を構築する方法の重要な部分です。
特定の状況に関係なく、「Alephzero」は私たちの問題解決能力を変え、それによって問題の難しさに対する私たちの認識を変えます。
数学的プロセスの中で最も速く加速できる部分は、知覚される困難さを最も大きく軽減し、上記のモデルによれば、状態は最も大きな軽減を受けることになります。同様のパターンが自動化の多くのインスタンスで発生します。
最後に、「Alephzero」は数学における興味深い問題の範囲を大幅に拡張します。それはプロの数学者と他の人々との間の競争の場を平等にするでしょう。
機械が数学をより集約化する方法

論文アドレス: https://www.ams .org/journals/bull/2024-61-02/S0273-0979-2024-01827-8/S0273-0979-2024-01827-8.pdf

## 数学者の鄭楽軍氏は、テクノロジーによって数学の勉強方法が変わったため、テクノロジーの進歩に直面して人間の数学者を不要にするのではなく、このテクノロジーを利用して数学をより「収束」させることができると信じています。
「数学を行う」とはどういうことかを考える中で、彼女は数学テクノロジーの次の側面を検討しました:教育と学習、質問、コラボレーション、コミュニケーション、研究行為。
これは厳密な分析ではなく、数学者としての彼女の経験に基づいた賢明な考察です。
Zheng Lejun 氏は、コンピューター支援の校正チェッカーや証明ジェネレーターさえもいくつか存在しますが、テクノロジーは数学研究の最も奥深く、創造的で人道的な側面に実際には侵入していないと考えています。 。
ディープクリエイティブな部分では、最初にアイデアを考えることが含まれます。定義のアイデア、証明のアイデア、数学のさまざまな部分を接続するアイデア、物事を表現する新しい方法のアイデア、アイデアなどです。記号や用語、図式的な推論のアイデア、視覚的表現のアイデア。
機械に数学的研究をさせるには、それを行うように指示する方法を見つけなければなりません。自分で行う方法がわからない場合は、私たちにとってその方法を教えるのは難しいです。
機械はある程度の証明チェックを行うことができますが、密かに数学者は完全に厳密な証明を書くことはできないことを知っています。私たちは論理に基づいて議論し、論理に裏付けられています。私たちの同僚が記入できると思われる手順。
これらのステップのサイズは定義されていないため、マシンにそれを実行するように指示するのは困難です。
数学の学生なら誰でも知っているように、証明を生成することは、単に証明をチェックすることとはまったく異なるスキルです。自分で新しい証拠を考え出すよりも、他の人の証拠に従う方がはるかに簡単です。これは、数学研究においてコンピュータが人間の数学者を決して超えることができないということではありません。
彼女の意見では、コンピューターが人間の数学者よりも優れているのは、
コンピューターは、検索によってすべての可能なアクションを検索する能力が優れているということです。考えられるすべての論理的帰結が現在わかっているので、彼らは新しい数学を考え出すことを試みることができます。
これには、想像力の飛躍、推測、直感が必要ですが、コンピューターでこれを行うには何が十分でしょうか?そのアイデアはとても興味深いですね。
#コンピュータは論理的推論に役立つのか

論文アドレス: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01833-3/S0273-0979-2024-01833-3.pdf

コンピューターは数学研究の方法に革命をもたらし、複雑な計算を簡単に実行できるようにしました。
しかし次に、彼らは私たちの論理的推論のアシスタントになるでしょうか?彼らはいつか独立して推論できるでしょうか?
この記事では、ニューラル ネットワーク、コンピューター定理証明器、大規模言語モデルにおける最近の重要な開発について説明します。
#正式なツールは数学的研究の向上にどのように役立つか
紙のアドレス: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01832-1/S0273-0979-2024-01832-1.pdf

20 世紀初頭以来、私たちは数学的な定義と証明が厳密な構文と規則を備えた正式なシステムを通じて表現できることを理解してきました。
これに基づいて、コンピューター証明アシスタントの開発により、数学的知識をデジタル形式でエンコードできるようになります。
この記事では、この種のテクノロジーとその関連ツールが、より優れた数学的研究にどのように役立つかを検討します。
#定理証明器を使用して数学研究における複雑な問題を単純化する

##論文アドレス: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01831-X/S0273-0979-2024-01831-X.pdf
この記事では、インタラクティブな定理証明器を使用して、抽象的な境界を設定することで数学研究における複雑な問題を単純化する方法を検討します。
奇妙な新しい世界: LLM により、数学者はより自然な言語で証明助手とコミュニケーションできるようになります


大規模言語モデル (LLM) には、この障壁を打ち破る可能性があり、数学者がより自然な言語で証明アシスタントとコミュニケーションできるようになります。これにより、直観力が養われるだけでなく、推論が正しいことも保証されます。
深層学習ツールを使用した純粋な数学的研究

 #この記事は個人的な経験であり、純粋な数学者が研究で深層学習ツールを使用しようとするときに期待することを非公式に共有するものです。
#この記事は個人的な経験であり、純粋な数学者が研究で深層学習ツールを使用しようとするときに期待することを非公式に共有するものです。
AI は数学的研究を行うことができますか?
Paper address: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01828-X/S0273- 0979-2024-01828-X.pdf This article explores the current performance of AI technology in solving word problems that combine basic mathematics and common sense reasoning. Capabilities and limitations. The author reviews three methods developed using AI natural language technology: directly giving answers, generating computer programs that solve problems, and generating formalizations that can be used by automated theorem testers Expression. The author believes that the importance of these limitations in the development of AI technology for pure mathematical research has not yet been clearly defined, but they are extremely critical in mathematical applications and in developing computers that can understand human-written software. Mathematics content is also important during the program. Paper address: https://www. ams.org/journals/bull/2024-61-02/S0273-0979-2024-01826-6/S0273-0979-2024-01826-6.pdf In this article, the author explores the nature of proof and its evolution in the machine age, analyzing it by comparing the values in traditional verification and computer verification. The method ultimately proposed in the article may allow computers to prove successful strategies borrowed from human experience. Paper address: https://www .ams.org/journals/bull/2024-61-02/S0273-0979-2024-01825-4/S0273-0979-2024-01825-4.pdf In the paper, the authors harshly criticize colleagues for their lack of thinking, especially when considering the mechanized future of mathematics, and for ignoring important debates about technology and artificial intelligence at a wider level in society. Paper address: https://www .ams.org/journals/bull/2024-61-02/S0273-0979-2024-01819-9/S0273-0979-2024-01819-9.pdf Continued fractions It has a long history in number theory, especially in the field of Diophantine approximation. This article aims to outline the core results of p-adic continued fraction theory, which is a continued fraction defined on the p-adic number field Qp. The content will start from basic concepts to introduce the latest progress and open issues currently faced. By the way, Tao Zhexuan also made use of the "Machine assisted proof" of the paper he wrote before. Paper address: https://terrytao.files.wordpress.com/2024/03/machine-assisted-proof-notices.pdf In this paper, Tao Zhexuan said that with the help of LLM's ability to process natural language input, they are likely to become a user-friendly platform, allowing mathematicians without specific software knowledge to use advanced tools. Today, he and many scientists are accustomed to using these models to generate simple code in various languages, including symbolic algebra packages, or to create complex diagrams and images. Currently, formal proof verification (formal proof verification) relies heavily on human effort, which makes it impractical to fully formalize a large number of current research papers in real time. In the field of partial differential equations, it is often necessary to go through multiple pages of calculations to estimate integral expressions involving one or more unknown functions (such as the solution of a PDE). This involves using the bounds of these functions in different function space norms (such as Sobolev space norm), combined with standard inequalities (such as Hölder inequality and Sobolev inequality), and such as Differential identities in integral or integral notation. Although this type of calculation is a routine operation, it may contain various degrees of errors (such as sign errors). For reviewers, carefully checking these calculations is tedious and time-consuming. , and the calculations themselves hardly provide deeper mathematical understanding or insight other than the final estimate being correct. It is conceivable that in the future tools may be developed to establish mathematical estimates in an automatic or semi-automatic manner, and replace the current lengthy and uninspiring estimation proofs with a pointing formal proof Link to the certificate. Going a step further, we might be able to expect that, based on an initial set of assumptions and methods, a future AI tool will be able to come up with the best estimate it can, without having to do a paper first Pen calculations were made to predict what this estimate might be. At present, it is estimated that the possible state space is too complex to be explored automatically; but with the development of technology, the possibility of realizing such automated exploration is not out of reach. Once achieved, we will be able to conduct mathematical exploration at a scale that currently seems unfeasible. Let’s take partial differential equations as an example. Current research usually only studies one or two equations at a time; but in the future, we may be able to study hundreds of equations at the same time. For example, first develop a complete argument for an equation, and then let the AI tool adapt these arguments to a large number of related equation families, if necessary, when the expansion of the argument presents unconventional situations , the AI will ask the author questions. Now, in other areas of mathematics, such as graph theory, the first signs of such large-scale mathematical exploration are beginning to appear. However, these current preliminary attempts are difficult to promote on a large scale because they rely on AI models with extremely high computational costs or require a large amount of expert-level human participation and supervision. However, Terence Tao believes that in the near future, we will witness the birth of more innovative machine-assisted mathematical methods. 

What is proof in the machine age


Automation allows mathematicians to reflect on their own value


Continued fractions in p-adic number field

Tao Zhexuan posted: Machine assisted proof


The above is the detailed content of AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao. For more information, please follow other related articles on the PHP Chinese website!
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s
 New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AM
New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AMGoogle's Gemini Advanced: New Subscription Tiers on the Horizon Currently, accessing Gemini Advanced requires a $19.99/month Google One AI Premium plan. However, an Android Authority report hints at upcoming changes. Code within the latest Google P
 How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AM
How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AMDespite the hype surrounding advanced AI capabilities, a significant challenge lurks within enterprise AI deployments: data processing bottlenecks. While CEOs celebrate AI advancements, engineers grapple with slow query times, overloaded pipelines, a
 MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AM
MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AMHandling documents is no longer just about opening files in your AI projects, it’s about transforming chaos into clarity. Docs such as PDFs, PowerPoints, and Word flood our workflows in every shape and size. Retrieving structured
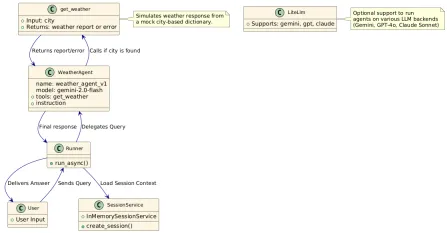 How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AM
How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AMHarness the power of Google's Agent Development Kit (ADK) to create intelligent agents with real-world capabilities! This tutorial guides you through building conversational agents using ADK, supporting various language models like Gemini and GPT. W
 Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AM
Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AMsummary: Small Language Model (SLM) is designed for efficiency. They are better than the Large Language Model (LLM) in resource-deficient, real-time and privacy-sensitive environments. Best for focus-based tasks, especially where domain specificity, controllability, and interpretability are more important than general knowledge or creativity. SLMs are not a replacement for LLMs, but they are ideal when precision, speed and cost-effectiveness are critical. Technology helps us achieve more with fewer resources. It has always been a promoter, not a driver. From the steam engine era to the Internet bubble era, the power of technology lies in the extent to which it helps us solve problems. Artificial intelligence (AI) and more recently generative AI are no exception
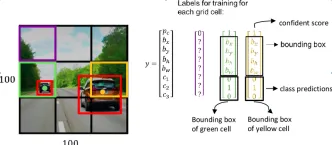 How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AM
How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AMHarness the Power of Google Gemini for Computer Vision: A Comprehensive Guide Google Gemini, a leading AI chatbot, extends its capabilities beyond conversation to encompass powerful computer vision functionalities. This guide details how to utilize
 Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AMThe AI landscape of 2025 is electrifying with the arrival of Google's Gemini 2.0 Flash and OpenAI's o4-mini. These cutting-edge models, launched weeks apart, boast comparable advanced features and impressive benchmark scores. This in-depth compariso


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

Dreamweaver Mac version
Visual web development tools

Notepad++7.3.1
Easy-to-use and free code editor

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool






