 Technology peripherals
Technology peripherals AI
AI The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.
The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.

Editor | XS
Nature published two important research results in November 2023: protein synthesis technology Chroma and crystal material design method GNoME. Both studies adopted graph neural networks as a tool for processing scientific data.
In fact, graph neural networks, especially geometric graph neural networks, have always been an important tool for scientific intelligence (AI for Science) research. This is because physical systems such as particles, molecules, proteins, and crystals in the scientific field can be modeled into a special data structure—geometric graphs.
Different from general topological diagrams, in order to better describe the physical system, geometric diagrams add indispensable spatial information and need to meet the physical symmetry of translation, rotation and flipping. In view of the superiority of geometric graph neural networks for modeling physical systems, various methods have emerged in recent years, and the number of papers continues to grow.
Recently, Renmin University of China and Hillhouse, together with Tencent AI Lab, Tsinghua University, Stanford and other institutions, released a review paper: "A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications". Based on a brief introduction to theoretical knowledge such as group theory and symmetry, this review systematically reviews the relevant geometric graph neural network literature from data structures and models to numerous scientific applications.

Paper link: https://arxiv.org/abs/2403.00485
GitHub link: https:/ /github.com/RUC-GLAD/GGNN4Science
In this review, the author investigated more than 300 references, summarized 3 different geometric graph neural network models, and introduced particle-oriented A total of 23 related methods for different tasks on various scientific data such as molecules, proteins, etc., and more than 50 related evaluation data sets have been collected. Finally, the review looks forward to future research directions, including geometric graph basic models, combination with large language models, etc.
The following is a brief introduction to each chapter.
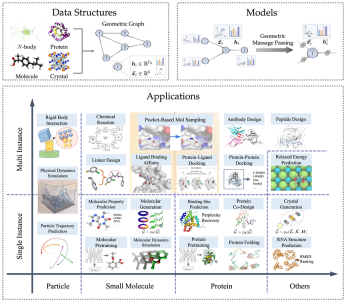
Geometric graph data structure
Geometric graph consists of adjacency matrix, node characteristics, node geometric information (such as coordinates). In Euclidean space, geometric figures usually show physical symmetries of translation, rotation and reflection. Groups are generally used to describe these transformations, including Euclidean group, translation group, orthogonal group, permutation group, etc. Intuitively, it can be understood as a combination of four operations: displacement, translation, rotation, and flipping in a certain order.
For many AI for Science fields, geometric graphs are a powerful and versatile representation method that can be used to represent many physical systems, including small molecules, proteins, crystals, physical point clouds, etc.
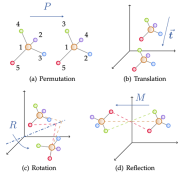
Geometric graph neural network model
According to the requirements for symmetry of the solution goals in actual problems, this article uses geometric graph neural network Networks are divided into three categories: invariant (invariant) model, equivariant (equivariant) model, and Geometric Graph Transformer inspired by the Transformer architecture. The equivariant model is subdivided into scalarization-based model (Scalarization-Based Model) and based on High-Degree Steerable Model of spherical harmonization. According to the above rules, the article collects and categorizes well-known geometric graph neural network models in recent years.

Here we briefly introduce the invariant model (SchNet[1]), the scalarization method model (EGNN[2]), and the high-order scalable model through the representative work of each branch. The correlation and difference between manipulation models (TFN[3]). It can be found that all three use message passing mechanisms, but the latter two, which are equivariant models, introduce an additional geometric message passing.
The invariant model mainly uses the characteristics of the node itself (such as atom type, mass, charge, etc.) and the invariant characteristics between atoms (such as distance, angle [4], dihedral angle [5]), etc. Message computation is performed and subsequently propagated.
On top of this, the scalarization method additionally introduces geometric information through the coordinate difference between nodes, and uses the invariant information as the weight of the geometric information for linear combination, realizing the introduction of equivariance.
High-order controllable models use high-order Spherical Harmonics and Wigner-D matrices to represent the geometric information of the system. This method uses the Clebsch–Gordan coefficient in quantum mechanics to control the order of irreducible representation. numbers, thereby realizing the geometric message passing process.

Geometric graph neural network has greatly improved the accuracy through the symmetry guaranteed by this type of design, and it also shines in the generation task.
The following figure is the results of the three tasks of molecular property prediction, protein-ligand docking and antibody design (generation) using the geometric graph neural network and the traditional model on the three data sets of QM9, PDBBind and SabDab. The advantages of geometric graph neural networks can be clearly seen.

Scientific Applications
In terms of scientific applications, the review covers physics (particles), biochemistry (small molecules, proteins) As well as other application scenarios such as crystals, starting from the task definition and the type of symmetry required to ensure, the commonly used data sets in each task and the classic model design ideas in this type of tasks are introduced.

The above table shows common tasks and classic models in various fields. Among them, according to single instance and multiple instances (such as chemical reactions, which require the participation of multiple molecules), the article is separate Three areas are distinguished: small molecule-small molecule, small molecule-protein, and protein-protein.
In order to better facilitate model design and experiment development in the field, the article counts common data sets and benchmarks (benchmarks) for two types of tasks based on single instance and multiple instances, and records samples of different data sets. Quantity and type of tasks.
The following table summarizes common single-instance task data sets.

The following table summarizes common multi-instance task data sets.

Future Outlook
The article makes a preliminary outlook on several aspects, hoping to serve as a starting point:
1. Geometric graph basic model
The advantages of using a unified basic model in various tasks and fields have been fully reflected in the significant progress of the GPT series models. How to carry out reasonable design in task space, data space and model space, so as to introduce this idea into the design of geometric graph neural network, is still an interesting open problem.
2. Efficient cycle of model training and real-world experimental validation
Acquisition of scientific data is expensive and time-consuming, and only evaluation on independent data sets Models cannot directly reflect feedback from the real world. The importance of how to achieve efficient model-reality iterative experimental paradigms similar to GNoME (which integrates an end-to-end pipeline including graph network training, density functional theory calculations and automated laboratories for materials discovery and synthesis) will It will increase day by day.
3. Integration with Large Language Models (LLMs)
Large Language Models (LLMs) have been widely proven to have rich knowledge, covering various fields. Although there have been some works utilizing LLMs for certain tasks such as molecular property prediction and drug design, they only operate on primitives or molecular graphs. How to organically combine them with geometric graph neural networks so that they can process 3D structural information and perform prediction or generation on 3D structures is still quite challenging.
4. Relaxation of equivariance constraints
There is no doubt that equivariance is crucial to enhance data efficiency and model generalization ability, but it is worth noting that , too strong equivariance constraints can sometimes be too restrictive of the model, potentially harming its performance. Therefore, how to balance the equivariance and adaptability of the designed model is a very interesting question. Exploration in this area can not only enrich our understanding of model behavior, but also pave the way for the development of more robust and general solutions with wider applicability.
References
[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al. Schnet: A continuous-filter convolutional neural network for modeling quantum interactions[ J]. Advances in neural information processing systems, 2017, 30.
[2] Satorras V G, Hoogeboom E, Welling M. E (n) equivariant graph neural networks[C]//International conference on machine learning. PMLR, 2021: 9323-9332.
[3] Thomas N, Smidt T, Kearnes S, et al. Tensor field networks: Rotation-and translation-equivariant neural networks for 3d point clouds[J]. arXiv preprint arXiv:1802.08219, 2018.
[4] Gasteiger J, Groß J, Günnemann S. Directional Message Passing for Molecular Graphs[C]//International Conference on Learning Representations. 2019.
[5] Gasteiger J, Becker F, Günnemann S. Gemnet: Universal directional graph neural networks for molecules[J]. Advances in Neural Information Processing Systems, 2021, 34: 6790-6802.
[6] Merchant A, Batzner S, Schoenholz S S, et al. Scaling deep learning for materials discovery[J]. Nature, 2023, 624(7990): 80-85.
The above is the detailed content of The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.. For more information, please follow other related articles on the PHP Chinese website!
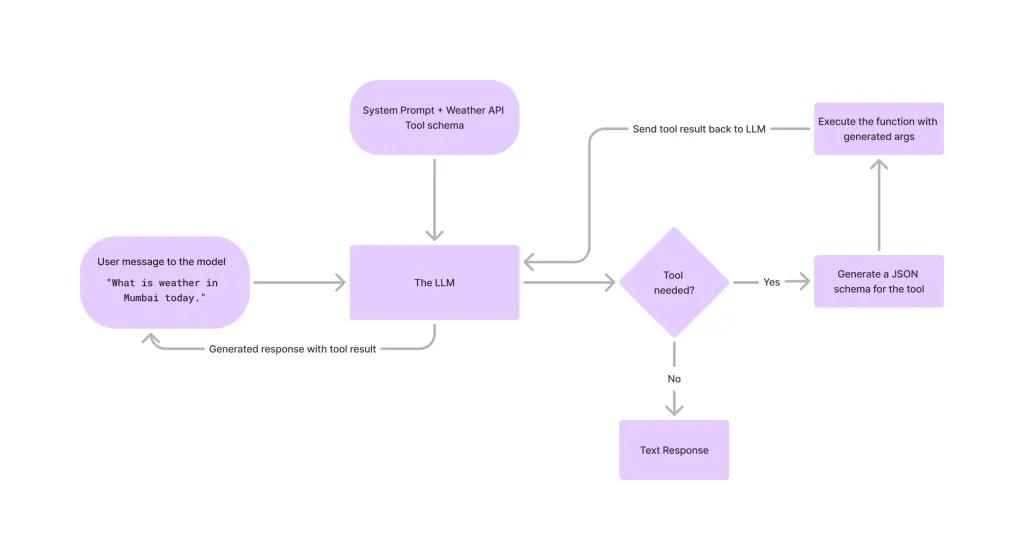 Tool Calling in LLMsApr 14, 2025 am 11:28 AM
Tool Calling in LLMsApr 14, 2025 am 11:28 AMLarge language models (LLMs) have surged in popularity, with the tool-calling feature dramatically expanding their capabilities beyond simple text generation. Now, LLMs can handle complex automation tasks such as dynamic UI creation and autonomous a
 How ADHD Games, Health Tools & AI Chatbots Are Transforming Global HealthApr 14, 2025 am 11:27 AM
How ADHD Games, Health Tools & AI Chatbots Are Transforming Global HealthApr 14, 2025 am 11:27 AMCan a video game ease anxiety, build focus, or support a child with ADHD? As healthcare challenges surge globally — especially among youth — innovators are turning to an unlikely tool: video games. Now one of the world’s largest entertainment indus
 UN Input On AI: Winners, Losers, And OpportunitiesApr 14, 2025 am 11:25 AM
UN Input On AI: Winners, Losers, And OpportunitiesApr 14, 2025 am 11:25 AM“History has shown that while technological progress drives economic growth, it does not on its own ensure equitable income distribution or promote inclusive human development,” writes Rebeca Grynspan, Secretary-General of UNCTAD, in the preamble.
 Learning Negotiation Skills Via Generative AIApr 14, 2025 am 11:23 AM
Learning Negotiation Skills Via Generative AIApr 14, 2025 am 11:23 AMEasy-peasy, use generative AI as your negotiation tutor and sparring partner. Let’s talk about it. This analysis of an innovative AI breakthrough is part of my ongoing Forbes column coverage on the latest in AI, including identifying and explaining
 TED Reveals From OpenAI, Google, Meta Heads To Court, Selfie With MyselfApr 14, 2025 am 11:22 AM
TED Reveals From OpenAI, Google, Meta Heads To Court, Selfie With MyselfApr 14, 2025 am 11:22 AMThe TED2025 Conference, held in Vancouver, wrapped its 36th edition yesterday, April 11. It featured 80 speakers from more than 60 countries, including Sam Altman, Eric Schmidt, and Palmer Luckey. TED’s theme, “humanity reimagined,” was tailor made
 Joseph Stiglitz Warns Of The Looming Inequality Amid AI Monopoly PowerApr 14, 2025 am 11:21 AM
Joseph Stiglitz Warns Of The Looming Inequality Amid AI Monopoly PowerApr 14, 2025 am 11:21 AMJoseph Stiglitz is renowned economist and recipient of the Nobel Prize in Economics in 2001. Stiglitz posits that AI can worsen existing inequalities and consolidated power in the hands of a few dominant corporations, ultimately undermining economic
 What is Graph Database?Apr 14, 2025 am 11:19 AM
What is Graph Database?Apr 14, 2025 am 11:19 AMGraph Databases: Revolutionizing Data Management Through Relationships As data expands and its characteristics evolve across various fields, graph databases are emerging as transformative solutions for managing interconnected data. Unlike traditional
 LLM Routing: Strategies, Techniques, and Python ImplementationApr 14, 2025 am 11:14 AM
LLM Routing: Strategies, Techniques, and Python ImplementationApr 14, 2025 am 11:14 AMLarge Language Model (LLM) Routing: Optimizing Performance Through Intelligent Task Distribution The rapidly evolving landscape of LLMs presents a diverse range of models, each with unique strengths and weaknesses. Some excel at creative content gen


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment




