bitsCN.com
MySQL Internals-Index Merge优化
Louis Hust
0 前言
之前搞错了,以为Index Merge是MySQL5.6的新特性,原来不是,发现5.5也有,看了下manual,发现5.0的manual就已经存在了, 可以说是一个历史悠久的优化手段了,好吧,不管怎么样,今天就拨开其神秘的面纱,看看其内部到底如何生成这种Index Merge的计划的。 这里只详细介绍Intersect操作,对于Union和Sort-Union的具体代码,还没开始研究。
1 Index Merge理论基础
Index Merge——索引归并,即针对一张表,同时使用多个索引进行查询,然后将各个索引查出来的结果进行进一步的操作,可以是求交 ——Intersect,也可以是求和——Union,针对union还有一种补充算法——Sort-Union,很奇怪为什么没有Sort-Intersect,按道理也是可以做的。
什么情况下,同时使用多个索引会有利呢?比如说WHERE条件是C1=10 AND C2 =100,但是只有分别针对C1和C2的索引,而没有(C1,C2)这种索引, 两个索引同时使用才有意义,通过两个索引都可以快速定位到一批数据,然后对这一批数据进行进一步的求交或求和操作即可,这样的效率可能比 全表扫描或者只使用其中一个索引进行扫描然后再去主索引查询要快。
Intersect和Union都需要使用的索引是ROR的,也就时ROWID ORDERED,即针对不同的索引扫描出来的数据必须是同时按照ROWID排序的,这里的 ROWID其实也就是InnoDB的主键(如果不定义主键,InnoDB会隐式添加ROWID列作为主键)。只有每个索引是ROR的,才能进行归并排序,你懂的。 当然你可能会有疑惑,查不记录后内部进行一次sort不一样么,何必必须要ROR呢,不错,所以有了SORT-UNION。SORT-UNION就是每个非ROR的索引 排序后再进行Merge。至于为什么没有SORT-INTERSECT,我也很是迷茫。
2 初始化数据
mysql> show create table im/G*************************** 1. row *************************** Table: imCreate Table: CREATE TABLE `im` ( `c1` int(11) DEFAULT NULL, `c2` int(11) DEFAULT NULL, `c3` int(11) DEFAULT NULL, KEY `c1` (`c1`,`c3`), KEY `c2` (`c2`,`c1`)) ENGINE=InnoDB DEFAULT CHARSET=latin11 row in set (0.00 sec)mysql> show create procedure fill_im1/G*************************** 1. row *************************** Procedure: fill_im1 sql_mode: NO_ENGINE_SUBSTITUTION Create Procedure: CREATE DEFINER=`root`@`127.0.0.1` PROCEDURE `fill_im1`(cnt int)begin declare i int default 0; repeat insert into im values(100, 50, 100); set i=i+1; until i > cnt end repeat; endcharacter_set_client: utf8collation_connection: utf8_general_ci Database Collation: latin1_swedish_ci1 row in set (0.07 sec)mysql> show create procedure fill_im2/G*************************** 1. row *************************** Procedure: fill_im2 sql_mode: NO_ENGINE_SUBSTITUTION Create Procedure: CREATE DEFINER=`root`@`127.0.0.1` PROCEDURE `fill_im2`(cnt int)begin declare i int default 0; repeat insert into im values(100, 100, 50); set i=i+1; until i > cnt end repeat; endcharacter_set_client: utf8collation_connection: utf8_general_ci Database Collation: latin1_swedish_ci1 row in set (0.00 sec)mysql> call fill_im1(2000)mysql> call fill_im2(2000)mysql> insert into im values(100,50,50);Query OK, 1 row affected (0.00 sec)mysql> insert into im values(100,50,50);Query OK, 1 row affected (0.00 sec)mysql> commit;Query OK, 0 rows affected (0.05 sec)mysql> select * from im where c1=100 and c2 = 50 and c3 = 50/G*************************** 1. row ***************************c1: 100c2: 50c3: 50*************************** 2. row ***************************c1: 100c2: 50c3: 502 rows in set (0.13 sec)
3 执行计划
mysql> explain select * from im where c1=100 and c2 = 50 and c3 = 50/G*************************** 1. row *************************** id: 1 select_type: SIMPLE table: im type: index_mergepossible_keys: c1,c2 key: c1,c2 key_len: 10,10 ref: NULL rows: 1001 Extra: Using intersect(c1,c2); Using where; Using index1 row in set (0.00 sec)
4 代码分析
从生成数据的方法可以看出来,是专门针对查询的语句进行构造的。无论是根据(c1,c3)的索引查询还是根据(c2,c1)的索引查询, 都会查出一般的数据,即效率接近于全表扫描的一半。但是如果利用两个索引同时进行过滤,那么过滤出来的数据就很少了,也就是 结果中的两条。
也就是说如果单独查询各个索引,过滤效果不明显,但是如果联合两个索引进行MERGE过滤,那么效果可能很明显,这里所说的过滤,用更 专业的词来说是选择因子——selectivity。而计划的选择时代价的计算,便是计算这个选择因子。如果综合多个索引,导致选择因子很小,从而 达到索引merge出来的结果集很小的话,那么计划就更倾向于Index Merge,反之则不然。
下面是选择子计算的代码:
static double ror_scan_selectivity(const ROR_INTERSECT_INFO *info, const ROR_SCAN_INFO *scan){ double selectivity_mult= 1.0; const TABLE * const table= info->param->table; const KEY_PART_INFO * const key_part= table->key_info[scan->keynr].key_part; /** key values tuple, used to store both min_range.key and max_range.key. This function is only called for equality ranges; open ranges (e.g. "min_value covered_fields, key_part->fieldnr-1)); key_range min_range; key_range max_range; min_range.key= key_val; min_range.flag= HA_READ_KEY_EXACT; max_range.key= key_val; max_range.flag= HA_READ_AFTER_KEY; ha_rows prev_records= table->file->stats.records; DBUG_ENTER("ror_scan_selectivity"); for (sel_arg= scan->sel_arg; sel_arg; sel_arg= sel_arg->next_key_part) { DBUG_PRINT("info",("sel_arg step")); cur_covered= test(bitmap_is_set(&info->covered_fields, key_part[sel_arg->part].fieldnr-1)); if (cur_covered != prev_covered) { /* create (part1val, ..., part{n-1}val) tuple. */ bool is_null_range= false; ha_rows records; if (!tuple_arg) { tuple_arg= scan->sel_arg; /* Here we use the length of the first key part */ tuple_arg->store_min(key_part[0].store_length, &key_ptr, 0); is_null_range|= tuple_arg->is_null_interval(); keypart_map= 1; } while (tuple_arg->next_key_part != sel_arg) { tuple_arg= tuple_arg->next_key_part; tuple_arg->store_min(key_part[tuple_arg->part].store_length, &key_ptr, 0); is_null_range|= tuple_arg->is_null_interval(); keypart_map= (keypart_map param->use_index_statistics || // (1) is_null_range || // (2) !(records= table->key_info[scan->keynr]. rec_per_key[tuple_arg->part])) // (3) { DBUG_EXECUTE_IF("crash_records_in_range", DBUG_SUICIDE();); DBUG_ASSERT(min_range.length > 0); records= (table->file-> records_in_range(scan->keynr, &min_range, &max_range)); } if (cur_covered) { /* uncovered -> covered */ double tmp= rows2double(records)/rows2double(prev_records); DBUG_PRINT("info", ("Selectivity multiplier: %g", tmp)); selectivity_mult *= tmp; prev_records= HA_POS_ERROR; } else { /* covered -> uncovered */ prev_records= records; } } prev_covered= cur_covered; } if (!prev_covered) { double tmp= rows2double(table->quick_rows[scan->keynr]) / rows2double(prev_records); DBUG_PRINT("info", ("Selectivity multiplier: %g", tmp)); selectivity_mult *= tmp; } // Todo: This assert fires in PB sysqa RQG tests. // DBUG_ASSERT(selectivity_mult <p>刚看到这段代码时,确实有点犯懵,代码的注释给了很大的帮助:</p><pre class="brush:php;toolbar:false">/* Get selectivity of adding a ROR scan to the ROR-intersection. SYNOPSIS ror_scan_selectivity() info ROR-interection, an intersection of ROR index scans scan ROR scan that may or may not improve the selectivity of 'info' NOTES Suppose we have conditions on several keys cond=k_11=c_11 AND k_12=c_12 AND ... // key_parts of first key in 'info' k_21=c_21 AND k_22=c_22 AND ... // key_parts of second key in 'info' ... k_n1=c_n1 AND k_n3=c_n3 AND ... (1) //key_parts of 'scan' where k_ij may be the same as any k_pq (i.e. keys may have common parts). Note that for ROR retrieval, only equality conditions are usable so there are no open ranges (e.g., k_ij > c_ij) in 'scan' or 'info' A full row is retrieved if entire condition holds. The recursive procedure for finding P(cond) is as follows: First step: Pick 1st part of 1st key and break conjunction (1) into two parts: cond= (k_11=c_11 AND R) Here R may still contain condition(s) equivalent to k_11=c_11. Nevertheless, the following holds: P(k_11=c_11 AND R) = P(k_11=c_11) * P(R | k_11=c_11). Mark k_11 as fixed field (and satisfied condition) F, save P(F), save R to be cond and proceed to recursion step. Recursion step: We have a set of fixed fields/satisfied conditions) F, probability P(F), and remaining conjunction R Pick next key part on current key and its condition "k_ij=c_ij". We will add "k_ij=c_ij" into F and update P(F). Lets denote k_ij as t, R = t AND R1, where R1 may still contain t. Then P((t AND R1)|F) = P(t|F) * P(R1|t|F) = P(t|F) * P(R1|(t AND F)) (2) (where '|' mean conditional probability, not "or") Consider the first multiplier in (2). One of the following holds: a) F contains condition on field used in t (i.e. t AND F = F). Then P(t|F) = 1 b) F doesn't contain condition on field used in t. Then F and t are considered independent. P(t|F) = P(t|(fields_before_t_in_key AND other_fields)) = = P(t|fields_before_t_in_key). P(t|fields_before_t_in_key) = #records(fields_before_t_in_key) / #records(fields_before_t_in_key, t) The second multiplier is calculated by applying this step recursively. IMPLEMENTATION This function calculates the result of application of the "recursion step" described above for all fixed key members of a single key, accumulating set of covered fields, selectivity, etc. The calculation is conducted as follows: Lets denote #records(keypart1, ... keypartK) as n_k. We need to calculate n_{k1} n_{k2} --------- * --------- * .... (3) n_{k1-1} n_{k2-1} where k1,k2,... are key parts which fields were not yet marked as fixed ( this is result of application of option b) of the recursion step for parts of a single key). Since it is reasonable to expect that most of the fields are not marked as fixed, we calculate (3) as n_{i1} n_{i2} (3) = n_{max_key_part} / ( --------- * --------- * .... ) n_{i1-1} n_{i2-1} where i1,i2, .. are key parts that were already marked as fixed. In order to minimize number of expensive records_in_range calls we group and reduce adjacent fractions. Note that on the optimizer's request, index statistics may be used instead of records_in_range @see RANGE_OPT_PARAM::use_index_statistics. RETURN Selectivity of given ROR scan, a number between 0 and 1. 1 means that adding 'scan' to the intersection does not improve the selectivity.*/ 注释想说明的就是选择因子的概率如何进行计算,其实就是不同INDEX之间差异性的索引列会引起选择因子不断变小,即 Index之间差异性越大,过滤的记录就越多,选择出来的数据集就会越少。INDEX的差异性就是INdex之间索引列列是否重复出现在 不同索引之间,两个INDEX约相似,那么MERGE的结果集越大。具体的实现大家自己看看吧,明白了原理,实现都是浮云了。
BTW, 5.6的Optimizer trace十分好用,对于想要跟踪Optimizer内部的同学来说,可以先把详细的计划生成流程通过Optimizer trace 打印出来,对照优化流程,就能更好的定位到代码。
References
- [1]
- index-merge-optimization
File translated fromTEXby TTH,version 4.03.
On 28 Jan 2013, 22:35.
 鸣潮沉没的历史5个灯塔位置介绍Mar 07, 2024 pm 03:58 PM
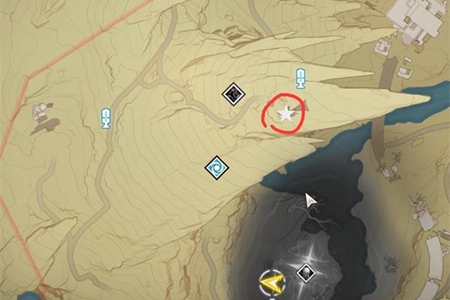
鸣潮沉没的历史5个灯塔位置介绍Mar 07, 2024 pm 03:58 PM您是否正在寻找《鸣潮沉没的历史》任务中的五个灯塔?本篇攻略将为您详尽解读这些待发现的灯塔所在之地。我们期望这能助您快速找到所需灯塔,顺利完成任务!鸣潮沉没的历史5个灯塔位置介绍具体位置一览:1、第一座灯塔:请您前往荒石高地,位于北落野正上方处。2、第二座灯塔:接下来请您赴中曲台地,在东北侧传送点周围便可寻见。3、第三座灯塔:请到虎口山脉东南方位,沿着无明湾即可找到。4、第四座灯塔:请您前往怨鸟泽东南方路端传送点,接近山崖之处。5、第五座灯塔:请至无光之森第一无音区,悬崖边缘即为所寻。
 如何查看和管理 Linux 命令历史记录Aug 01, 2023 pm 09:17 PM
如何查看和管理 Linux 命令历史记录Aug 01, 2023 pm 09:17 PM如何在Linux中查看命令历史记录在Linux中,我们使用history命令来查看所有以前执行的命令的列表。它有一个非常简单的语法:history与历史记录命令配对的一些选项包括:选项描述-c清除当前会话的命令历史记录-w将命令历史记录写入文件-r从历史记录文件重新加载命令历史记录-n限制最近命令的输出数量只需运行history命令即可在Linux终端中查看所有以前执行的命令的列表:除了查看命令历史记录之外,您还可以管理命令历史记录并执行修改先前执行的命令、反向搜索命令历史记录甚至完全删除历史记
 Go语言的历史发展及重要里程碑Apr 04, 2024 am 08:12 AM
Go语言的历史发展及重要里程碑Apr 04, 2024 am 08:12 AMGo语言由谷歌开发,最初于2007年构思,2012年发布1.0版本。其关键里程碑包括:2012年:发布Go1.0,引入并发性、内存安全和垃圾回收。2020年:Go2发布,引入模块化、协程改进和对泛型和错误处理的支持。2022年:Go1.19发布,提供性能优化和对泛型类型和一起函数的支持。
 快手历史亲密关系怎么看Apr 01, 2024 pm 04:51 PM
快手历史亲密关系怎么看Apr 01, 2024 pm 04:51 PM快手历史亲密关系允许用户将自己与特定好友之间的亲密程度标注在用户资料页上,从而展示出彼此之间的亲密关系,但是历史上的关系怎么看呢?如果你想知道的话,小编今天分享的教程你可以学习下吧。快手历史亲密关系查看方法第一步、打开快手个人主页,点击上方【亲密关系】图标。第二步、进入我的亲密朋友界面,点击亲密好友右侧【亲密值】图标。第三步、进入亲密值详情页,找到【亲密印记】卡片,即可查看建立亲密关系时间。
 凤凰新闻如何查看历史 查看历史记录的方法Mar 12, 2024 pm 07:16 PM
凤凰新闻如何查看历史 查看历史记录的方法Mar 12, 2024 pm 07:16 PM我们大家在这款凤凰新闻APP当中,都是会有机会让大家了解到各种各样的一些新闻资讯,这里的信息资源超多,各种各样的一些热点事件,都能够全部的掌握到,所以大家即时不出门,一样的都能够知晓天下大小事,绝对都是不会落后,很多的一些时候,都能够发现这里的新闻版块超多,各种的一些信息版块,随由大家自由的点击查看,当然大家有自己喜欢的一些版块领域,都能关注订阅一番,可以每一次都推荐出相关的一些资讯,非常的符合你们的需求,看的非常的满意,平常大家所看的这一些资讯,都能保存下来,大家可以随时的查看到自己的这一
 C语言的起源和发展历史Mar 18, 2024 pm 06:48 PM
C语言的起源和发展历史Mar 18, 2024 pm 06:48 PM标题:C语言的起源和发展历史C语言是一种广泛应用于系统软件和应用软件开发的高级编程语言。它具有结构化、模块化和可移植性等特点,是计算机领域中最为重要和流行的编程语言之一。本文将介绍C语言的起源和发展历史,并结合具体的代码示例进行说明。一、C语言的起源C语言的历史可以追溯到1969年,当时贝尔实验室的DennisRitchie和KenThompson为了开
 如何在iPhone上清除历史记录Jun 29, 2023 pm 01:13 PM
如何在iPhone上清除历史记录Jun 29, 2023 pm 01:13 PM如何在Safari中清除iPhone历史记录?要清除Apple的Safari上的浏览和搜索历史记录,您需要在设备上打开“设置”应用程序。选择“设置”后,您需要向下滚动并选择Safari,然后将显示另一个菜单,您需要选择清除历史记录和网站数据。您现在需要从菜单中选择清除历史记录和数据,这将从Apple的Safari浏览器中删除所有搜索历史记录,浏览历史记录,cookie和数据。就是这样,所有以前的浏览历史记录和搜索历史记录现在都已从Safari中删除。如果您不想删除Safari中的所有搜索历史记录
 Linux 如何查看历史登陆用户记录?Feb 21, 2024 pm 05:09 PM
Linux 如何查看历史登陆用户记录?Feb 21, 2024 pm 05:09 PMLinux系统作为一个开源的操作系统,用户可以通过一些简单的命令来查看系统的历史登陆用户记录,这对于系统管理员来说是非常重要的维护任务之一。下面将介绍如何在Linux系统中查看历史登陆用户记录的几种方法。1.使用last命令last命令可以显示最近登陆用户的历史记录。在终端中输入以下命令:last系统将显示最近登陆用户的历史记录,包括用户名、登


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Atom editor mac version download
The most popular open source editor

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

SublimeText3 Linux new version
SublimeText3 Linux latest version

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment







