Home >Technology peripherals >AI >Schram's sorting - learning to sort based on fairness
Schram's sorting - learning to sort based on fairness
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBforward
- 2024-02-07 14:50:31809browse
At the international academic conference AIBT 2023 held in 2023, Ratidar Technologies LLC published a fairness-based ranking learning algorithm and won the conference’s best paper report award. The algorithm, called Skellam Rank, makes full use of statistical principles and combines Pairwise Ranking and matrix decomposition technology to solve the accuracy and fairness problems in the recommendation system. Since there are few innovative ranking learning algorithms in recommender systems, Schramam's ranking algorithm performed so well that it won a research award at the conference. The basic principles of Schram's algorithm will be introduced below:
Let's first recall the Poisson distribution:
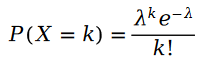
The calculation formula of the parameters of the Poisson distribution is as follows:
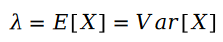
The difference between two Poisson variables is the Schillam distribution:
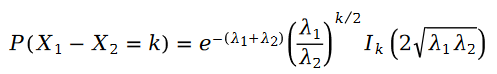
In the formula, we have:
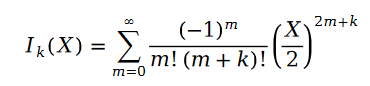
The function is called Bessel functions of the first kind.
With these basic concepts in statistics, let’s build a Pairwise Ranking ranking learning recommendation system!
We first believe that the user's rating of items is a Poisson distribution concept. In other words, the user's item rating value obeys the following probability distribution:
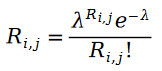
The reason why we can describe the process of users rating items as a Poisson process , because there is a Matthew effect in user item ratings, that is to say, the higher the user rating, the more people rate it, so that we can use the number of people who rated an item to approximate the distribution of the item's ratings. What random process does the number of people who rate an item obey? Naturally, we will think of the Poisson process. Because the probability of a user rating an item is similar to the probability of how many people have rated the item, we can naturally use the Poisson process to approximate the process of users rating an item.
Let’s replace the parameters of the Poisson process with the statistics of the sample data and get the following formula:
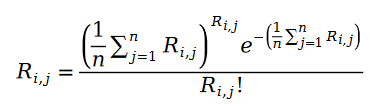
We define the maximum likelihood function formula of Pariwise Ranking below. As we all know, the so-called Pairwise Ranking means that we use the maximum likelihood function to solve the model parameters so that the model can maintain the relationship of the known ranking pairs in the data sample to the greatest extent:
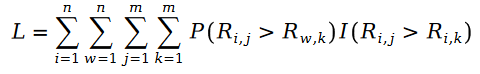
Because R in the formula is a Poisson distribution, their difference is the Schramam distribution, that is to say:
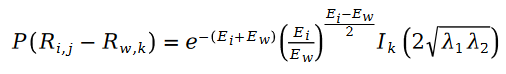
The variable E is defined as follows:
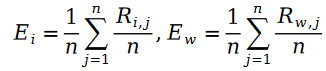
We bring the formula of Schram distribution into the maximum likelihood function The loss function L, the following formula is obtained:
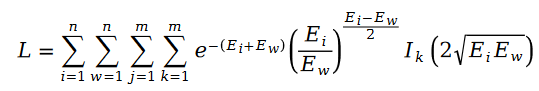
#For the user rating value R that appears in the variable E, we use matrix decomposition to solve it . Use the parameter user feature vector U and item feature vector V in matrix decomposition as variables to be solved:
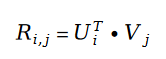
Here we first review the concept of matrix decomposition. The concept of matrix factorization is a recommendation system algorithm proposed around 2010. This algorithm can be said to be one of the most successful recommendation system algorithms in history. To this day, a large number of recommendation system companies still use matrix decomposition algorithm as the baseline of online systems, and Factorization Machine, an important component in the popular classic recommendation algorithm DeepFM, is also a subsequent improvement of the matrix decomposition algorithm in the recommendation system algorithm. Version is inextricably linked to matrix decomposition. There is a landmark paper on the matrix factorization algorithm, which is Probabilistic Matrix Factorization in 2007. The author used a statistical learning model to remodel the concept of matrix factorization in linear algebra, giving matrix factorization a solid mathematical theoretical foundation for the first time.
The basic concept of matrix decomposition is to use the dot product of vectors to efficiently predict unknown user ratings while reducing the dimensionality of the user rating matrix. The loss function of matrix decomposition is as follows:
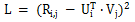
There are many variants of matrix decomposition algorithm, such as SVDFeature proposed by Shanghai Jiaotong University, which uses linear Modeling in the form of combination turns the problem of matrix decomposition into a problem of feature engineering. SVDFeature is also a landmark paper in the field of matrix factorization. Matrix decomposition can be applied in Pairwise Ranking to replace unknown user ratings to achieve modeling purposes. Classic application cases include the BPR-MF algorithm in Bayesian Pairwise Ranking, and the Schramam ranking algorithm draws on the same ideas.
We use stochastic gradient descent to solve the Schramam sorting algorithm. Because stochastic gradient descent can greatly simplify the loss function during the solution process to achieve the purpose of solution, our loss function becomes the following formula:
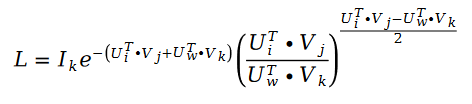
Using stochastic gradient descent to solve the unknown parameters U and V, we get the iterative formula as follows:
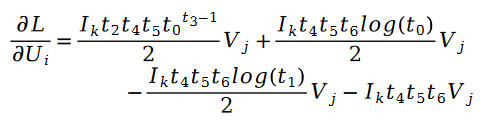
where:
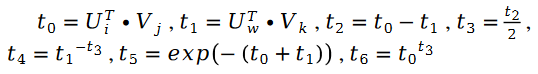
In addition:
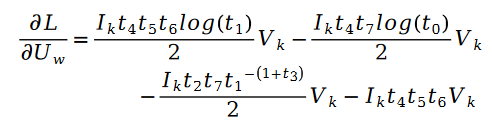
Among them:
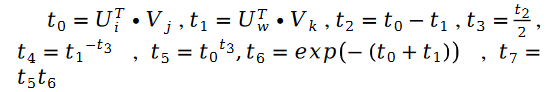
The solution to the unknown parameter variable V is similar, we have the following formula:
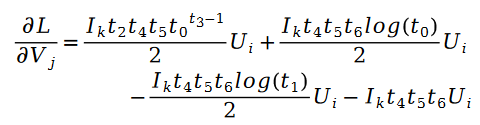
Among them:
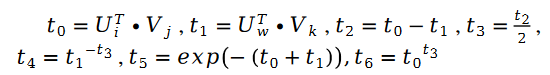
In addition:
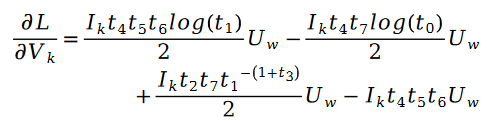
Among them:
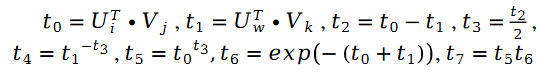
We use the following pseudo code to demonstrate the entire algorithm process:

In order to verify the effectiveness of the algorithm, the author of the paper conducted tests on MovieLens 1 Million Dataset and LDOS-CoMoDa Dataset. The first data set contains ratings of 6040 users and 3706 movies. The entire rating data set has approximately 1 million rating data and is one of the most well-known rating data collections in the field of recommendation systems. The second data collection comes from Slovenia and is a scenario-based recommendation system data collection that is rare on the Internet. The data set contains ratings from 121 users and 1232 movies. The author compared Schram's sorting with 9 other recommendation system algorithms. The main evaluation indicators are MAE (Mean Absolute Error, used to test accuracy) and Degree of Matthew Effect (mainly used to test fairness):
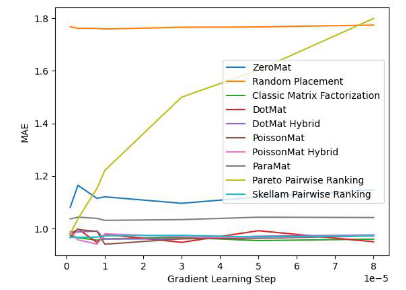
Figure 1. MovieLens 1 Million Dataset (MAE indicator)
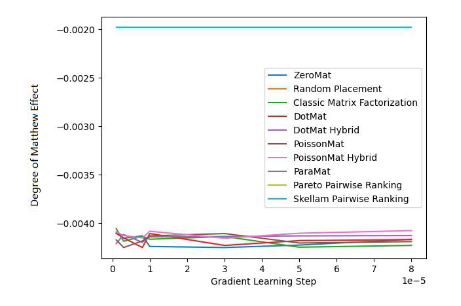
Figure 2. MovieLens 1 Million Dataset (Degree of Matthew Effect indicator)
Through Figure 1 and Figure 2, we found that Skilam sorting performed well on the MAE indicator. , but during the entire experimental process of Grid Search, there is no guarantee that the performance will be better than other algorithms. But in Figure 2, we find that Schram's sorting leads the way in the fairness index, far ahead of the other 9 recommendation system algorithms.
Let’s take a look at the performance of this algorithm on the LDOS-CoMoDa data set:
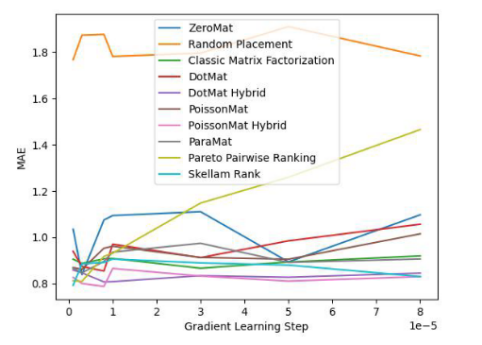
Figure 3. LDOS-CoMoDa Dataset (MAE indicator)
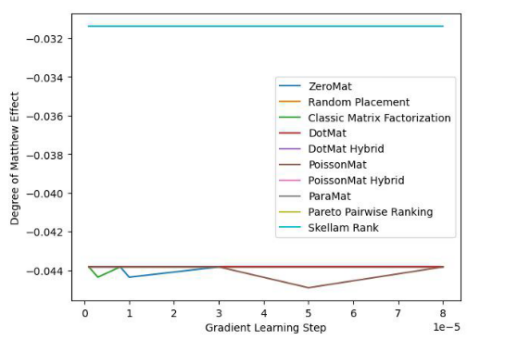
##Figure 4. LDOS-CoMoDa Dataset (Degree of Matthew Effect indicator)
Through Figure 3 and Figure 4, we understand that Schram's sorting is unparalleled in the fairness index and performs well in the accuracy index. The conclusion is similar to the previous experiment.
Schillam sorting combines concepts such as Poisson distribution, matrix decomposition and Pairwise Ranking, and is a rare ranking learning algorithm for recommendation systems. In the technical field, those who master ranking learning technology only account for 1/6 of those who master deep learning, so ranking learning is a scarce technology. And there are even fewer talents who can invent original ranking learning in the field of recommendation systems. The ranking learning algorithm liberates people from the narrow perspective of score prediction and makes people realize that the most important thing is the order, not the score. Ranking learning based on fairness is currently very popular in the field of information retrieval, especially in top conferences such as SIGIR. Papers on recommendation systems based on fairness are very welcome and hope to get the attention of readers.
About the author
Wang Hao, former head of Funplus Artificial Intelligence Laboratory. He has held technology and technology executive positions in ThoughtWorks, Douban, Baidu, Sina and other companies. Having worked in Internet companies, financial technology, gaming and other companies for 12 years, he has deep insights and rich experience in fields such as artificial intelligence, computer graphics and blockchain. Published 42 papers in international academic conferences and journals, and won the IEEE SMI 2008 Best Paper Award and the ICBDT 2020 / IEEE ICISCAE 2021 / AIBT 2023 Best Paper Report Award.
The above is the detailed content of Schram's sorting - learning to sort based on fairness. For more information, please follow other related articles on the PHP Chinese website!

