The details of Microsoft’s AIOps work revealed

introduce

Dynamic measurement, these data are mainly divided into two categories: time series data and event data. Time series data refers to real-valued time series (usually with fixed time intervals), such as CPU usage, etc.; while event data refers to the sequence that records the occurrence of specific events, such as memory overflow events. In order to ensure product service quality, reduce service downtime, and avoid greater economic losses, the diagnosis of key service events is particularly important. In actual operation and maintenance work, when diagnosing service events, operation and maintenance personnel can analyze the cause of the event by analyzing the time series data related to the service event. Although this correlation cannot completely accurately reflect the true cause-and-effect relationship, it can still provide some good clues and revelations for diagnosis.

Then the question is, how to automatically determine the relationship between events and time series data?

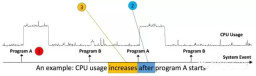
question

In this article, the author transforms the problem of event (E) and time series (S) data correlation into a two-sample problem, and uses the nearest neighbor method to determine whether they are related. Mainly answered three questions: A. Is there a correlation between E and S? B． If there is a correlation, what is the chronological order of E and S? E happens first, or S happens first? C． The monotonic relationship between E and S. Assuming that S (or E) occurs first, does the increase or decrease of S cause E to occur? As shown in the figure, the events are the running of programs A and B, and the timing data is the CPU usage. It can be found that there is a correlation between the event (running of program A) and the timing data (CPU usage), and it is the change in CPU usage that increases after program A is run.

method

The algorithm architecture of the article is mainly divided into three parts to solve the three problems of correlation, time sequence and monotonicity respectively. These three parts will be introduced in detail next.

Correlation

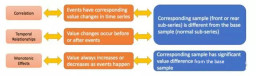
The article transforms the judgment of correlation into a two-sample problem. The core of the two-sample hypothesis test is to determine whether the two samples come from the same distribution. First, select N segments of time series sample data with length k corresponding before (or after) the event, represented by A1. Sample group A2 randomly selects a series of sample data of length k from the time series. The sample set is A1 and goes up to A2. If E and S are related, then the distributions of A1 and A2 are different, otherwise the distributions are the same. How to determine whether the distributions of A1 and A2 are the same? Let’s look at the following example:

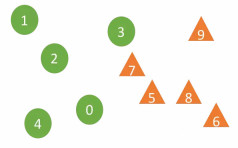
In the above figure, samples 0-4 are from sample group A1, and 5-9 belong to sample group A2. The DTW algorithm is used to calculate the distance between the two samples (the DTW algorithm can be well adapted to the scaling of sequence data and displacement). For a sample X belonging to sample group Ai (i=1 or 2), for the r nearest neighbor samples of E and S are more related. For example, if the number of neighbors is r=2, the two nearest neighbors of sample 7 are 3 and 5 from two different sample groups, but the two nearest neighbors of sample 5 are 7 and 8 from the same sample group A2. The article uses the confidence coefficient (Confident coefficient) to judge the credibility of "hypothesis test H1" (the two distributions are not the same, that is, E and S are related). The greater the confidence coefficient, the more credible H1 is. There are two key parameters of the algorithm: the number of nearest neighbors r and the time series length k. The number of neighbors is the natural logarithm of the number of samples. The first peak of the autocorrelation function curve of time series data is the sequence length.

Time sequence

Select the sequence before and after the event and the randomly selected time series to calculate the correlation. The results are Dr and Df. If Dr is True and Df is False, it means that E occurs before S occurs (E -> S). If Dr is False and Df is True, or Dr is True and Df is True, it means that S occurs before E occurs (S -> E). As shown in the example below, the event CPU Intensive Program -> time series data CPU Usage, the time series data CPU Usage -> event SQL Query Alert.

Monotone relationship

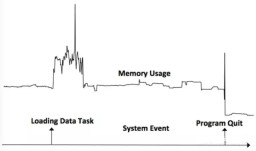
Monotonicity is judged by the changes in the time series before and after the event occurs. If the time series after the event occurs is larger than the value of the previous sequence, the monotonicity is increased, otherwise it is decreased. As shown in the figure below, the event loading Data Task caused an increase in Memory Usage, and the event Program Quit caused a decrease in Memory Usage.

Experimental results

The article verifies the algorithm performance by using Microsoft's system monitoring data and data from the customer service team. The data are 24 S (memory, CPU and DISK data) and 52 E (execution of specific tasks), 7 S (HTTP status code) and 57 E (service subject), the evaluation standard is F-score. The results show that the DTW distance performs better overall than other distances (L1 and L2), and the algorithm overall performs better than the two baseline algorithms (Pearson correlation and J-Measure).

in conclusion

The article introduces a new unsupervised method to study the relationship between events and time series data, answering three questions: Are E and S related? What order did E and S occur? And what is a monotonic relationship? Compared with many current correlation studies, which mainly focus on the correlation between events and the correlation between time series data, this article focuses on the relationship between events and time series data. It is the first to answer the above three questions between events and time series data. problem work.

Event diagnosis has always been a very important task in the field of operation and maintenance. The correlation between events and time series data can not only provide good inspiration for event diagnosis, but also provide good clues for root cause analysis. The author verified the algorithm on Microsoft's internal data set and achieved good results, which is of high value to both academic and industrial circles.

The above is the detailed content of The details of Microsoft’s AIOps work revealed. For more information, please follow other related articles on the PHP Chinese website!