 Backend Development
Backend Development Python Tutorial
Python Tutorial Using Python to implement the running steps of the shuffling algorithm
Using Python to implement the running steps of the shuffling algorithm
给定一个数组,编写一个程序来生成数组元素的随机排列,这个问题也被称为“洗牌”或“随机化给定的数组”。洗牌算法中数组元素的每种排列的可能性都应该是相同的。
洗牌算法是如何运行的
给定的数组是arr[],一个简单的解决方法是创建一个辅助数组temp[],它最初是arr[]的副本。从temp[]中随机选择一个元素,将随机选择的元素复制到arr[0],然后从temp[]中删除选择的元素。重复相同的过程n次并继续将元素复制到arr[1]、arr[2]、...。该解决方案的时间复杂度为O(n^2)。
Fisher-Yates shuffle算法的工作时间复杂度为O(n)。这里的假设是,我们得到一个函数rand(),它在O(1)时间内生成一个随机数。这个想法是从最后一个元素开始,并将其与整个数组(包括最后一个)中随机选择的元素交换。现在考虑从0到n-2的数组(大小减1),重复这个过程直到我们找到第一个元素。
下面是详细的算法:
对包含n个元素(索引0..n-1)的数组a进行洗牌
for i from n-1 downto 1 do j=random integer with 0<=j<=i exchange a[j]and a<i>
Python实现洗牌算法
from random import randint def randomize(arr,n): for i in range(n-1,0,-1): j=randint(0,i+1) arr<i>,arr[j]=arr[j],arr<i> return arr arr=[1,2,3,4,5,6,7,8] n=len(arr) print(randomize(arr,n)) 输出结果:7 8 4 6 3 1 2 5
The above is the detailed content of Using Python to implement the running steps of the shuffling algorithm. For more information, please follow other related articles on the PHP Chinese website!
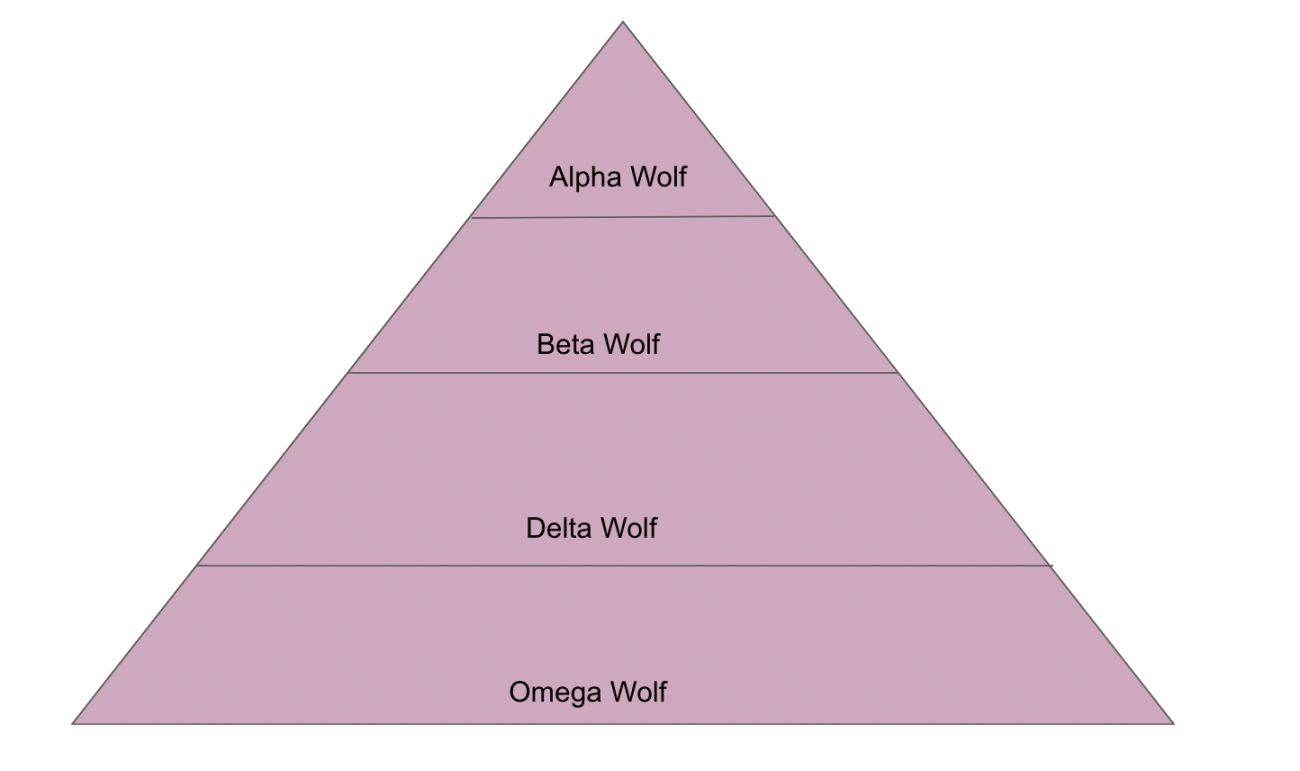 深入剖析灰狼优化算法(GWO)及其优势与弱点Jan 19, 2024 pm 07:48 PM
深入剖析灰狼优化算法(GWO)及其优势与弱点Jan 19, 2024 pm 07:48 PM灰狼优化算法(GWO)是一种基于种群的元启发式算法,模拟自然界中灰狼的领导层级和狩猎机制。灰狼算法灵感1、灰狼被认为是顶级掠食者,处于食物链的顶端。2、灰狼喜欢群居(群居),每个狼群平均有5-12只狼。3、灰狼具有非常严格的社会支配等级,如下图:Alpha狼:Alpha狼在整个灰狼群中占据优势地位,拥有统领整个灰狼群的权利。在算法应用中,Alpha狼是最佳解决方案之一,由优化算法产生的最优解。Beta狼:Beta狼定期向Alpha狼报告,并帮助Alpha狼做出最佳决策。在算法应用中,Beta狼可
 解析麻雀搜索算法(SSA)的原理、模型和构成Jan 19, 2024 pm 10:27 PM
解析麻雀搜索算法(SSA)的原理、模型和构成Jan 19, 2024 pm 10:27 PM麻雀搜索算法(SSA)是基于麻雀反捕食和觅食行为的元启发式优化算法。麻雀的觅食行为可分为两种主要类型:生产者和拾荒者。生产者主动寻找食物,而拾荒者则争夺生产者的食物。麻雀搜索算法(SSA)原理在麻雀搜索算法(SSA)中,每只麻雀都密切关注着邻居的行为。通过采用不同的觅食策略,个体能够有效地利用保留的能量来追求更多的食物。此外,鸟类在搜索空间中更容易受到捕食者的攻击,因此它们需要寻找更安全的位置。群体中心的鸟类可以通过靠近邻居来最大限度地减少自身的危险范围。当一只鸟发现捕食者时,会发出警报声,以便
 探究嵌套采样算法的基本原理和实施流程Jan 22, 2024 pm 09:51 PM
探究嵌套采样算法的基本原理和实施流程Jan 22, 2024 pm 09:51 PM嵌套采样算法是一种高效的贝叶斯统计推断算法,用于计算复杂概率分布下的积分或求和。它通过将参数空间分解为多个体积相等的超立方体,并逐步迭代地将其中一个最小体积的超立方体“推出”,然后用随机样本填充该超立方体,以更好地估计概率分布的积分值。通过不断迭代,嵌套采样算法可以得到高精度的积分值和参数空间的边界,从而可应用于模型比较、参数估计和模型选择等统计学问题。该算法的核心思想是将复杂的积分问题转化为一系列简单的积分问题,通过逐步缩小参数空间的体积,逼近真实的积分值。每个迭代步骤都通过随机采样从参数空间
 信息增益在id3算法中的作用是什么Jan 23, 2024 pm 11:27 PM
信息增益在id3算法中的作用是什么Jan 23, 2024 pm 11:27 PMID3算法是决策树学习中的基本算法之一。它通过计算每个特征的信息增益来选择最佳的分裂点,以生成一棵决策树。信息增益是ID3算法中的重要概念,用于衡量特征对分类任务的贡献。本文将详细介绍信息增益的概念、计算方法以及在ID3算法中的应用。一、信息熵的概念信息熵是信息论中的概念,衡量随机变量的不确定性。对于离散型随机变量X,其信息熵定义如下:H(X)=-\sum_{i=1}^{n}p(x_i)log_2p(x_i)其中,n代表随机变量X可能的取值个数,而p(x_i)表示随机变量X取值为x_i的概率。信
 鲸鱼优化算法 (WOA) 的数值优化原理和分析Jan 19, 2024 pm 07:27 PM
鲸鱼优化算法 (WOA) 的数值优化原理和分析Jan 19, 2024 pm 07:27 PM鲸鱼优化算法(WOA)是一种基于自然启发的元启发式优化算法,模拟了座头鲸的狩猎行为,用于数值问题的优化。鲸鱼优化算法(WOA)以一组随机解作为起点,通过每次迭代中搜索代理的位置更新,根据随机选择的搜索代理或迄今为止的最佳解决方案来进行优化。鲸鱼优化算法灵感鲸鱼优化算法的灵感源自座头鲸的狩猎行为。座头鲸喜欢的食物位于海面附近,如磷虾和鱼群。因此,座头鲸在狩猎时通过自下而上螺旋吐泡泡的方式,将食物聚集在一起形成泡泡网。在“向上螺旋”机动中,座头鲸下潜约12m,然后开始在猎物周围形成螺旋形气泡并向上游
 Wu-Manber算法简介及Python实现说明Jan 23, 2024 pm 07:03 PM
Wu-Manber算法简介及Python实现说明Jan 23, 2024 pm 07:03 PMWu-Manber算法是一种字符串匹配算法,用于高效地搜索字符串。它是一种混合算法,结合了Boyer-Moore和Knuth-Morris-Pratt算法的优势,可提供快速准确的模式匹配。Wu-Manber算法步骤1.创建一个哈希表,将模式的每个可能子字符串映射到该子字符串出现的模式位置。2.该哈希表用于快速识别文本中模式的潜在起始位置。3.遍历文本并将每个字符与模式中的相应字符进行比较。4.如果字符匹配,则可以移动到下一个字符并继续比较。5.如果字符不匹配,可以使用哈希表来确定在模式的下一个潜
 尺度转换不变特征(SIFT)算法Jan 22, 2024 pm 05:09 PM
尺度转换不变特征(SIFT)算法Jan 22, 2024 pm 05:09 PM尺度不变特征变换(SIFT)算法是一种用于图像处理和计算机视觉领域的特征提取算法。该算法于1999年提出,旨在提高计算机视觉系统中的物体识别和匹配性能。SIFT算法具有鲁棒性和准确性,被广泛应用于图像识别、三维重建、目标检测、视频跟踪等领域。它通过在多个尺度空间中检测关键点,并提取关键点周围的局部特征描述符来实现尺度不变性。SIFT算法的主要步骤包括尺度空间的构建、关键点检测、关键点定位、方向分配和特征描述符生成。通过这些步骤,SIFT算法能够提取出具有鲁棒性和独特性的特征,从而实现对图像的高效
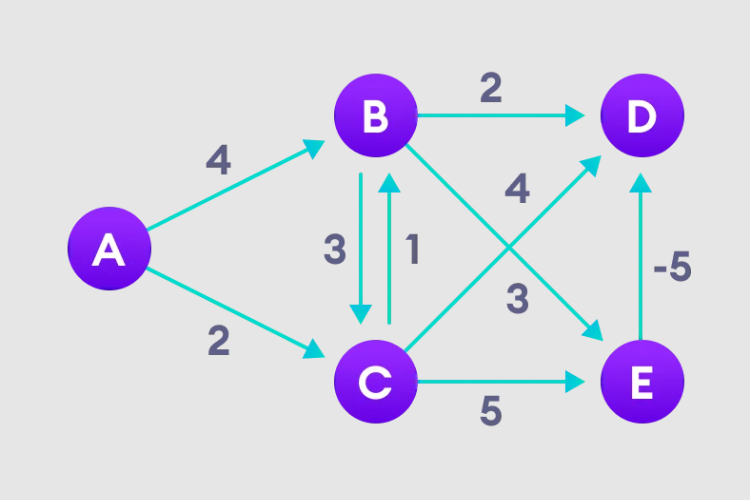 详解贝尔曼福特算法并用Python实现Jan 22, 2024 pm 07:39 PM
详解贝尔曼福特算法并用Python实现Jan 22, 2024 pm 07:39 PM贝尔曼福特算法(BellmanFord)可以找到从目标节点到加权图其他节点的最短路径。这一点和Dijkstra算法很相似,贝尔曼福特算法可以处理负权重的图,从实现来看也相对简单。贝尔曼福特算法原理详解贝尔曼福特算法通过高估从起始顶点到所有其他顶点的路径长度,迭代寻找比高估路径更短的新路径。因为我们要记录每个节点的路径距离,可以将其存储在大小为n的数组中,n也代表了节点的数量。实例图1、选择起始节点,并无限指定给其他所有顶点,记录路径值。2、访问每条边,并进行松弛操作,不断更新最短路径。3、我们需


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

Zend Studio 13.0.1
Powerful PHP integrated development environment

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),






