
In artificial neural networks, the sigmoid function is often used as the activation function of neurons to introduce nonlinear characteristics. This enables neural networks to learn more complex decision boundaries and play an important role in various applications such as image recognition, natural language processing, and speech recognition.
The sigmoid function is a commonly used mathematical function that can map any input value to a value between 0 and 1, so it has been widely used in binary classification and logistic regression problems. This function is characterized by an "S" shape that grows slowly at first, then quickly approaches 1, and eventually levels off.
Understanding the Sigmoid Function
The Sigmoid function is a commonly used mathematical function used to map input values to the range between 0 and 1. Its mathematical definition is 1/(1 e^(-x)), where x is the input value and e is the constant 2.718. This function is very useful in binary classification and logistic regression problems. Its value range is (0,1), and its domain is (-infinity, infinity). The characteristic of the S-shaped function is that it can convert any real input into a probability value, so it is often used in the output layer of the model in machine learning and statistics.
One of the key properties of the sigmoid function is that its output value exhibits an "S" shaped curve as the input value increases. As the input value increases, the output value gradually increases and eventually approaches 1. This feature provides important functionality for modeling decision boundaries in binary classification problems.
Another important property of the sigmoid function is its derivative, which plays a key role in neural network training. The derivative of the sigmoid function is defined as f(x)(1-f(x)), where f(x) represents the output of the function. The existence of derivatives enables the neural network to adjust the weights and biases of neurons more effectively, thereby improving the performance of the network. By calculating derivatives, the network can update parameters based on the gradient of the loss function, allowing the network to gradually optimize and improve accuracy. This method of using derivatives to train networks is widely used in the field of deep learning, allowing neural networks to learn and adapt to a variety of complex tasks.
In addition to the sigmoid function, there are other activation functions, such as ReLU and tanh, which can make up for the limitations of the sigmoid function. The output of the sigmoid function is always between 0 and 1, which can cause problems when the output of the network needs to be greater than 1 or less than 0. The ReLU function can solve this problem by mapping negative numbers to 0, while positive numbers remain unchanged. In addition, the tanh function is also a commonly used activation function. Its output range is between -1 and 1, which is more flexible than the sigmoid function. Therefore, when designing a neural network, different activation functions can be selected according to specific needs to achieve better results.
Using graphs to visualize the sigmoid function helps to better understand its properties. The graph shows the "S" shape taken by the function and how the output value changes as the input value changes.
Sigmoid function in artificial neural networks
The sigmoid function is usually used as the activation function of artificial neural networks. In a feedforward neural network, the output of each neuron is processed by a sigmoid function, which introduces nonlinear characteristics into the model. The introduction of nonlinear characteristics is important because it enables the neural network to learn more complex decision boundaries, thereby improving its performance on specific tasks.
Advantages:
- Produces output values between 0 and 1, which is helpful for binary classification and logistic regression problems.
- Differentiable means that its derivatives can be calculated, and it is easy to optimize the network by adjusting the weights and biases of neurons.
Disadvantages:
- It can produce output values close to 0 or 1, which may cause problems with the optimization algorithm.
- The gradient of the sigmoid function becomes very small near the output value 0 or 1, which makes it difficult for the optimization algorithm to adjust the weights and biases of the neurons.
The above is the detailed content of Application of sigmoid function in artificial neural network. For more information, please follow other related articles on the PHP Chinese website!
 解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM
解析二元神经网络的功能和原理Jan 22, 2024 pm 03:00 PM二元神经网络(BinaryNeuralNetworks,BNN)是一种神经网络,其神经元仅具有两个状态,即0或1。相对于传统的浮点数神经网络,BNN具有许多优点。首先,BNN可以利用二进制算术和逻辑运算,加快训练和推理速度。其次,BNN减少了内存和计算资源的需求,因为二进制数相对于浮点数来说需要更少的位数来表示。此外,BNN还具有提高模型的安全性和隐私性的潜力。由于BNN的权重和激活值仅为0或1,其模型参数更难以被攻击者分析和逆向工程。因此,BNN在一些对数据隐私和模型安全性有较高要求的应用中具
 探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM
探究RNN、LSTM和GRU的概念、区别和优劣Jan 22, 2024 pm 07:51 PM在时间序列数据中,观察之间存在依赖关系,因此它们不是相互独立的。然而,传统的神经网络将每个观察看作是独立的,这限制了模型对时间序列数据的建模能力。为了解决这个问题,循环神经网络(RNN)被引入,它引入了记忆的概念,通过在网络中建立数据点之间的依赖关系来捕捉时间序列数据的动态特性。通过循环连接,RNN可以将之前的信息传递到当前观察中,从而更好地预测未来的值。这使得RNN成为处理时间序列数据任务的强大工具。但是RNN是如何实现这种记忆的呢?RNN通过神经网络中的反馈回路实现记忆,这是RNN与传统神经
 计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PM
计算神经网络的浮点操作数(FLOPS)Jan 22, 2024 pm 07:21 PMFLOPS是计算机性能评估的标准之一,用来衡量每秒的浮点运算次数。在神经网络中,FLOPS常用于评估模型的计算复杂度和计算资源的利用率。它是一个重要的指标,用来衡量计算机的计算能力和效率。神经网络是一种复杂的模型,由多层神经元组成,用于进行数据分类、回归和聚类等任务。训练和推断神经网络需要进行大量的矩阵乘法、卷积等计算操作,因此计算复杂度非常高。FLOPS(FloatingPointOperationsperSecond)可以用来衡量神经网络的计算复杂度,从而评估模型的计算资源使用效率。FLOP
 模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM
模糊神经网络的定义和结构解析Jan 22, 2024 pm 09:09 PM模糊神经网络是一种将模糊逻辑和神经网络结合的混合模型,用于解决传统神经网络难以处理的模糊或不确定性问题。它的设计受到人类认知中模糊性和不确定性的启发,因此被广泛应用于控制系统、模式识别、数据挖掘等领域。模糊神经网络的基本架构由模糊子系统和神经子系统组成。模糊子系统利用模糊逻辑对输入数据进行处理,将其转化为模糊集合,以表达输入数据的模糊性和不确定性。神经子系统则利用神经网络对模糊集合进行处理,用于分类、回归或聚类等任务。模糊子系统和神经子系统之间的相互作用使得模糊神经网络具备更强大的处理能力,能够
 改进的RMSprop算法Jan 22, 2024 pm 05:18 PM
改进的RMSprop算法Jan 22, 2024 pm 05:18 PMRMSprop是一种广泛使用的优化器,用于更新神经网络的权重。它是由GeoffreyHinton等人在2012年提出的,并且是Adam优化器的前身。RMSprop优化器的出现主要是为了解决SGD梯度下降算法中遇到的一些问题,例如梯度消失和梯度爆炸。通过使用RMSprop优化器,可以有效地调整学习速率,并且自适应地更新权重,从而提高深度学习模型的训练效果。RMSprop优化器的核心思想是对梯度进行加权平均,以使不同时间步的梯度对权重的更新产生不同的影响。具体而言,RMSprop会计算每个参数的平方
 浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM
浅层特征与深层特征的结合在实际应用中的示例Jan 22, 2024 pm 05:00 PM深度学习在计算机视觉领域取得了巨大成功,其中一项重要进展是使用深度卷积神经网络(CNN)进行图像分类。然而,深度CNN通常需要大量标记数据和计算资源。为了减少计算资源和标记数据的需求,研究人员开始研究如何融合浅层特征和深层特征以提高图像分类性能。这种融合方法可以利用浅层特征的高计算效率和深层特征的强表示能力。通过将两者结合,可以在保持较高分类准确性的同时降低计算成本和数据标记的要求。这种方法对于那些数据量较小或计算资源有限的应用场景尤为重要。通过深入研究浅层特征和深层特征的融合方法,我们可以进一
 蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM
蒸馏模型的基本概念Jan 22, 2024 pm 02:51 PM模型蒸馏是一种将大型复杂的神经网络模型(教师模型)的知识转移到小型简单的神经网络模型(学生模型)中的方法。通过这种方式,学生模型能够从教师模型中获得知识,并且在表现和泛化性能方面得到提升。通常情况下,大型神经网络模型(教师模型)在训练时需要消耗大量计算资源和时间。相比之下,小型神经网络模型(学生模型)具备更高的运行速度和更低的计算成本。为了提高学生模型的性能,同时保持较小的模型大小和计算成本,可以使用模型蒸馏技术将教师模型的知识转移给学生模型。这种转移过程可以通过将教师模型的输出概率分布作为学生
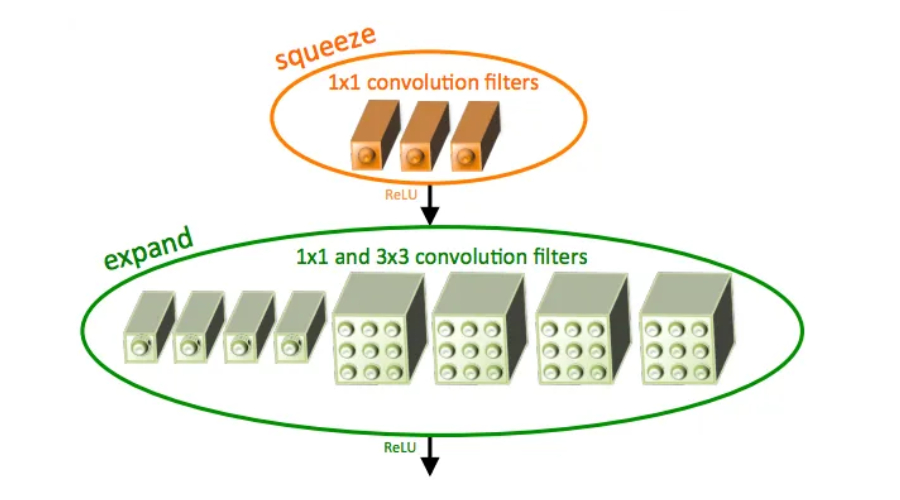 SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PM
SqueezeNet简介及其特点Jan 22, 2024 pm 07:15 PMSqueezeNet是一种小巧而精确的算法,它在高精度和低复杂度之间达到了很好的平衡,因此非常适合资源有限的移动和嵌入式系统。2016年,DeepScale、加州大学伯克利分校和斯坦福大学的研究人员提出了一种紧凑高效的卷积神经网络(CNN)——SqueezeNet。近年来,研究人员对SqueezeNet进行了多次改进,其中包括SqueezeNetv1.1和SqueezeNetv2.0。这两个版本的改进不仅提高了准确性,还降低了计算成本。SqueezeNetv1.1在ImageNet数据集上的精度


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

Atom editor mac version download
The most popular open source editor

SublimeText3 Linux new version
SublimeText3 Linux latest version

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),







