 Technology peripherals
Technology peripherals AI
AI Introduction to machine learning optimizers - discussion of common optimizer types and applications
Introduction to machine learning optimizers - discussion of common optimizer types and applications
The optimizer is an optimization algorithm used to find parameter values that minimize the error to improve the accuracy of the model. In machine learning, an optimizer finds the best solution to a given problem by minimizing or maximizing a cost function.
In different algorithm models, there are many different types of optimizers, each of which has its unique advantages and disadvantages. The most common optimizers are gradient descent, stochastic gradient descent, stochastic gradient descent with momentum, adaptive gradient descent, and root mean square. Each optimizer has some adjustable parameter settings that can be adjusted to improve performance.
Common optimizer types
Gradient descent (GD)
Gradient descent is a A basic first-order optimization algorithm that relies on the first derivative of the loss function. It searches for the value of the minimum cost function by updating the weights of the learning algorithm and finds the most suitable parameter values corresponding to the global minimum. Through backpropagation, the loss is passed from one layer to another, and the parameters of the model are adjusted according to the loss to minimize the loss function.
This is one of the oldest and most common optimizers used in neural networks and is best suited for situations where the data is arranged in a way that has a convex optimization problem.
The gradient descent algorithm is very simple to implement, but there is a risk of getting stuck in a local minimum, that is, it will not converge to the minimum.
Stochastic Gradient Descent (SGD)
As an extension of the gradient descent algorithm, stochastic gradient descent overcomes some of the shortcomings of the gradient descent algorithm. In stochastic gradient descent, instead of getting the entire dataset every iteration, batches of data are randomly selected, which means that only a small number of samples are taken from the dataset.
Therefore, the stochastic gradient descent algorithm requires more iterations to reach the local minimum. As the number of iterations increases, the overall computation time increases. But even after increasing the number of iterations, the computational cost is still lower than the gradient descent optimizer.
Stochastic Gradient Descent with Momentum
From the above we know that the path taken by stochastic gradient descent will have a greater impact than gradient descent. noise, and the calculation time will be longer. To overcome this problem, we use stochastic gradient descent with momentum algorithm.
The role of momentum is to help the loss function converge faster. However, you should remember when using this algorithm that the learning rate decreases with high momentum.
Adaptive Gradient Descent (Adagrad)
The adaptive gradient descent algorithm is slightly different from other gradient descent algorithms. This is because the algorithm uses a different learning rate for each iteration. The learning rate changes depending on the differences in parameters during training. The greater the parameter change, the smaller the learning rate change.
The advantage of using adaptive gradient descent is that it eliminates the need to manually modify the learning rate, will reach convergence faster, and adaptive gradient descent is better than the gradient descent algorithm and its Variants will be more reliable.
But the adaptive gradient descent optimizer will monotonically reduce the learning rate, causing the learning rate to become very small. Due to the small learning rate, the model cannot obtain more improvements, which ultimately affects the accuracy of the model.
Root Mean Square (RMS Prop) Optimizer
Root Mean Square is one of the popular optimizers among deep learning enthusiasts. Although it has not been officially released, it is still well known in the community. Root mean square is also considered an improvement over adaptive gradient descent optimizers because it reduces the monotonically decreasing learning rate.
The root mean square algorithm mainly focuses on speeding up the optimization process by reducing the number of function evaluations to reach a local minimum. This algorithm keeps a moving average of the squared gradients for each weight and divides the gradients by the square root of the mean square.
Compared to the gradient descent algorithm, this algorithm converges quickly and requires fewer adjustments. The problem with the root mean square optimizer is that the learning rate must be defined manually, and its recommended values do not apply to all applications.
Adam optimizer
The name Adam comes from adaptive moment estimation. This optimization algorithm is a further extension of stochastic gradient descent and is used to update network weights during training. Instead of maintaining a single learning rate through stochastic gradient descent training, the Adam optimizer updates the learning rate of each network weight individually.
The Adam optimizer inherits the characteristics of adaptive gradient descent and root mean square algorithms. The algorithm is easy to implement, has faster runtime, has low memory requirements, and requires fewer adjustments than other optimization algorithms.
Optimizer usage
- Stochastic gradient descent can only be used in shallow networks.
- Except for stochastic gradient descent, other optimizers eventually converge one after another, among which the adam optimizer converges the fastest.
- Adaptive gradient descent can be used with sparse data.
- The Adam optimizer is considered the best algorithm among all the above algorithms.
The above are some of the optimizers that are widely used in machine learning tasks. Each optimizer has its advantages and disadvantages. Therefore, understanding the requirements of the task and the type of data that needs to be processed is crucial to choosing an optimizer and achieving excellent results. Crucial.
The above is the detailed content of Introduction to machine learning optimizers - discussion of common optimizer types and applications. For more information, please follow other related articles on the PHP Chinese website!
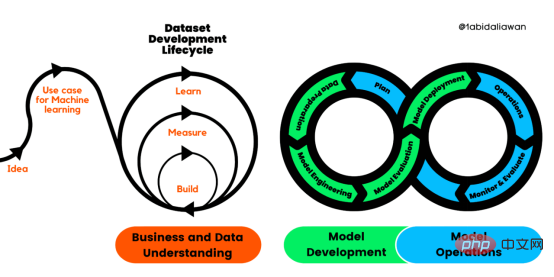 解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM
解读CRISP-ML(Q):机器学习生命周期流程Apr 08, 2023 pm 01:21 PM译者 | 布加迪审校 | 孙淑娟目前,没有用于构建和管理机器学习(ML)应用程序的标准实践。机器学习项目组织得不好,缺乏可重复性,而且从长远来看容易彻底失败。因此,我们需要一套流程来帮助自己在整个机器学习生命周期中保持质量、可持续性、稳健性和成本管理。图1. 机器学习开发生命周期流程使用质量保证方法开发机器学习应用程序的跨行业标准流程(CRISP-ML(Q))是CRISP-DM的升级版,以确保机器学习产品的质量。CRISP-ML(Q)有六个单独的阶段:1. 业务和数据理解2. 数据准备3. 模型
 2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM
2023年机器学习的十大概念和技术Apr 04, 2023 pm 12:30 PM机器学习是一个不断发展的学科,一直在创造新的想法和技术。本文罗列了2023年机器学习的十大概念和技术。 本文罗列了2023年机器学习的十大概念和技术。2023年机器学习的十大概念和技术是一个教计算机从数据中学习的过程,无需明确的编程。机器学习是一个不断发展的学科,一直在创造新的想法和技术。为了保持领先,数据科学家应该关注其中一些网站,以跟上最新的发展。这将有助于了解机器学习中的技术如何在实践中使用,并为自己的业务或工作领域中的可能应用提供想法。2023年机器学习的十大概念和技术:1. 深度神经网
 基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM
基于因果森林算法的决策定位应用Apr 08, 2023 am 11:21 AM译者 | 朱先忠审校 | 孙淑娟在我之前的博客中,我们已经了解了如何使用因果树来评估政策的异质处理效应。如果你还没有阅读过,我建议你在阅读本文前先读一遍,因为我们在本文中认为你已经了解了此文中的部分与本文相关的内容。为什么是异质处理效应(HTE:heterogenous treatment effects)呢?首先,对异质处理效应的估计允许我们根据它们的预期结果(疾病、公司收入、客户满意度等)选择提供处理(药物、广告、产品等)的用户(患者、用户、客户等)。换句话说,估计HTE有助于我
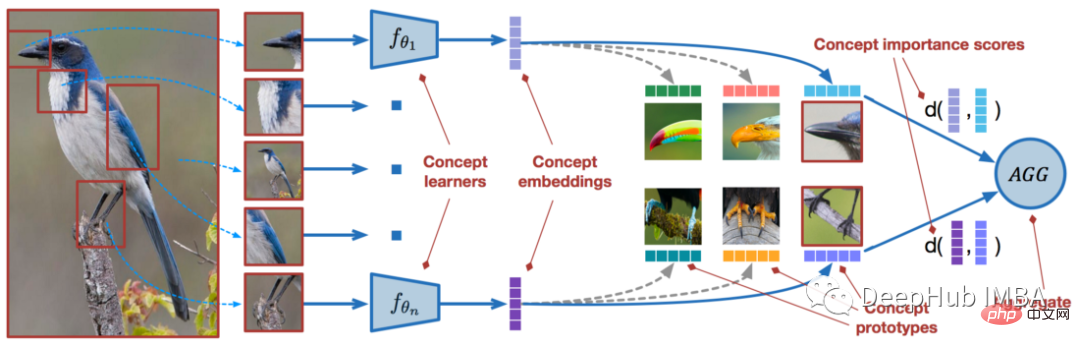 使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM
使用PyTorch进行小样本学习的图像分类Apr 09, 2023 am 10:51 AM近年来,基于深度学习的模型在目标检测和图像识别等任务中表现出色。像ImageNet这样具有挑战性的图像分类数据集,包含1000种不同的对象分类,现在一些模型已经超过了人类水平上。但是这些模型依赖于监督训练流程,标记训练数据的可用性对它们有重大影响,并且模型能够检测到的类别也仅限于它们接受训练的类。由于在训练过程中没有足够的标记图像用于所有类,这些模型在现实环境中可能不太有用。并且我们希望的模型能够识别它在训练期间没有见到过的类,因为几乎不可能在所有潜在对象的图像上进行训练。我们将从几个样本中学习
 LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM
LazyPredict:为你选择最佳ML模型!Apr 06, 2023 pm 08:45 PM本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。 摘要本文讨论使用LazyPredict来创建简单的ML模型。LazyPredict创建机器学习模型的特点是不需要大量的代码,同时在不修改参数的情况下进行多模型拟合,从而在众多模型中选出性能最佳的一个。本文包括的内容如下:简介LazyPredict模块的安装在分类模型中实施LazyPredict
 Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM
Mango:基于Python环境的贝叶斯优化新方法Apr 08, 2023 pm 12:44 PM译者 | 朱先忠审校 | 孙淑娟引言模型超参数(或模型设置)的优化可能是训练机器学习算法中最重要的一步,因为它可以找到最小化模型损失函数的最佳参数。这一步对于构建不易过拟合的泛化模型也是必不可少的。优化模型超参数的最著名技术是穷举网格搜索和随机网格搜索。在第一种方法中,搜索空间被定义为跨越每个模型超参数的域的网格。通过在网格的每个点上训练模型来获得最优超参数。尽管网格搜索非常容易实现,但它在计算上变得昂贵,尤其是当要优化的变量数量很大时。另一方面,随机网格搜索是一种更快的优化方法,可以提供更好的
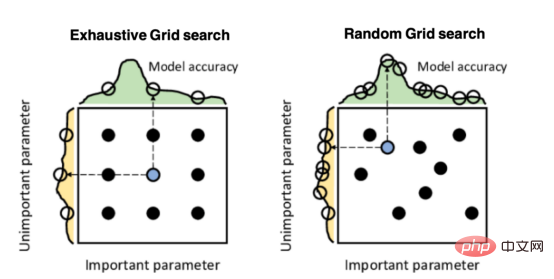
 超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM
超参数优化比较之网格搜索、随机搜索和贝叶斯优化Apr 04, 2023 pm 12:05 PM本文将详细介绍用来提高机器学习效果的最常见的超参数优化方法。 译者 | 朱先忠审校 | 孙淑娟简介通常,在尝试改进机器学习模型时,人们首先想到的解决方案是添加更多的训练数据。额外的数据通常是有帮助(在某些情况下除外)的,但生成高质量的数据可能非常昂贵。通过使用现有数据获得最佳模型性能,超参数优化可以节省我们的时间和资源。顾名思义,超参数优化是为机器学习模型确定最佳超参数组合以满足优化函数(即,给定研究中的数据集,最大化模型的性能)的过程。换句话说,每个模型都会提供多个有关选项的调整“按钮
 人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM
人工智能自动获取知识和技能,实现自我完善的过程是什么Aug 24, 2022 am 11:57 AM实现自我完善的过程是“机器学习”。机器学习是人工智能核心,是使计算机具有智能的根本途径;它使计算机能模拟人的学习行为,自动地通过学习来获取知识和技能,不断改善性能,实现自我完善。机器学习主要研究三方面问题:1、学习机理,人类获取知识、技能和抽象概念的天赋能力;2、学习方法,对生物学习机理进行简化的基础上,用计算的方法进行再现;3、学习系统,能够在一定程度上实现机器学习的系统。


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

SublimeText3 English version
Recommended: Win version, supports code prompts!

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment






