
Markov Chain Monte Carlo EM algorithm, referred to as MCMC-EM algorithm, is a statistical algorithm used for parameter estimation in unsupervised learning. Its core idea is to combine the Markov chain Monte Carlo method with the expectation maximization algorithm for parameter estimation of probability models with hidden variables. Through iteration, the MCMC-EM algorithm can gradually approach the maximum likelihood estimate of parameters. It is efficient and flexible and has been widely used in many fields.
The basic idea of the MCMC-EM algorithm is to use the MCMC method to obtain samples of hidden variables, use these samples to calculate the expected value, and then use the EM algorithm to maximize the log-likelihood function. The iterative process of this algorithm includes two steps: MCMC sampling and EM update. In the MCMC sampling step, we use the MCMC method to estimate the posterior distribution of the latent variables; while in the EM update step, we use the EM algorithm to estimate the model parameters. By alternating these two steps, we can continuously optimize the parameter estimates of the model. In summary, the MCMC-EM algorithm is an iterative algorithm that combines MCMC and EM for estimating the posterior distribution of model parameters and latent variables.
1.MCMC sampling
In the MCMC sampling step, you first need to select an initial state and pass the transition probability of the Markov chain Generate a sample sequence. A Markov chain is a sequence of states, each state is only related to the previous state, so as the sequence grows, the probability distribution of the current state tends to a stable distribution. In order to make the generated sample sequence tend to a stable distribution, appropriate transition probabilities need to be used in MCMC sampling. Common MCMC methods include Metropolis-Hastings algorithm and Gibbs sampling algorithm. These methods achieve sample generation and distribution approximation through different transition probabilities, thereby obtaining sampling of the target distribution. The Metropolis-Hastings algorithm uses an acceptance-rejection mechanism to decide whether to accept a transfer, while the Gibbs sampling algorithm uses a conditional distribution to make transfers. These methods are widely used in statistics and machine learning and can solve complex sampling and inference problems.
2.EM update
In the EM update step, you need to use the samples obtained by MCMC sampling to estimate the expected value of the latent variable, and use These expected values are used to maximize the log-likelihood function. The EM algorithm is an iterative algorithm, and each iteration includes two steps: E step and M step. In step E, it is necessary to calculate the posterior distribution of the latent variable and calculate the expected value of the latent variable. In step M, the expected value of the hidden variable calculated in step E needs to be used to maximize the log-likelihood function to solve for the maximum likelihood estimate of the parameters.
The advantage of the MCMC-EM algorithm is that it can better handle complex probability models, and can generate more samples through sampling methods to better estimate model parameters. In addition, the MCMC-EM algorithm can also balance sampling efficiency and sampling accuracy by adjusting the parameters of the MCMC method, thereby improving the performance of the algorithm.
However, the MCMC-EM algorithm also has some problems and challenges. First, the MCMC-EM algorithm requires a lot of computing resources and time, especially when processing large-scale data. Secondly, the MCMC-EM algorithm tends to converge slowly and requires many iterations to achieve convergence. Finally, the results of the MCMC-EM algorithm may be affected by the MCMC method selection and parameter settings, so appropriate debugging and optimization are required.
In general, the MCMC-EM algorithm is an important unsupervised learning algorithm and is widely used in fields such as parameter estimation and density estimation of probability models. Although there are some problems and challenges in the MCMC-EM algorithm, with the continuous improvement of computing resources and algorithm optimization, the MCMC-EM algorithm will become more practical and effective.
The above is the detailed content of Monte Carlo Markov chain EM algorithm. For more information, please follow other related articles on the PHP Chinese website!
 Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AM
Let's Dance: Structured Movement To Fine-Tune Our Human Neural NetsApr 27, 2025 am 11:09 AMScientists have extensively studied human and simpler neural networks (like those in C. elegans) to understand their functionality. However, a crucial question arises: how do we adapt our own neural networks to work effectively alongside novel AI s
 New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AM
New Google Leak Reveals Subscription Changes For Gemini AIApr 27, 2025 am 11:08 AMGoogle's Gemini Advanced: New Subscription Tiers on the Horizon Currently, accessing Gemini Advanced requires a $19.99/month Google One AI Premium plan. However, an Android Authority report hints at upcoming changes. Code within the latest Google P
 How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AM
How Data Analytics Acceleration Is Solving AI's Hidden BottleneckApr 27, 2025 am 11:07 AMDespite the hype surrounding advanced AI capabilities, a significant challenge lurks within enterprise AI deployments: data processing bottlenecks. While CEOs celebrate AI advancements, engineers grapple with slow query times, overloaded pipelines, a
 MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AM
MarkItDown MCP Can Convert Any Document into Markdowns!Apr 27, 2025 am 09:47 AMHandling documents is no longer just about opening files in your AI projects, it’s about transforming chaos into clarity. Docs such as PDFs, PowerPoints, and Word flood our workflows in every shape and size. Retrieving structured
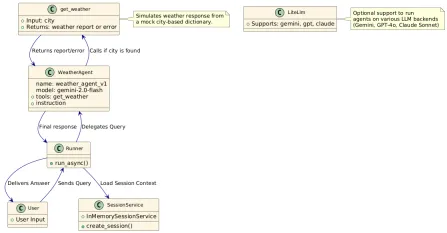 How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AM
How to Use Google ADK for Building Agents? - Analytics VidhyaApr 27, 2025 am 09:42 AMHarness the power of Google's Agent Development Kit (ADK) to create intelligent agents with real-world capabilities! This tutorial guides you through building conversational agents using ADK, supporting various language models like Gemini and GPT. W
 Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AM
Use of SLM over LLM for Effective Problem Solving - Analytics VidhyaApr 27, 2025 am 09:27 AMsummary: Small Language Model (SLM) is designed for efficiency. They are better than the Large Language Model (LLM) in resource-deficient, real-time and privacy-sensitive environments. Best for focus-based tasks, especially where domain specificity, controllability, and interpretability are more important than general knowledge or creativity. SLMs are not a replacement for LLMs, but they are ideal when precision, speed and cost-effectiveness are critical. Technology helps us achieve more with fewer resources. It has always been a promoter, not a driver. From the steam engine era to the Internet bubble era, the power of technology lies in the extent to which it helps us solve problems. Artificial intelligence (AI) and more recently generative AI are no exception
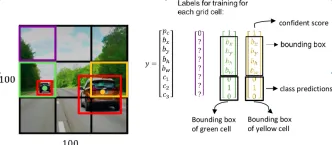 How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AM
How to Use Google Gemini Models for Computer Vision Tasks? - Analytics VidhyaApr 27, 2025 am 09:26 AMHarness the Power of Google Gemini for Computer Vision: A Comprehensive Guide Google Gemini, a leading AI chatbot, extends its capabilities beyond conversation to encompass powerful computer vision functionalities. This guide details how to utilize
 Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AM
Gemini 2.0 Flash vs o4-mini: Can Google Do Better Than OpenAI?Apr 27, 2025 am 09:20 AMThe AI landscape of 2025 is electrifying with the arrival of Google's Gemini 2.0 Flash and OpenAI's o4-mini. These cutting-edge models, launched weeks apart, boast comparable advanced features and impressive benchmark scores. This in-depth compariso


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

SublimeText3 Chinese version
Chinese version, very easy to use

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function






