How do deep residual networks overcome the vanishing gradient problem?

Residual network is a popular deep learning model that solves the vanishing gradient problem by introducing residual blocks. This article starts from the essential cause of the vanishing gradient problem and explains in detail the solution to the residual network.
1. The essential reason for the vanishing gradient problem
In a deep neural network, the output of each layer is the combination of the input of the previous layer and It is obtained by multiplying the weight matrix and calculating it through the activation function. As the number of network layers increases, the output of each layer will be affected by the output of previous layers. This means that even small changes in the weight matrix and activation function will have an impact on the output of the entire network. In the backpropagation algorithm, gradients are used to update the weights of the network. The calculation of gradient requires passing the gradient of the next layer to the previous layer through the chain rule. Therefore, the gradients of previous layers will also affect the calculation of gradients. This effect is accumulated when weights are updated and propagated throughout the network during training. Therefore, each layer in a deep neural network is interconnected, and their outputs and gradients influence each other. This requires us to carefully consider the selection of weights and activation functions of each layer, as well as the calculation and transmission methods of gradients when designing and training the network, to ensure that the network can effectively learn and adapt to different tasks and data.
In deep neural networks, when there are many network layers, gradients often "disappear" or "explode". The reason why the gradient disappears is that when the derivative of the activation function is less than 1, the gradient will gradually shrink, causing the gradient of the further layers to become smaller and eventually become unable to be updated, causing the network to be unable to learn. The reason for gradient explosion is that when the derivative of the activation function is greater than 1, the gradient will gradually increase, causing the gradient of the further layers to become larger, eventually causing the network weight to overflow, and also causing the network to be unable to learn.
2. Solution of Residual Network
The residual network solves the problem of gradient disappearance by introducing residual blocks. Between each network layer, the residual block adds the input directly to the output, making it easier for the network to learn the identity mapping. This cross-layer connection design enables gradients to propagate better and effectively alleviates the phenomenon of gradient disappearance. Such a solution can improve the training efficiency and performance of the network.
Specifically, the structure x of the residual block represents the input, F(x) represents the mapping obtained by network learning, and H(x) represents the identity mapping. The output of the residual block is H(x) F(x), which is the input plus the learned mapping.
The advantage of this is that when the network learns an identity mapping, F(x) is 0, and the output of the residual block is equal to the input, that is, H( x) 0=H(x). This avoids the vanishing gradient problem because even if the gradient of F(x) is 0, the gradient of H(x) can still be passed to the previous layer through the cross-layer connection, thus achieving better gradient flow.
In addition, the residual network also uses technologies such as "batch normalization" and "pre-activation" to further enhance the performance and stability of the network. Among them, batch normalization is used to solve the problems of gradient disappearance and gradient explosion, while pre-activation can better introduce nonlinearity and improve the expressive ability of the network.
The above is the detailed content of How do deep residual networks overcome the vanishing gradient problem?. For more information, please follow other related articles on the PHP Chinese website!
 How to Run LLM Locally Using LM Studio? - Analytics VidhyaApr 19, 2025 am 11:38 AM
How to Run LLM Locally Using LM Studio? - Analytics VidhyaApr 19, 2025 am 11:38 AMRunning large language models at home with ease: LM Studio User Guide In recent years, advances in software and hardware have made it possible to run large language models (LLMs) on personal computers. LM Studio is an excellent tool to make this process easy and convenient. This article will dive into how to run LLM locally using LM Studio, covering key steps, potential challenges, and the benefits of having LLM locally. Whether you are a tech enthusiast or are curious about the latest AI technologies, this guide will provide valuable insights and practical tips. Let's get started! Overview Understand the basic requirements for running LLM locally. Set up LM Studi on your computer
 Guy Peri Helps Flavor McCormick's Future Through Data TransformationApr 19, 2025 am 11:35 AM
Guy Peri Helps Flavor McCormick's Future Through Data TransformationApr 19, 2025 am 11:35 AMGuy Peri is McCormick’s Chief Information and Digital Officer. Though only seven months into his role, Peri is rapidly advancing a comprehensive transformation of the company’s digital capabilities. His career-long focus on data and analytics informs
 What is the Chain of Emotion in Prompt Engineering? - Analytics VidhyaApr 19, 2025 am 11:33 AM
What is the Chain of Emotion in Prompt Engineering? - Analytics VidhyaApr 19, 2025 am 11:33 AMIntroduction Artificial intelligence (AI) is evolving to understand not just words, but also emotions, responding with a human touch. This sophisticated interaction is crucial in the rapidly advancing field of AI and natural language processing. Th
 12 Best AI Tools for Data Science Workflow - Analytics VidhyaApr 19, 2025 am 11:31 AM
12 Best AI Tools for Data Science Workflow - Analytics VidhyaApr 19, 2025 am 11:31 AMIntroduction In today's data-centric world, leveraging advanced AI technologies is crucial for businesses seeking a competitive edge and enhanced efficiency. A range of powerful tools empowers data scientists, analysts, and developers to build, depl
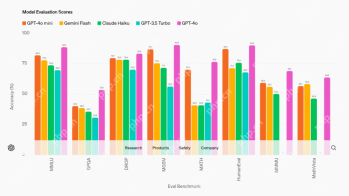 AV Byte: OpenAI's GPT-4o Mini and Other AI InnovationsApr 19, 2025 am 11:30 AM
AV Byte: OpenAI's GPT-4o Mini and Other AI InnovationsApr 19, 2025 am 11:30 AMThis week's AI landscape exploded with groundbreaking releases from industry giants like OpenAI, Mistral AI, NVIDIA, DeepSeek, and Hugging Face. These new models promise increased power, affordability, and accessibility, fueled by advancements in tr
 Perplexity's Android App Is Infested With Security Flaws, Report FindsApr 19, 2025 am 11:24 AM
Perplexity's Android App Is Infested With Security Flaws, Report FindsApr 19, 2025 am 11:24 AMBut the company’s Android app, which offers not only search capabilities but also acts as an AI assistant, is riddled with a host of security issues that could expose its users to data theft, account takeovers and impersonation attacks from malicious
 Everyone's Getting Better At Using AI: Thoughts On Vibe CodingApr 19, 2025 am 11:17 AM
Everyone's Getting Better At Using AI: Thoughts On Vibe CodingApr 19, 2025 am 11:17 AMYou can look at what’s happening in conferences and at trade shows. You can ask engineers what they’re doing, or consult with a CEO. Everywhere you look, things are changing at breakneck speed. Engineers, and Non-Engineers What’s the difference be
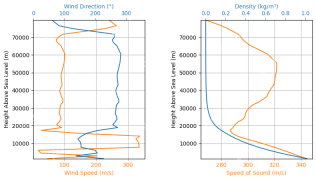 Rocket Launch Simulation and Analysis using RocketPy - Analytics VidhyaApr 19, 2025 am 11:12 AM
Rocket Launch Simulation and Analysis using RocketPy - Analytics VidhyaApr 19, 2025 am 11:12 AMSimulate Rocket Launches with RocketPy: A Comprehensive Guide This article guides you through simulating high-power rocket launches using RocketPy, a powerful Python library. We'll cover everything from defining rocket components to analyzing simula


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Dreamweaver Mac version
Visual web development tools

WebStorm Mac version
Useful JavaScript development tools

Zend Studio 13.0.1
Powerful PHP integrated development environment






