
Univariate linear regression is a supervised learning algorithm used to solve regression problems. It fits the data points in a given dataset using a straight line and uses this model to predict values that are not in the dataset.
Principle of univariate linear regression
The principle of univariate linear regression is to use the relationship between an independent variable and a dependent variable, through Fit a straight line to describe the relationship between them. Through methods such as the least squares method, the sum of squares of the vertical distances from all data points to this fitting straight line is minimized, thereby obtaining the parameters of the regression line, and then predicting the dependent variable value of the new data point.
The general form of the univariate linear regression model is y=ax b, where a is the slope and b is the intercept. Through the least squares method, estimates of a and b can be obtained to minimize the gap between the actual data points and the fitted straight line.
Univariate linear regression has the following advantages: fast operation speed, strong interpretability, and good at discovering linear relationships in data sets. However, when the data is non-linear or there is correlation between features, univariate linear regression may not model and express complex data well.
Simply put, univariate linear regression is a linear regression model with only one independent variable.
Advantages and disadvantages of univariate linear regression
The advantages of univariate linear regression include:
- Fast operation speed: Because the algorithm is simple and conforms to mathematical principles, the modeling and prediction speed of the univariate linear regression algorithm is very fast.
- Very interpretable: Finally, a mathematical function expression can be obtained, and the influence of each variable can be clarified based on the calculated coefficients.
- Good at obtaining linear relationships in data sets.
The disadvantages of univariate linear regression include:
- For nonlinear data or when there is correlation between data features , univariate linear regression can be difficult to model.
- It is difficult to express highly complex data well.
In univariate linear regression, how is the squared error loss function calculated?
In univariate linear regression, we usually use the squared error loss function to measure the prediction error of the model.
The calculation formula of the squared error loss function is:
L(θ0,θ1)=12n∑i=1n(y_i−(θ0 θ1x_i))2
where:
- n is the number of samples
- y_i is the i-th sample Actual values
- θ0 and θ1 are model parameters
- x_i is the independent variable value of the i-th sample
In univariate linear regression , we assume that there is a linear relationship between y and x, that is, y=θ0 θ1x. Therefore, the predicted value can be obtained by substituting the independent variable x into the model, that is, y_pred=θ0 θ1x_i.
The smaller the value of the loss function L, the smaller the prediction error of the model and the better the performance of the model. Therefore, we can get the optimal model parameters by minimizing the loss function.
In the gradient descent method, we gradually approach the optimal solution by iteratively updating the values of parameters. At each iteration, the value of the parameter is updated according to the gradient of the loss function, that is:
θ=θ-α*∂L(θ0,θ1)/∂θ
Among them, α is the learning rate, which controls the change of parameters in each iteration.
Conditions and steps for univariate linear regression using gradient descent method
The conditions for using gradient descent method to perform univariate linear regression include:
1) The objective function is differentiable. In univariate linear regression, the loss function usually uses squared error loss, which is a differentiable function.
2) There is a global minimum. For the squared error loss function, there is a global minimum, which is also a condition for univariate linear regression using gradient descent.
The steps for using gradient descent method to perform univariate linear regression are as follows:
1. Initialize parameters. Choose an initial value, usually 0, as the initial value for the parameter.
2. Calculate the gradient of the loss function. According to the relationship between the loss function and the parameters, the gradient of the loss function with respect to the parameters is calculated. In univariate linear regression, the loss function is usually the squared error loss, and its gradient calculation formula is: θ−y(x)x.
3. Update parameters. According to the gradient descent algorithm, update the value of the parameter, namely: θ=θ−αθ−y(x)x. Among them, α is the learning rate (step size), which controls the change of parameters in each iteration.
4. Repeat steps 2 and 3 until the stopping condition is met. The stopping condition can be that the number of iterations reaches a preset value, the value of the loss function is less than a preset threshold, or other appropriate conditions.
The above steps are the basic process of using the gradient descent method to perform univariate linear regression. It should be noted that the choice of learning rate in the gradient descent algorithm will affect the convergence speed of the algorithm and the quality of the results, so it needs to be adjusted according to the specific situation.
The above is the detailed content of Univariate linear regression. For more information, please follow other related articles on the PHP Chinese website!
 10 Applications of LLM Agents for BusinessApr 13, 2025 am 09:34 AM
10 Applications of LLM Agents for BusinessApr 13, 2025 am 09:34 AMIntroduction Large language models or LLMs are a game-changer especially when it comes to working with content. From supporting summarization, translation, and generation, LLMs like GPT-4, Gemini, and Llama have made it simple
 How LLM Agents are Reshaping Workplace?Apr 13, 2025 am 09:33 AM
How LLM Agents are Reshaping Workplace?Apr 13, 2025 am 09:33 AMIntroduction Large language model (LLM) agents are the latest innovation boosting workplace business efficiency. They automate repetitive activities, boost collaboration, and provide useful insights across departments. Unlike
 Setup Mage AI with PostgresApr 13, 2025 am 09:31 AM
Setup Mage AI with PostgresApr 13, 2025 am 09:31 AMImagine yourself as a data professional tasked with creating an efficient data pipeline to streamline processes and generate real-time information. Sounds challenging, right? That’s where Mage AI comes in to ensure that the lende
 Is Google's Imagen 3 the Future of AI Image Creation?Apr 13, 2025 am 09:29 AM
Is Google's Imagen 3 the Future of AI Image Creation?Apr 13, 2025 am 09:29 AMIntroduction Text-to-image synthesis and image-text contrastive learning are two of the most innovative multimodal learning applications recently gaining popularity. With their innovative applications for creative image creati
 Top 10 YouTube Channels to Learn Excel - Analytics VidhyaApr 13, 2025 am 09:27 AM
Top 10 YouTube Channels to Learn Excel - Analytics VidhyaApr 13, 2025 am 09:27 AMIntroduction Excel is indispensable for boosting productivity and efficiency across all the fields. The wide range of resources on YouTube can help learners of all levels find helpful tutorials specific to their needs. This ar
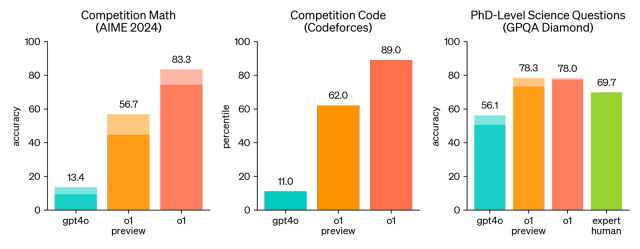 OpenAI o1: A New Model That 'Thinks' Before Answering ProblemsApr 13, 2025 am 09:26 AM
OpenAI o1: A New Model That 'Thinks' Before Answering ProblemsApr 13, 2025 am 09:26 AMHave you heard the big news? OpenAI just rolled out preview of a new series of AI models – OpenAI o1 (also known as Project Strawberry/Q*). These models are special because they spend more time “thinking” befor
 Claude vs Gemini: The Comprehensive Comparison - Analytics VidhyaApr 13, 2025 am 09:20 AM
Claude vs Gemini: The Comprehensive Comparison - Analytics VidhyaApr 13, 2025 am 09:20 AMIntroduction Within the quickly changing field of artificial intelligence, two language models, Claude and Gemini, have become prominent competitors, each providing distinct advantages and skills. Although both models can mana
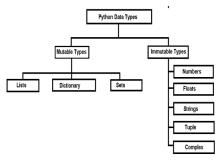 Mutable vs Immutable Objects in Python - Analytics VidhyaApr 13, 2025 am 09:15 AM
Mutable vs Immutable Objects in Python - Analytics VidhyaApr 13, 2025 am 09:15 AMIntroduction Python is an object-oriented programming language (or OOPs).In my previous article, we explored its versatile nature. Due to this, Python offers a wide variety of data types, which can be broadly classified into m


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

SublimeText3 Mac version
God-level code editing software (SublimeText3)






