Deep learning achieves genius-level performance in geometric reasoning. Nature publishes DeepMind's model and receives praise in the Fields Medal winner news

This work represents a breakthrough in AI’s mathematical reasoning capabilities and is an important milestone in the development of general AI systems.

This time, the artificial intelligence algorithm achieved a major breakthrough in the Mathematics Olympiad (IMO).

In the latest issue of the internationally authoritative journal "Nature", a paper was published introducing an artificial intelligence system called AlphaGeometry. The system is able to solve Olympic geometry problems without human demonstration. Experts believe that this is an important milestone in artificial intelligence's progress towards possessing human reasoning capabilities. The publication of this research result is of great significance for promoting the further development of artificial intelligence.

Paper link: https://www.nature.com/articles/s41586-023-06747-5

DeepMind was also published in the paper The code and model were open sourced for a while, GitHub: https://github.com/google-deepmind/alphageometry

This is an artificial intelligence system, from the hands of Google DeepMind researchers , which can solve complex geometric problems at a level close to that of a human Olympiad gold medalist.

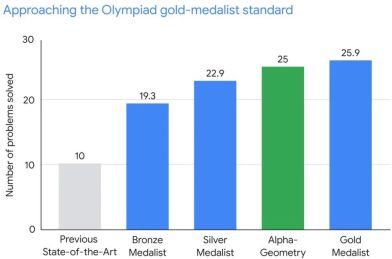
In a benchmark test of 30 Mathematical Olympiad geometry questions, AlphaGeometry solved 25 of the geometry questions within the standard Mathematical Olympiad time limit, while the previous state-of-the-art system only solved 10 of the geometry problems. By comparison, human gold medalists solved an average of 25.9 problems.

# Theorem proving is a challenging task for learning-based AI models. The main reason is that human proofs in most mathematical fields are difficult to translate into machine-verifiable language, thus limiting the amount of data used to train AI models. To overcome this problem, DeepMind proposes an alternative method of using synthetic data for theorem proving. They developed a general guidance framework called AlphaGeometry that has applicability in many fields. By leveraging synthetic data, AlphaGeometry is able to train AI models for theorem proving and produce high-quality results. This method provides an effective solution to the difficulty of theorem proving.

Research Introduction

AlphaGeometry combines language models with "symbolic engines" to perform mathematical inferences with the help of symbols and logical rules. Among them, language models are good at identifying and predicting the subsequent steps of the process, but lack the rigor required for mathematical reasoning; on the other hand, symbolic engines are purely based on formal logic and strict rules, which This enables it to guide the language model toward rational decision-making.

In the research of AlphaGeometry, DeepMind conducted tests from the benchmark test set of 30 Olympic geometry problems (IMO-AG-30) spanning 2000 to 2022. The results showed that AlphaGeometry performed well in competition time Able to solve 25 problems within the limit. The previous state-of-the-art method (Wu’s method) could only solve 10.

It is well known that AI systems often struggle to solve complex problems in geometry and mathematics due to a lack of reasoning skills and training data. The AlphaGeometry system combines the predictive power of neural language models with a rule-constrained inference engine, which work together to find new solutions.

In addition, to solve the data challenge, the study generated a large amount of synthetic training data, namely 100 million examples, in which many theorems have more than 200 steps to prove, which is 4 longer than the average proof length of Mathematical Olympiad theorems. times.

AlphaGeometry demonstrates AI’s growing ability to reason logically and discover and verify new knowledge. Solving Olympic-level geometry problems is an important milestone for AI on the road to more advanced and general artificial intelligence systems.

Ngô Bảo Châu, Fields Medal winner and IMO gold medalist, said: "Now I completely understand why AI researchers first try to solve the geometry problems of the International Mathematical Olympiad (IMO) , because finding their solutions is a bit like playing chess, where we have relatively few reasonable moves at each move. But I'm still shocked that they were able to achieve this. It's an impressive achievement."

^{Wu Baozhu, winner of the 2010 Fields Medal, is currently a professor at the University of Chicago.}

AlphaGeometry is a neuro-symbolic system consisting of a neural language model and a symbolic deduction engine that work together to find proofs of complex geometric theorems. One system provides quick, intuitive ideas, while the other provides more thoughtful, rational decisions.

Because language models are good at identifying general patterns and relationships in data, they can quickly predict potentially useful structures, but often lack rigorous reasoning or interpretation. The symbolic deduction engine, on the other hand, is based on formal logic and uses explicit rules to reach conclusions, which together make up AlphaGeometry.

AlphaGeometry's language model guides its symbolic deduction engine to find possible solutions to geometric problems. General Olympiad geometry problems are based on diagrams and require the addition of new geometric structures to solve, such as points, lines or circles. AlphaGeometry's language model can predict which new structures would be most useful to add out of countless possibilities. These clues help fill in the gaps and allow the symbolic engine to make further inferences about the diagram and get closer to a solution.

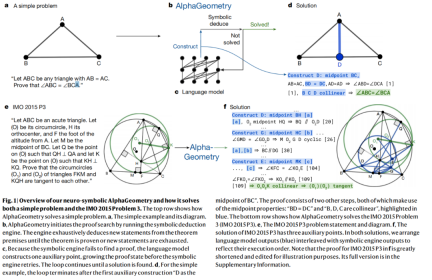
For example, the picture below (top) shows the process of AlphaGeometry solving a simple question. The question is "Let ABC be any triangle with AB = AC. Prove that ∠ABC = ∠BCA."

The AlphaGeometry proof process goes like this: AlphaGeometry starts the proof search by running a symbolic deduction engine. This engine starts from the premises of the theorem and exhaustively derives new statements until the theorem is proved or the new statements are exhausted. If the symbolic engine fails to find a proof, the language model constructs an auxiliary point that adds provable conditions before the symbolic engine restarts. This cycle continues until a solution is found. For the simple example, the loop terminates after the first auxiliary structure "add point D to the midpoint of BC".

The picture below (below) shows AlphaGeometry’s solution to the IMO problem. "Prove that the circumcircles (O1) and (O2) of triangles FKM and KQH are tangent to each other..." AlphaGeometry can also prove such a complex problem, and the proof process also provides auxiliary points, etc. The proof has been greatly shortened and edited for illustrative purposes.

Generate 100 million mathematical reasoning training data

Humans can learn geometry by sketching on paper, examine diagrams, and use modern Have the knowledge to discover new, more complex geometric properties and relationships. This study's approach to generating synthetic data simulates this knowledge-building process at scale. The method for generating synthetic data is shown in Figure 3.

Using highly parallel computing, the system first generates random graphs of 500 million geometric objects and exhaustively derives all relationships between points and lines in each graph. AlphaGeometry finds all the proofs contained in each graph and then works backwards to find out what additional structure, if any, is needed to obtain those proofs. This process is "symbol deduction and retrospection."

^{Visual representation of synthetic data generated by AlphaGeometry}

After that, this huge data pool was Filtering to exclude similar examples resulted in a training dataset of 100 million.

Pioneering Artificial Intelligence Reasoning Capabilities

Every solution provided by AlphaGeometry has been computer checked and verified. The researchers also compared their results with previous artificial intelligence methods and human performance in Olympic competitions. Additionally, math coach and former Olympiad gold medalist Evan Chen evaluates a range of AlphaGeometry solutions for us.

^{Chen Yiting, a PhD candidate in mathematics at MIT, won the IMO 2014 gold medal.}

Evan Chen said: "AlphaGeometry's output is impressive because it is both verifiable and clean. Past artificial intelligence solutions to proof-based competitive problems have sometimes been hit-and-miss ( The output is sometimes correct and requires human checking), while AlphaGeometry does not have this weakness: its solutions have a machine-verifiable structure. On the other hand, its output is still human-readable. One can imagine a coordinate system through brute force A computer program that solves geometry problems: think of pages and pages of tedious algebraic calculations, AlphaGeometry doesn’t do that, it uses the classical rules of geometry with angles and similar triangles like a human student would.”

Recently, financial technology company XTX Markets established the Artificial Intelligence Olympiad Mathematical Prize (AI-MO Prize) to encourage the development of artificial intelligence models that can perform mathematical reasoning. Since each Olympiad has six problems, only two of which typically focus on geometry, AlphaGeometry can only be applied to one-third of the problems in a given Olympiad.

Despite this, AlphaGeometry relied solely on its geometric problem-solving abilities to become the first artificial intelligence model in the world to pass the IMO bronze medal threshold in 2000 and 2015.

DeepMind is already working to advance inference for the next generation of artificial intelligence systems. The researchers believe that given the broad potential of using large-scale synthetic data to train AI systems from scratch, this approach could influence the direction in which future AI systems discover new knowledge in mathematics and other fields.

AlphaGeometry pioneers mathematical reasoning in artificial intelligence—from exploring the beauty of pure mathematics to using language models to solve mathematical and scientific problems. It is hoped that this technology will continue to improve to solve more advanced, abstract mathematical problems.

In addition to mathematics, the impact of AlphaGeometry may also cover more fields including geometric problems, such as computer vision, architecture, and even theoretical physics.

^{Reference content:}

^{https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system -for-geometry/}

The above is the detailed content of Deep learning achieves genius-level performance in geometric reasoning. Nature publishes DeepMind's model and receives praise in the Fields Medal winner news. For more information, please follow other related articles on the PHP Chinese website!