The launch of Mixtral 8x7B has attracted widespread attention in the field of open AI, especially the concept of Mixture-of-Experts (MoEs), which is well known to everyone. The Hybrid Expertise (MoE) concept symbolizes collaborative intelligence and embodies the idea that the whole is greater than the sum of its parts. The MoE model integrates the advantages of multiple expert models to provide more accurate predictions. It consists of a gated network and a set of expert networks, each expert network is good at handling different aspects of a specific task. By properly allocating tasks and weights, the MoE model can take advantage of the expertise of experts, thereby improving the overall prediction performance. This collaborative intelligent model has brought new breakthroughs to the development of the AI field and will play an important role in future applications.
This article will use PyTorch to implement the MoE model. Before introducing the specific code, let’s briefly introduce the architecture of the hybrid expert.
MoE Architecture
MoE consists of two types of networks: (1) expert network and (2) gated network.
Expert Network is a method that uses a proprietary model that performs well on a subset of the data. Its core concept is to cover the problem space through multiple experts with complementary strengths to ensure a comprehensive solution to the problem. Each expert model is trained with unique capabilities and experience, thereby improving overall system performance and effectiveness. Through the use of expert networks, complex tasks and needs can be effectively addressed and better solutions provided.
A gated network is a network used to direct, coordinate, or manage the contributions of experts. It determines which network is best at processing a specific input by learning and weighing the capabilities of different networks for different types of inputs. A well-trained gating network can evaluate new input vectors and assign processing tasks to the most appropriate expert or combination of experts based on their proficiency. The gating network dynamically adjusts weights based on the relevance of the expert's output to the current input to ensure personalized responses. This mechanism of dynamically adjusting weights enables the gating network to flexibly adapt to different situations and needs.

#The above figure shows the processing flow in MoE. The advantage of the mixed expert model is its simplicity. By learning the complex problem space and the reactions of experts while solving the problem, MoE models help produce better solutions than a single expert. The Gating Network acts as an effective manager, assessing scenarios and passing tasks to the best experts. When new data is input, the model can adapt by re-evaluating the expert's strengths against the new input, resulting in a flexible learning approach. In short, the MoE model leverages the knowledge and experience of multiple experts to solve complex problems. Through the management of a gated network, the model can select the most suitable experts to handle tasks according to different scenarios. The advantages of this approach are its ability to produce better solutions than a single expert and its flexibility to adapt to new input data. Overall, the MoE model is an effective and simple method that can be used to solve a variety of complex problems.
MoE provides huge benefits for deploying machine learning models. Here are two notable benefits.
MoE’s core strength lies in its diverse and specialized network of experts. The setting of MoE can handle problems in multiple fields with high accuracy, which is difficult to achieve with a single model.
MoE is inherently scalable. As task complexity increases, more experts can be seamlessly integrated into the system, expanding the scope of expertise without the need to change other expert models. In other words, MoE can package pre-trained experts into machine learning systems to help the systems cope with growing task requirements.
Hybrid expert models have applications in many fields, including recommender systems, language modeling, and various complex prediction tasks. There are rumors that GPT-4 is composed of multiple experts. Although we cannot confirm, a model like gpt-4 will provide the best results by leveraging the power of multiple models through the MoE approach.
Pytorch code
We will not discuss the MOE technology used in large models like Mixtral 8x7B here, but we will write a simple, Custom MOE that can be applied to any task. Through the code, we can understand how MOE works, which is very helpful in understanding how MOE works in large models.
Below we will introduce the code implementation of PyTorch piece by piece.
Import library:
import torch import torch.nn as nn import torch.optim as optim
Define expert model:
class Expert(nn.Module): def __init__(self, input_dim, hidden_dim, output_dim): super(Expert, self).__init__() self.layer1 = nn.Linear(input_dim, hidden_dim) self.layer2 = nn.Linear(hidden_dim, output_dim) def forward(self, x): x = torch.relu(self.layer1(x)) return torch.softmax(self.layer2(x), dim=1)
Here we define an For a simple expert model, you can see that it is a 2-layer mlp, using relu activation, and finally using softmax to output the classification probability.
Define gating model:
# Define the gating model class Gating(nn.Module): def __init__(self, input_dim,num_experts, dropout_rate=0.1): super(Gating, self).__init__() # Layers self.layer1 = nn.Linear(input_dim, 128) self.dropout1 = nn.Dropout(dropout_rate) self.layer2 = nn.Linear(128, 256) self.leaky_relu1 = nn.LeakyReLU() self.dropout2 = nn.Dropout(dropout_rate) self.layer3 = nn.Linear(256, 128) self.leaky_relu2 = nn.LeakyReLU() self.dropout3 = nn.Dropout(dropout_rate) self.layer4 = nn.Linear(128, num_experts) def forward(self, x): x = torch.relu(self.layer1(x)) x = self.dropout1(x) x = self.layer2(x) x = self.leaky_relu1(x) x = self.dropout2(x) x = self.layer3(x) x = self.leaky_relu2(x) x = self.dropout3(x) return torch.softmax(self.layer4(x), dim=1)
门控模型更复杂,有三个线性层和dropout层用于正则化以防止过拟合。它使用ReLU和LeakyReLU激活函数引入非线性。最后一层的输出大小等于专家的数量,并对这些输出应用softmax函数。输出权重,这样可以将专家的输出与之结合。
说明:其实门控网络,或者叫路由网络是MOE中最复杂的部分,因为它涉及到控制输入到那个专家模型,所以门控网络也有很多个设计方案,例如(如果我没记错的话)Mixtral 8x7B 只是取了8个专家中的top2。所以我们这里不详细讨论各种方案,只是介绍其基本原理和代码实现。
完整的MOE模型:
class MoE(nn.Module): def __init__(self, trained_experts): super(MoE, self).__init__() self.experts = nn.ModuleList(trained_experts) num_experts = len(trained_experts) # Assuming all experts have the same input dimension input_dim = trained_experts[0].layer1.in_features self.gating = Gating(input_dim, num_experts) def forward(self, x): # Get the weights from the gating network weights = self.gating(x) # Calculate the expert outputs outputs = torch.stack([expert(x) for expert in self.experts], dim=2) # Adjust the weights tensor shape to match the expert outputs weights = weights.unsqueeze(1).expand_as(outputs) # Multiply the expert outputs with the weights and # sum along the third dimension return torch.sum(outputs * weights, dim=2)
这里主要看前向传播的代码,通过输入计算出权重和每个专家给出输出的预测,最后使用权重将所有专家的结果求和最终得到模型的输出。
这个是不是有点像“集成学习”。
测试
下面我们来对我们的实现做个简单的测试,首先生成一个简单的数据集:
# Generate the dataset num_samples = 5000 input_dim = 4 hidden_dim = 32 # Generate equal numbers of labels 0, 1, and 2 y_data = torch.cat([ torch.zeros(num_samples // 3), torch.ones(num_samples // 3), torch.full((num_samples - 2 * (num_samples // 3),), 2)# Filling the remaining to ensure exact num_samples ]).long() # Biasing the data based on the labels x_data = torch.randn(num_samples, input_dim) for i in range(num_samples): if y_data[i] == 0: x_data[i, 0] += 1# Making x[0] more positive elif y_data[i] == 1: x_data[i, 1] -= 1# Making x[1] more negative elif y_data[i] == 2: x_data[i, 0] -= 1# Making x[0] more negative # Shuffle the data to randomize the order indices = torch.randperm(num_samples) x_data = x_data[indices] y_data = y_data[indices] # Verify the label distribution y_data.bincount() # Shuffle the data to ensure x_data and y_data remain aligned shuffled_indices = torch.randperm(num_samples) x_data = x_data[shuffled_indices] y_data = y_data[shuffled_indices] # Splitting data for training individual experts # Use the first half samples for training individual experts x_train_experts = x_data[:int(num_samples/2)] y_train_experts = y_data[:int(num_samples/2)] mask_expert1 = (y_train_experts == 0) | (y_train_experts == 1) mask_expert2 = (y_train_experts == 1) | (y_train_experts == 2) mask_expert3 = (y_train_experts == 0) | (y_train_experts == 2) # Select an almost equal number of samples for each expert num_samples_per_expert = \ min(mask_expert1.sum(), mask_expert2.sum(), mask_expert3.sum()) x_expert1 = x_train_experts[mask_expert1][:num_samples_per_expert] y_expert1 = y_train_experts[mask_expert1][:num_samples_per_expert] x_expert2 = x_train_experts[mask_expert2][:num_samples_per_expert] y_expert2 = y_train_experts[mask_expert2][:num_samples_per_expert] x_expert3 = x_train_experts[mask_expert3][:num_samples_per_expert] y_expert3 = y_train_experts[mask_expert3][:num_samples_per_expert] # Splitting the next half samples for training MoE model and for testing x_remaining = x_data[int(num_samples/2)+1:] y_remaining = y_data[int(num_samples/2)+1:] split = int(0.8 * len(x_remaining)) x_train_moe = x_remaining[:split] y_train_moe = y_remaining[:split] x_test = x_remaining[split:] y_test = y_remaining[split:] print(x_train_moe.shape,"\n", x_test.shape,"\n", x_expert1.shape,"\n", x_expert2.shape,"\n", x_expert3.shape)
这段代码创建了一个合成数据集,其中包含三个类标签——0、1和2。基于类标签对特征进行操作,从而在数据中引入一些模型可以学习的结构。
数据被分成针对个别专家的训练集、MoE模型和测试集。我们确保专家模型是在一个子集上训练的,这样第一个专家在标签0和1上得到很好的训练,第二个专家在标签1和2上得到更好的训练,第三个专家看到更多的标签2和0。
我们期望的结果是:虽然每个专家对标签0、1和2的分类准确率都不令人满意,但通过结合三位专家的决策,MoE将表现出色。
模型初始化和训练设置:
# Define hidden dimension output_dim = 3 hidden_dim = 32 epochs = 500 learning_rate = 0.001 # Instantiate the experts expert1 = Expert(input_dim, hidden_dim, output_dim) expert2 = Expert(input_dim, hidden_dim, output_dim) expert3 = Expert(input_dim, hidden_dim, output_dim) # Set up loss criterion = nn.CrossEntropyLoss() # Optimizers for experts optimizer_expert1 = optim.Adam(expert1.parameters(), lr=learning_rate) optimizer_expert2 = optim.Adam(expert2.parameters(), lr=learning_rate) optimizer_expert3 = optim.Adam(expert3.parameters(), lr=learning_rate)
实例化了专家模型和MoE模型。定义损失函数来计算训练损失,并为每个模型设置优化器,在训练过程中执行权重更新。
训练的步骤也非常简单
# Training loop for expert 1 for epoch in range(epochs):optimizer_expert1.zero_grad()outputs_expert1 = expert1(x_expert1)loss_expert1 = criterion(outputs_expert1, y_expert1)loss_expert1.backward()optimizer_expert1.step() # Training loop for expert 2 for epoch in range(epochs):optimizer_expert2.zero_grad()outputs_expert2 = expert2(x_expert2)loss_expert2 = criterion(outputs_expert2, y_expert2)loss_expert2.backward()optimizer_expert2.step() # Training loop for expert 3 for epoch in range(epochs):optimizer_expert3.zero_grad()outputs_expert3 = expert3(x_expert3)loss_expert3 = criterion(outputs_expert3, y_expert3)loss_expert3.backward()
每个专家使用基本的训练循环在不同的数据子集上进行单独的训练。循环迭代指定数量的epoch。
下面是我们MOE的训练
# Create the MoE model with the trained experts moe_model = MoE([expert1, expert2, expert3]) # Train the MoE model optimizer_moe = optim.Adam(moe_model.parameters(), lr=learning_rate) for epoch in range(epochs):optimizer_moe.zero_grad()outputs_moe = moe_model(x_train_moe)loss_moe = criterion(outputs_moe, y_train_moe)loss_moe.backward()optimizer_moe.step()
MoE模型是由先前训练过的专家创建的,然后在单独的数据集上进行训练。训练过程类似于单个专家的训练,但现在门控网络的权值在训练过程中更新。
最后我们的评估函数:
# Evaluate all models def evaluate(model, x, y):with torch.no_grad():outputs = model(x)_, predicted = torch.max(outputs, 1)correct = (predicted == y).sum().item()accuracy = correct / len(y)return accuracy
evaluate函数计算模型在给定数据上的精度(x代表样本,y代表预期标签)。准确度计算为正确预测数与预测总数之比。
结果如下:
accuracy_expert1 = evaluate(expert1, x_test, y_test) accuracy_expert2 = evaluate(expert2, x_test, y_test) accuracy_expert3 = evaluate(expert3, x_test, y_test) accuracy_moe = evaluate(moe_model, x_test, y_test) print("Expert 1 Accuracy:", accuracy_expert1) print("Expert 2 Accuracy:", accuracy_expert2) print("Expert 3 Accuracy:", accuracy_expert3) print("Mixture of Experts Accuracy:", accuracy_moe) #Expert 1 Accuracy: 0.466 #Expert 2 Accuracy: 0.496 #Expert 3 Accuracy: 0.378 #Mixture of Experts Accuracy: 0.614
可以看到
专家1正确预测了测试数据集中大约46.6%的样本的类标签。
专家2表现稍好,正确预测率约为49.6%。
专家3在三位专家中准确率最低,正确预测的样本约为37.8%。
而MoE模型显著优于每个专家,总体准确率约为61.4%。
总结
我们测试的输出结果显示了混合专家模型的强大功能。该模型通过门控网络将各个专家模型的优势结合起来,取得了比单个专家模型更高的精度。门控网络有效地学习了如何根据输入数据权衡每个专家的贡献,以产生更准确的预测。混合专家利用了各个模型的不同专业知识,在测试数据集上提供了更好的性能。
同时也说明我们可以在现有的任务上尝试使用MOE来进行测试,也可以得到更好的结果。
The above is the detailed content of Implementing Mixed Expert Model (MoE) using PyTorch. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
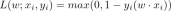 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Dreamweaver Mac version
Visual web development tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.






