 Technology peripherals
Technology peripherals AI
AI Reduce the Transformer rank to improve performance while maintaining LLM without reducing the removal of more than 90% of components in a specific layer
Reduce the Transformer rank to improve performance while maintaining LLM without reducing the removal of more than 90% of components in a specific layerMIT and Microsoft conducted joint research and found that it is possible to improve the task performance of large language models and reduce their size without additional training
In the era of large-scale models, Transformer supports the entire scientific research field with its unique capabilities. Since its introduction, Transformer-based language models (LLM) have demonstrated excellent performance in various tasks. The underlying architecture of Transformer has become the state-of-the-art technology for natural language modeling and reasoning, and has shown strong prospects in fields such as computer vision and reinforcement learning
However, the current Transformer architecture is very large and usually requires a lot of computing resources for training and inference.
Rewrite like this: It makes sense to do this because a Transformer trained with more parameters or data is obviously more capable than other models. However, an increasing number of studies have shown that Transformer-based models and neural networks do not need to retain all adaptation parameters to maintain their learned hypotheses
In general, over-parameterization seems to be very problematic when training models. Helpful, but these models can be heavily pruned before inference. Studies have shown that neural networks can often remove more than 90% of weights without any significant drop in performance. This phenomenon has triggered researchers’ interest in pruning strategies that help model reasoning
Researchers from MIT and Microsoft wrote in the paper "The Truth is in There: Improving Reasoning in Language Models with Layer- Selective Rank Reduction made a surprising finding that careful pruning on specific layers of the Transformer model can significantly improve the performance of the model on certain tasks.

Please click the following link to view the paper: https://arxiv.org/pdf/2312.13558.pdf
-
Paper home page: https://pratyushasharma.github.io/laser/
The study calls this simple intervention LASER (Layer Selective Rank Reduction), The performance of LLM is significantly improved by selectively reducing the high-order components of the learning weight matrix of specific layers in the Transformer model through singular value decomposition. This operation can be performed after the model training is completed without additional parameters or data
During the operation, the reduction of weights is performed in the model-specific weight matrix and layer. The study also found that many similar matrices can be significantly reduced in weight, and typically no performance degradation is observed until more than 90% of the components are removed. The study also found that these reductions can significantly improve accuracy, This finding appears to be not limited to natural language, with performance improvements also found in reinforcement learning.
In addition, this research attempts to infer what is stored in higher-order components so that it can be deleted to improve performance. The study found that LASER answered the correct questions, but before the intervention, the original model mainly responded with high-frequency words (such as "the", "of", etc.), which were not even the same semantic type as the correct answer, and also That is to say, these components will cause the model to generate some irrelevant high-frequency words without intervention.
However, by performing a certain degree of rank reduction, the model's answer can be transformed into correct.
To understand this, the study also explores what the remaining components individually encode, using only their higher-order singular vectors to approximate the weight matrix. It was found that these components described different responses or common high-frequency words in the same semantic category as the correct answer.
These results suggest that when noisy higher-order components are combined with lower-order components, their conflicting responses produce an average answer that may be incorrect. Figure 1 provides a visual representation of the Transformer architecture and the procedure followed by LASER. Here, the weight matrix of a specific layer of multilayer perceptron (MLP) is replaced by its low-rank approximation.
LASER OVERVIEWProvides a detailed introduction to LASER intervention. A single-step LASER intervention is defined by the triplet (τ, ℓ, ρ), which contains the parameter τ, the number of layers ℓ and the reduced rank ρ. Together these values describe the matrices to be replaced by their low-rank approximations, and the degree of approximation. Researchers classify the types of matrices they will intervene on based on parameter types
Researchers focus on matrices in W = {W_q, W_k, W_v, W_o, U_in, U_out}, which consists of MLP and attention layers composed of matrices in . The number of strata represents the stratum of researcher intervention (the first stratum is indexed starting from 0). For example, Llama-2 has 32 layers, so ℓ ∈ {0, 1, 2,・・・31}.
Ultimately, ρ ∈ [0, 1) describes which part of the maximum rank should be preserved when making low-rank approximations. For example, assuming
, the maximum rank of the matrix is d. The researchers replaced it with the ⌊ρ・d⌋- approximation. Figure 1 below is an example of LASER. In this figure, τ = U_in and ℓ = L represent updating the weight matrix of the first layer of MLP in the Transformer block of the L^th layer. Another parameter controls k in the rank-k approximation.
Figure 1 below is an example of LASER. In this figure, τ = U_in and ℓ = L represent updating the weight matrix of the first layer of MLP in the Transformer block of the L^th layer. Another parameter controls k in the rank-k approximation.

LASER can restrict the flow of certain information in a network and unexpectedly yield significant performance benefits. These interventions can also be easily combined, such that a set of interventions can be applied in any order. 
In order to keep the original meaning unchanged, the content needs to be rewritten into Chinese. There is no need to appear the original sentence
In the experimental part, the researcher used the GPT-J model pre-trained on the PILE data set. The number of layers of the model is 27 and the parameters are 6 billion. The model's behavior is then evaluated on the CounterFact dataset, which contains samples of (topic, relation, and answer) triples, with three paraphrase prompts provided for each question. The first is the analysis of the GPT-J model on the CounterFact data set. Figure 2 below shows the impact on the classification loss of the dataset as a result of applying different amounts of rank reduction to each matrix in the Transformer architecture. Each of the Transformer layers consists of a two-layer small MLP, with the input and output matrices shown separately. Different colors represent different percentages of removed components.



The above is the detailed content of Reduce the Transformer rank to improve performance while maintaining LLM without reducing the removal of more than 90% of components in a specific layer. For more information, please follow other related articles on the PHP Chinese website!
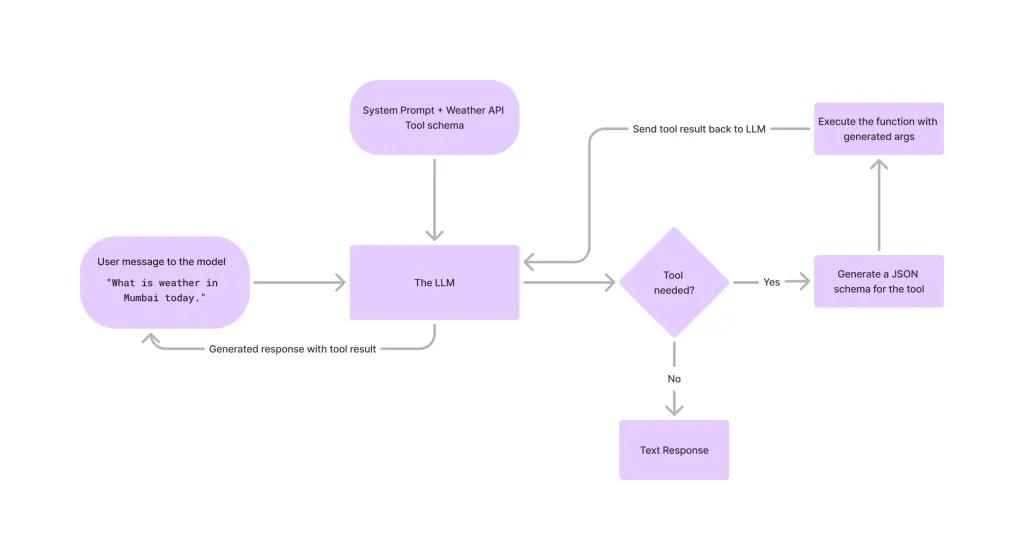 Tool Calling in LLMsApr 14, 2025 am 11:28 AM
Tool Calling in LLMsApr 14, 2025 am 11:28 AMLarge language models (LLMs) have surged in popularity, with the tool-calling feature dramatically expanding their capabilities beyond simple text generation. Now, LLMs can handle complex automation tasks such as dynamic UI creation and autonomous a
 How ADHD Games, Health Tools & AI Chatbots Are Transforming Global HealthApr 14, 2025 am 11:27 AM
How ADHD Games, Health Tools & AI Chatbots Are Transforming Global HealthApr 14, 2025 am 11:27 AMCan a video game ease anxiety, build focus, or support a child with ADHD? As healthcare challenges surge globally — especially among youth — innovators are turning to an unlikely tool: video games. Now one of the world’s largest entertainment indus
 UN Input On AI: Winners, Losers, And OpportunitiesApr 14, 2025 am 11:25 AM
UN Input On AI: Winners, Losers, And OpportunitiesApr 14, 2025 am 11:25 AM“History has shown that while technological progress drives economic growth, it does not on its own ensure equitable income distribution or promote inclusive human development,” writes Rebeca Grynspan, Secretary-General of UNCTAD, in the preamble.
 Learning Negotiation Skills Via Generative AIApr 14, 2025 am 11:23 AM
Learning Negotiation Skills Via Generative AIApr 14, 2025 am 11:23 AMEasy-peasy, use generative AI as your negotiation tutor and sparring partner. Let’s talk about it. This analysis of an innovative AI breakthrough is part of my ongoing Forbes column coverage on the latest in AI, including identifying and explaining
 TED Reveals From OpenAI, Google, Meta Heads To Court, Selfie With MyselfApr 14, 2025 am 11:22 AM
TED Reveals From OpenAI, Google, Meta Heads To Court, Selfie With MyselfApr 14, 2025 am 11:22 AMThe TED2025 Conference, held in Vancouver, wrapped its 36th edition yesterday, April 11. It featured 80 speakers from more than 60 countries, including Sam Altman, Eric Schmidt, and Palmer Luckey. TED’s theme, “humanity reimagined,” was tailor made
 Joseph Stiglitz Warns Of The Looming Inequality Amid AI Monopoly PowerApr 14, 2025 am 11:21 AM
Joseph Stiglitz Warns Of The Looming Inequality Amid AI Monopoly PowerApr 14, 2025 am 11:21 AMJoseph Stiglitz is renowned economist and recipient of the Nobel Prize in Economics in 2001. Stiglitz posits that AI can worsen existing inequalities and consolidated power in the hands of a few dominant corporations, ultimately undermining economic
 What is Graph Database?Apr 14, 2025 am 11:19 AM
What is Graph Database?Apr 14, 2025 am 11:19 AMGraph Databases: Revolutionizing Data Management Through Relationships As data expands and its characteristics evolve across various fields, graph databases are emerging as transformative solutions for managing interconnected data. Unlike traditional
 LLM Routing: Strategies, Techniques, and Python ImplementationApr 14, 2025 am 11:14 AM
LLM Routing: Strategies, Techniques, and Python ImplementationApr 14, 2025 am 11:14 AMLarge Language Model (LLM) Routing: Optimizing Performance Through Intelligent Task Distribution The rapidly evolving landscape of LLMs presents a diverse range of models, each with unique strengths and weaknesses. Some excel at creative content gen


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Dreamweaver Mac version
Visual web development tools

SublimeText3 English version
Recommended: Win version, supports code prompts!

Notepad++7.3.1
Easy-to-use and free code editor

Atom editor mac version download
The most popular open source editor

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.




