ICCV 2023 Oral | How to conduct test segment training in the open world? Self-training method based on dynamic prototype expansion

When promoting the implementation of vision-based perception methods, improving the generalization ability of the model is an important foundation. Test-Time Training/Adaptation (Test-Time Training/Adaptation) enables the model to adapt to the unknown target domain data distribution by adjusting the model parameter weights during the test phase. Existing TTT/TTA methods usually focus on improving the test segment training performance under target domain data in a closed environment. However, in many application scenarios, the target domain is easily affected by strong out-of-domain data (Strong OOD). ), such as semantically irrelevant data categories. In this case, also known as Open World Test Segment Training (OWTTT), existing TTT/TTA usually forcibly classify strong out-of-domain data into known categories, ultimately interfering with weak out-of-domain data (Weak OOD) such as Recognition ability of images disturbed by noise

Recently, South China University of Technology and the A*STAR team proposed the setting of open world test segment training for the first time, and launched corresponding training methods

Paper: https://arxiv.org/abs/2308.09942
The content that needs to be rewritten is: Code link: https: //github.com/Yushu-Li/OWTTT
This article first proposes a strong out-of-domain data sample filtering method with adaptive threshold, which improves the performance of the self-training TTT method in the open world of robustness. The method further proposes a method to characterize strong out-of-domain samples based on dynamically extended prototypes to improve the weak/strong out-of-domain data separation effect. Finally, self-training is constrained by distribution alignment.

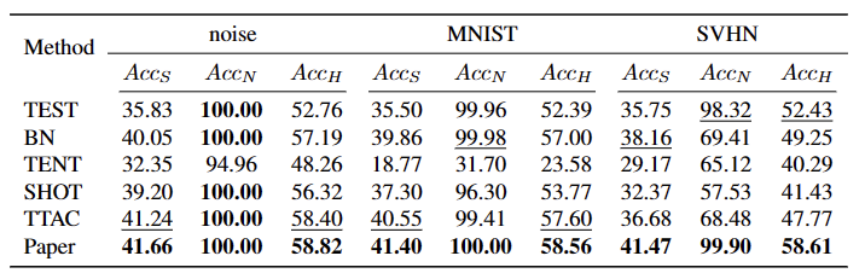
The method in this article achieves optimal performance on 5 different OWTTT benchmarks, and provides a new direction for subsequent research on TTT to explore more robust TTT methods. The research has been accepted as an Oral paper in ICCV 2023.

Introduction

Test segment training (TTT) can access target domain data only during the inference phase and perform on-the-fly inference on test data with distribution shifts. The success of TTT has been demonstrated on a number of artificially selected synthetically corrupted target domain data. However, the capability boundaries of existing TTT methods have not been fully explored.

To promote TTT applications in open scenarios, the focus of research has shifted to investigating scenarios where TTT methods may fail. Many efforts have been made to develop stable and robust TTT methods in more realistic open-world environments. In this work, we delve into a common but overlooked open-world scenario, where the target domain may contain test data distributions drawn from significantly different environments, such as different semantic categories than the source domain, or simply random noise.

We call the above test data strong out-of-distribution data (strong OOD). What is called weak OOD data in this work is test data with distribution shifts, such as common synthetic damage. Therefore, the lack of existing work on this real-life environment motivates us to explore improving the robustness of Open World Test Segment Training (OWTTT), where the test data is contaminated by strong OOD samples

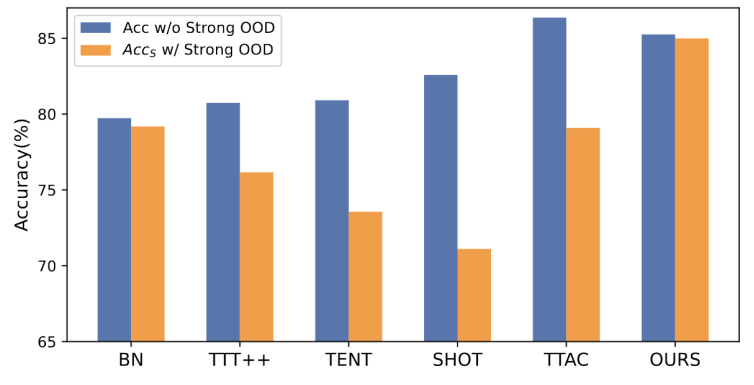
The content that needs to be rewritten is: Figure 1: The results of evaluating the existing TTT method under the OWTTT settingAccording to Figure 1 As shown, we first evaluated the existing TTT methods under the OWTTT setting and found that TTT methods through self-training and distribution alignment will be affected by strong OOD samples. These results indicate that safe test training cannot be achieved by applying existing TTT technology in the open world. We attribute their failure to the following two reasons

Self-training-based TTT has difficulty handling strong OOD samples because it must assign test samples to known classes. Although some low-confidence samples can be filtered out by applying the threshold employed in semi-supervised learning, there is still no guarantee that all strong OOD samples will be filtered out.
Methods based on distribution alignment will be affected when strong OOD samples are calculated to estimate the target domain distribution. Both global distribution alignment [1] and class distribution alignment [2] can be affected and lead to inaccurate feature distribution alignment.
In order to improve the robustness of open-world TTT under the self-training framework, we considered the potential reasons for the failure of existing TTT methods and proposed a solution combining the two technologies

First, we will establish the baseline of TTT on the self-trained variant, that is, clustering in the target domain using the source domain prototype as the cluster center. In order to mitigate the impact of strong OOD on self-training by false pseudo-labels, we propose a hyperparameter-free method to reject strong OOD samples

To further separate the characteristics of weak OOD samples and strong OOD samples, we allow prototypes The pool is expanded by selecting isolated strong OOD samples. Therefore, self-training will allow strong OOD samples to form tight clusters around the newly expanded strong OOD prototype. This will facilitate distribution alignment between source and target domains. We further propose to regularize self-training through global distribution alignment to reduce the risk of confirmation bias

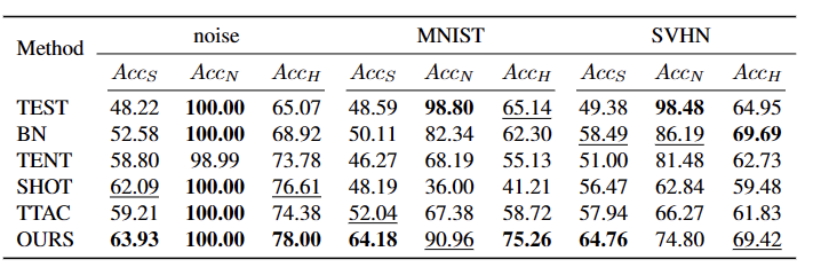
Finally, in order to synthesize the open-world TTT scenario, we use CIFAR10-C, CIFAR100-C, ImageNet-C, VisDA-C, ImageNet-R, Tiny-ImageNet, MNIST and SVHN data sets, and use a data The set is weak OOD, and the others are strong OOD to establish a benchmark data set. We refer to this benchmark as the Open World Test Segment Training Benchmark and hope that this encourages more future work to focus on the robustness of test segment training in more realistic scenarios.

Method

The paper is divided into four parts to introduce the proposed method.

1) Overview of the settings of the training tasks in the test section under the open world.

2) Introduces how to use

Prototype clustering is an unsupervised learning algorithm used to cluster samples in a data set into different categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. These algorithms are widely used in fields such as data mining, pattern recognition, and image processing Implementing TTT and how to extend the prototype for open-world test-time training.

3) Introduces how to use target domain data to

The content that needs to be rewritten is: dynamic prototype extension.

4) Introducing

Distribution Alignment and Prototype Clustering is an unsupervised learning algorithm used to cluster samples in a data set into different categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. These algorithms, widely used in fields such as data mining, pattern recognition, and image processing, are combined to enable powerful open-world test-time training.

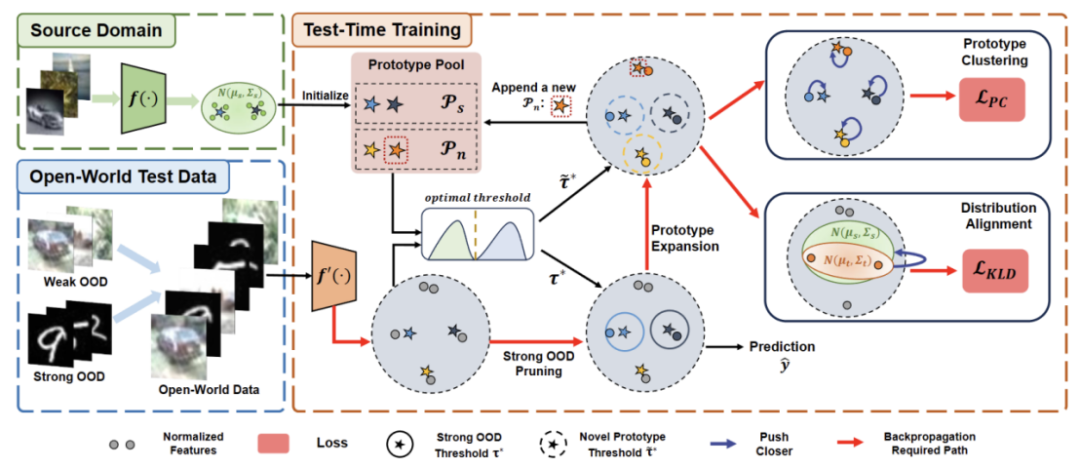
The content that needs to be rewritten is: Figure 2: Method Overview Diagram

Task The goal of setting

TTT is to adapt the source domain pre-trained model to the target domain, where there may be a distribution shift in the target domain relative to the source domain. In standard closed-world TTT, the label spaces of the source and target domains are the same. However, in open-world TTT, the label space of the target domain contains the target space of the source domain, which means that the target domain has unseen new semantic categories

In order to avoid confusion between TTT definitions, we adopt The sequential test time training (sTTT) protocol proposed in TTAC [2] is evaluated. Under the sTTT protocol, test samples are tested sequentially, and model updates are performed after observing small batches of test samples. The prediction for any test sample arriving at timestamp t is not affected by any test sample arriving at t k (whose k is greater than 0).

Prototype clustering is an unsupervised learning algorithm used to cluster samples in a data set into different categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. These algorithms are widely used in fields such as data mining, pattern recognition, and image processing

Inspired by the work using clustering in domain adaptation tasks [3,4], we treat test segment training as discovery Cluster structure in target domain data. By identifying representative prototypes as cluster centers, cluster structures are identified in the target domain and test samples are encouraged to embed near one of the prototypes. Prototype clustering is an unsupervised learning algorithm used to cluster samples in a data set into different categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. The goal of these algorithms, which are widely used in fields such as data mining, pattern recognition, and image processing, is defined as minimizing the negative log-likelihood loss of the cosine similarity between a sample and the cluster center, as shown in the following equation.

We develop a hyperparameter-free method to filter out strong OOD samples to avoid the negative impact of adjusting model weights. Specifically, we define a strong OOD score os for each test sample as the highest similarity to the source domain prototype, as shown in the following equation.

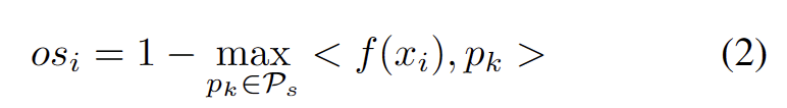
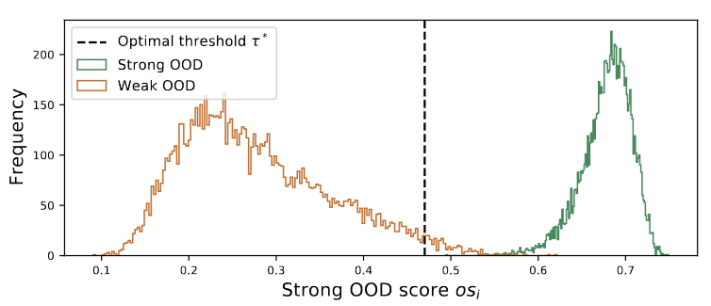
#                                                                                                                                                                                                                                                            The outliers obey a bimodal distribution, as shown in Figure 3. Therefore, instead of specifying a fixed threshold, we define the optimal threshold as the best value that separates the two distributions. Specifically, the problem can be formulated as dividing the outliers into two clusters, and the optimal threshold will minimize the within-cluster variance in . Optimizing the following equation can be efficiently achieved by exhaustively searching all possible thresholds from 0 to 1 in steps of 0.01.

The content that needs to be rewritten is: dynamic prototype extension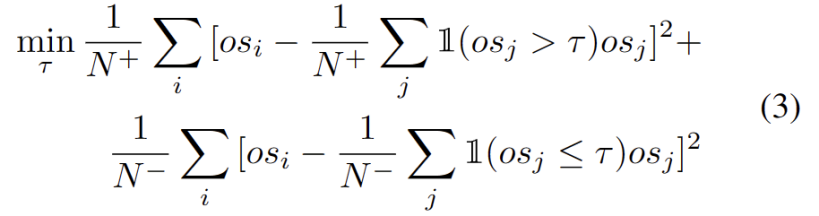

Expanding the strong OOD prototype pool needs to consider both the source domain and the strong OOD prototype to evaluate test samples. To dynamically estimate the number of clusters from data, previous studies have investigated similar problems. The deterministic hard clustering algorithm DP-means [5] was developed by measuring the distance of data points to known cluster centers, and a new cluster is initialized when the distance is above a threshold. DP-means is shown to be equivalent to optimizing the K-means objective, but with an additional penalty on the number of clusters, providing a feasible solution for dynamic prototype extensions that require rewriting.

To alleviate the difficulty of estimating additional hyperparameters, we first define a test sample with an extended strong OOD score as the closest distance to the existing source domain prototype and the strong OOD prototype, as follows. Therefore, testing samples above this threshold will build a new prototype. To avoid adding nearby test samples, we incrementally repeat this prototype expansion process.

With other strong OOD prototypes identified, we define prototypes for test samples. Clustering is an unsupervised learning algorithm for classifying samples in a dataset. clustered into different categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. These algorithms are widely used in fields such as data mining, pattern recognition, and image processing. Loss takes two factors into consideration. First, test samples classified into known classes should be embedded closer to prototypes and farther away from other prototypes, which defines the K-class classification task. Second, test samples classified as strong OOD prototypes should be far away from any source domain prototypes, which defines the K 1 class classification task. With these goals in mind, we prototype clustering, an unsupervised learning algorithm used to cluster samples in a dataset into distinct categories. In prototype clustering, each category is represented by one or more prototypes, which can be samples in the data set or generated according to some rules. The goal of prototype clustering is to achieve clustering by minimizing the distance between samples and the prototypes of the categories to which they belong. Common prototype clustering algorithms include K-means clustering and Gaussian mixture models. These algorithms are widely used in fields such as data mining, pattern recognition, and image processing. The loss is defined as the following formula.

Distribution Alignment Constraints

It is well known that self-training is susceptible to erroneous pseudo-labels. The situation is worsened when the target domain consists of OOD samples. To reduce the risk of failure, we further use distribution alignment [1] as a regularization for self-training, as follows.

Experiments

##We performed experiments on 5 different OWTTT benchmark datasets Tests are conducted including synthetically corrupted datasets and style-varying datasets. The experiment mainly uses three evaluation indicators: weak OOD classification accuracy ACCS, strong OOD classification accuracy ACCN and the harmonic mean of the two ACCH.

Table 1 Performance of different methods on the Cifar10-C data set # Table 2 Different methods of different methods in CIFAR100-C data set

^{# 表 Table 3 Performance of different methods on the ImageNet-C data set}

## Table 4 Performance of different methods on the ImageNet-R data set

#                             Table 5 Performance of different methods on the VisDA-C data set

As shown in the table above, our method has greatly improved compared to the current best methods on almost all data sets, and can effectively identify strong OOD samples and reduce its impact on weak Impact of OOD sample classification. Our method can achieve more robust TTT in open-world scenarios.

When summarizing the content, you need to keep the original meaning unchanged and rewrite the language into ChineseThis article proposes the issues and settings of the Open World Test Segment Training (OWTTT) for the first time , pointed out that existing methods often encounter difficulties in processing target domain data containing strong OOD samples that have semantic offsets from source domain samples, and proposed a rewritten content based on needs: dynamic prototype extended self-training method to solve the above problems. We hope that this work can provide new directions for subsequent research on TTT to explore more robust TTT methods.

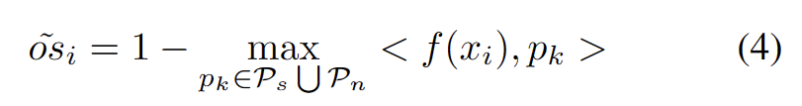
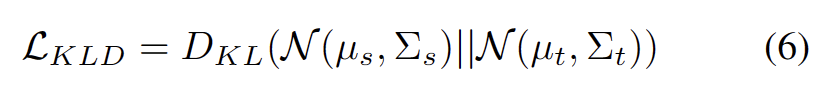
References:

[1] Yuejiang Liu, Parth Kothari, Bastien van Delft, Baptiste Bellot-Gurlet, Taylor Mordan, and Alexandre Alahi. Ttt : When does self-supervised test-time training fail or thrive? In Advances in Neural Information Processing Systems, 2021.

[2] Yongyi Su, Xun Xu, and Kui Jia. Revisiting realistic test-time training: Sequential inference and adaptation by anchored clustering. In Advances in Neural Information Processing Systems, 2022.

[3] Tang Hui and Jia Kui. Discriminative adversarial domain adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, pages 5940-5947, 2020

[4] Kuniaki Saito, Shohei Yamamoto, Yoshitaka Ushiku, and Tatsuya Harada. Open set domain adaptation by backpropagation. In European Conference on Computer Vision, 2018.

[5] Brian Kulis and Michael I Jordan. k-means revisited: a new algorithm via Bayesian nonparametric methods. In International Conference on Machine Learning, 2012

The above is the detailed content of ICCV 2023 Oral | How to conduct test segment training in the open world? Self-training method based on dynamic prototype expansion. For more information, please follow other related articles on the PHP Chinese website!