Transformer is a support vector machine (SVM), a new theory that has triggered discussions in the academic community.
Last weekend, a paper from the University of Pennsylvania and the University of California, Riverside attempted to study the principle of the Transformer structure based on large models. Its optimization geometry in the attention layer is related to the optimal Formal equivalence is established between hard-bound SVM problems where input tokens are separated from non-optimal tokens.
The author stated on hackernews that this theory solves the problem of SVM separating "good" tokens from "bad" tokens in each input sequence. As a token selector with excellent performance, this SVM is essentially different from the traditional SVM that assigns 0-1 labels to the input.
This theory also explains how attention induces sparsity through softmax: "bad" tokens that fall on the wrong side of the SVM decision boundary are suppressed by the softmax function, while "good" tokens fall on the wrong side of the SVM decision boundary. are those tokens that eventually have non-zero softmax probability. It is also worth mentioning that this SVM derives from the exponential properties of softmax.
After the paper was uploaded to arXiv, people expressed their opinions one after another. Some people said: The direction of AI research is really spiraling, is it going to go back again?

After going around in a circle, support vector machines are still not outdated.
Since the publication of the classic paper "Attention is All You Need", the Transformer architecture has brought revolutionary progress to the field of natural language processing (NLP). The attention layer in Transformer accepts a series of input tokens X and evaluates the correlation between tokens by calculating  , where (K, Q) is a trainable key-query parameter, which is ultimately effective Capture remote dependencies.
, where (K, Q) is a trainable key-query parameter, which is ultimately effective Capture remote dependencies.
Now, a new paper called "Transformers as Support Vector Machines" establishes a formal equivalence between self-attentional optimization geometry and the hard-margin SVM problem. , using the outer product linear constraint of token pairs to separate optimal input tokens from non-optimal tokens.

Paper link: https://arxiv.org/pdf/2308.16898.pdf
This This formal equivalence is based on the paper "Max-Margin Token Selection in Attention Mechanism" by Davoud Ataee Tarzanagh et al., which can describe the implicit bias of a 1-layer transformer optimized through gradient descent:
(1) Optimize the attention layer parameterized by (K, Q), and converge to an SVM solution through vanishing regularization, which minimizes the combined parameters # The nuclear norm of  ##. In contrast, parameterizing directly via W minimizes the Frobenius norm SVM objective. The paper describes this convergence and emphasizes that it can occur in the direction of a local optimum rather than a global optimum.
##. In contrast, parameterizing directly via W minimizes the Frobenius norm SVM objective. The paper describes this convergence and emphasizes that it can occur in the direction of a local optimum rather than a global optimum.
(2) The paper also demonstrates the local/global directional convergence of W parameterization gradient descent under appropriate geometric conditions. Importantly, overparameterization catalyzes global convergence by ensuring the feasibility of the SVM problem and ensuring a benign optimization environment without stationary points.
(3) Although the theory of this study mainly applies to linear prediction heads, the research team proposed a more general SVM equivalent that can predict 1 with non-linear heads/MLP Implicit bias of layer transformer.
Overall, the results of this study are applicable to general data sets and can be extended to cross-attention layers, and the practical validity of the study conclusions has been obtained through thorough numerical experiments verify. This study establishes a new research perspective that views multi-layer transformers as SVM hierarchies that separate and select the best tokens.
Specifically, given an input sequence of length T and embedding dimension d  , this study analyzes core cross-attention and self-attention Model:
, this study analyzes core cross-attention and self-attention Model:

Among them, K, Q, and V are trainable key, query, and value matrices respectively,  ; S (・) represents softmax nonlinearity, which is applied row by row. The study assumes that the first token of Z (denoted by z) is used for prediction. Specifically, given a training data set
; S (・) represents softmax nonlinearity, which is applied row by row. The study assumes that the first token of Z (denoted by z) is used for prediction. Specifically, given a training data set  ,
,  ,
,  , the study uses a decreasing loss function
, the study uses a decreasing loss function  Minimize:
Minimize: 
 Here, h (・):
Here, h (・):
is the included value weight Predictive header for V. In this formulation, the model f (・) accurately represents a single-layer transformer where the attention layer is followed by an MLP. The author restores the self-attention in (2) by setting  , where x_i represents the first token of the sequence X_i. Due to the nonlinear nature of the softmax operation, it poses a huge challenge to optimization. Even if the prediction head is fixed and linear, the problem is non-convex and non-linear. In this study, the authors focus on optimizing attention weights (K, Q, or W) and overcoming these challenges to establish the basic equivalence of SVMs.
, where x_i represents the first token of the sequence X_i. Due to the nonlinear nature of the softmax operation, it poses a huge challenge to optimization. Even if the prediction head is fixed and linear, the problem is non-convex and non-linear. In this study, the authors focus on optimizing attention weights (K, Q, or W) and overcoming these challenges to establish the basic equivalence of SVMs.  The structure of the paper is as follows: Chapter 2 introduces the preliminary knowledge of self-attention and optimization; Chapter 3 analyzes the optimization geometry of self-attention, showing that the attention parameter RP converges to the maximum Marginal solution; Chapters 4 and 5 introduce the global and local gradient descent analysis respectively, showing that the key-query variable W converges to the solution of (Att-SVM); Chapter 6 provides the solution on the nonlinear prediction head and generalized SVM Results in terms of equivalence; Chapter 7 extends the theory to sequential and causal predictions; Chapter 8 discusses related literature. Finally, Chapter 9 concludes by proposing open questions and future research directions.
The structure of the paper is as follows: Chapter 2 introduces the preliminary knowledge of self-attention and optimization; Chapter 3 analyzes the optimization geometry of self-attention, showing that the attention parameter RP converges to the maximum Marginal solution; Chapters 4 and 5 introduce the global and local gradient descent analysis respectively, showing that the key-query variable W converges to the solution of (Att-SVM); Chapter 6 provides the solution on the nonlinear prediction head and generalized SVM Results in terms of equivalence; Chapter 7 extends the theory to sequential and causal predictions; Chapter 8 discusses related literature. Finally, Chapter 9 concludes by proposing open questions and future research directions.
The main contents of the paper are as follows:
Implicit bias in the attention layer (Chapter 2-3)
Optimizing the attention parameters (K, Q) when regularization disappears will converge in the direction to the maximum marginal solution of
, whose kernel The norm target is the combined parameter  . In the case where the cross-attention is directly parameterized with the combined parameter W, the regularization path (RP) directionally converges to the (Att-SVM) solution targeting the Frobenius norm.
. In the case where the cross-attention is directly parameterized with the combined parameter W, the regularization path (RP) directionally converges to the (Att-SVM) solution targeting the Frobenius norm.  This is the first result to formally distinguish between W and (K, Q) parametric optimization dynamics, revealing low-order biases in the latter. The theory of this study clearly describes the optimality of selected tokens and naturally extends to sequence-to-sequence or causal classification settings.
This is the first result to formally distinguish between W and (K, Q) parametric optimization dynamics, revealing low-order biases in the latter. The theory of this study clearly describes the optimality of selected tokens and naturally extends to sequence-to-sequence or causal classification settings.
Convergence of Gradient Descent (Chapter 4-5)
With proper initialization and linear head h (・), the gradient descent (GD) iteration of the combined key-query variable W converges in the direction to the local optimal solution of (Att-SVM) (Section 5). To achieve a local optimum, the selected token must have a higher score than adjacent tokens.
The local optimal direction is not necessarily unique and can be determined based on the geometric characteristics of the problem [TLZO23]. As an important contribution, the authors identify geometric conditions that guarantee convergence toward the global optimum (Chapter 4). These conditions include:
- The best token has a significant difference in score;
- The initial gradient direction is consistent with the best token.
In addition, the paper also shows the feasibility of over-parameterization (ie, the dimension d is large, and the same conditions) by ensuring (1) (Att-SVM) , and (2) a benign optimization landscape (that is, there are no stationary points and false local optimal directions) to catalyze global convergence (see Section 5.2).
Figures 1 and 2 illustrate this.


#Generality of SVM equivalence (Chapter 6)
When optimizing with linear h (・), the attention layer is inherently biased from Select a token in each sequence (also known as hard attention). This is reflected in (Att-SVM), where the output token is a convex combination of the input tokens. In contrast, the authors show that nonlinear heads must be composed of multiple tokens, thus highlighting their importance in transformer dynamics (Section 6.1). Using insights gained from theory, the authors propose a more general SVM equivalent approach.
It is worth noting that they prove that in general cases not covered by the theory (for example, h (・) is an MLP), the method in this paper can accurately predict the gradient descent training Implicit biases in attention. Specifically, our general formula decouples the attention weight into two parts: a directional part controlled by SVM, which selects markers by applying a 0-1 mask; and a finite part, which adjusts the softmax Probability determines the precise composition of the selected token.
An important feature of these findings is that they apply to arbitrary data sets (as long as SVM is feasible) and can be verified numerically. The authors extensively experimentally verified the maximum marginal equivalence and implicit bias of the transformer. The authors believe that these findings contribute to the understanding of transformers as a hierarchical maximum-margin token selection mechanism and can lay the foundation for upcoming research on their optimization and generalization dynamics.
The above is the detailed content of Listen to me, Transformer is a support vector machine. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
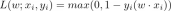 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Dreamweaver Mac version
Visual web development tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.





