
If you have ever used C, you must know what subarrays are and how useful they are. As we all know that in C we can solve multiple mathematical problems easily. So, in this article, we will explain how to find the complete information of M odd numbers in C with the help of these subarrays.
In this problem, we need to find a number of subarrays consisting of a given array and integers m, where each subarray contains exactly m odd numbers. Here is a simple example of this approach -
Input : array = { 6,3,5,8,9 }, m = 2
Output : 5
Explanation : Subarrays with exactly 2 odd numbers are
{ 3,5 }, { 6,3,5 }, { 3,5,8 }, { 5,8,9 }, { 6,3,5,8 }, { 3,5,8,9 }
Input : array = { 1,6,3,2,5,4 }, m = 2
Output : 6
Explanation : Subarrays with exactly 2 odd numbers are
{ 1,6,3 }, { 3,2,5 }, { 1,6,3,2 }, { 6,3,2,5 }, { 3,2,5,4 }, { 6,3,2,5,4 }First approach
In this approach all possible sub-arrays are generated from the given array and each sub-array is checked Whether the array has exactly m odd numbers. This is a simple generation and lookup method with a time complexity of O(n2).
Example
#include <bits/stdc++.h>
using namespace std;
int main (){
int a[] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0; // n is size of array, m numbers to be find in subarrays,
// count is number of subarray with m odd numbers
for (int i = 0; i < n; i++){ // outer loop to process each element.
int odd = 0;
for (int j = i; j < n; j++) {// inner loop to find subarray with m number
if (a[j] % 2)
odd++;
if (odd == m) // if odd numbers become equals to m.
count++;
}
}
cout << "Number of subarrays with n numbers are: " << count;
return 0;
}Output
Number of subarrays with n numbers are: 6
Description of the above code
In this code, we use nested loops to find m odd subarrays , the outer loop is used to increment "i", which will be used to process each element in the array.
The inner loop is used to find subarrays and process elements until the odd counter reaches m, increment the result counter count for each subarray found, and finally print the result stored in the count
Second One approach
Another approach is to create an array to store the "i" number of odd prefixes, process each element, and increment the number of odd numbers each time an odd number is found.
When the number of odd numbers exceeds or equals m, add the number at the (odd - m) position in the prefix array to it.
When the odd number becomes greater than or equal to m, we count the number of subarrays formed until the index and "odd - m" numbers are added to the count variable. After each element is processed, the result is stored in the count variable.
Example
#include <bits/stdc++.h>
using namespace std;
int main (){
int array[ ] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0, odd = 0, i;
int prefix_array[n + 1] = { 0 };
// outer loop to process every element of array
for (i = 0; i < n; i++){
prefix_array[odd] = prefix_array[odd] + 1; // implementing value at odd index in prefix_array[ ]
// if array element is odd then increment odd variable
if (array[i] % 2 == 0)
odd++;
// if Number of odd element becomes equal or greater than m
// then find the number of possible subarrays that can be formed till the index.
if (odd >= m)
count += prefix_array[odd - m];
}
cout << "Number of subarrays with n numbers are: " << count;
return 0;
}Output
Number of subarrays with n numbers are: 6
Explanation of the above code
Initialize arrays and variables with starting values -
int array[ 6 ] = { 1, 6, 3, 2, 5, 4 };
int n = 6, m = 2, count = 0, odd = 0, i;
int prefix_array[n + 1] = { 0 };Here , we initialize the variable n with the size of the array, m with the number of odd numbers to find, the count with 0 to keep a count of possible subarrays, the odd numbers with 0, and the variable n 0 with a prefix_array of size n 1 .
Understanding Loops
for (i = 0; i < n; i++){
prefix_array[odd] = prefix_array[odd] + 1;
if (array[i] % 2 == 0)
odd++;
if (odd >= m)
count += prefix_array[odd - m];
}In this loop we implement the value at odd index in prefix_array[] and then increment the odd variable if an odd number is found. We find that when odd variables are equal to or greater than m, the number of subarrays can be formed, up to index.
Finally, we print the m odd subarray numbers stored in the count variable and get the output.
Conclusion
In this article, we learned about the method of finding the number of m odd subarrays through two methods-
Generate each sub-array array and check if there are m odd numbers in it and increment the count for each sub-array found. The time complexity of this code is O(n2).
Efficient way, iterate through each element of the array and create a prefix array, then use the help of prefix array. The time complexity of this code is O(n).
Hope this article helps you understand the problem and solution.
The above is the detailed content of Programming in C++, find the number of subarrays with m odd numbers. For more information, please follow other related articles on the PHP Chinese website!
 使用C++编写代码,找到第N个非平方数Aug 30, 2023 pm 10:41 PM
使用C++编写代码,找到第N个非平方数Aug 30, 2023 pm 10:41 PM我们都知道不是任何数字的平方的数字,如2、3、5、7、8等。非平方数有N个,不可能知道每个数字。因此,在本文中,我们将解释有关无平方数或非平方数的所有内容,以及在C++中查找第N个非平方数的方法。第N个非平方数如果一个数是整数的平方,则该数被称为完全平方数。完全平方数的一些例子是-1issquareof14issquareof29issquareof316issquareof425issquareof5如果一个数不是任何整数的平方,则该数被称为非平方数。例如,前15个非平方数是-2,3,5,6,
 使用C++编写的数组右旋转的反转算法Sep 08, 2023 pm 08:17 PM
使用C++编写的数组右旋转的反转算法Sep 08, 2023 pm 08:17 PM在本文中,我们将了解逆转算法,将给定的数组向右旋转k个元素,例如−Input:arr[]={4,6,2,6,43,7,3,7},k=4Output:{43,7,3,7,4,6,2,6}Explanation:Rotatingeachelementofarrayby4-elementtotherightgives{43,7,3,7,4,6,2,6}.Input:arr[]={8,5,8,2,1,4,9,3},k=3Output:{4,9,3,8,5,8,2,1}寻找解决方案的方
 在C编程中,找到一个圆的面积Aug 25, 2023 pm 10:57 PM
在C编程中,找到一个圆的面积Aug 25, 2023 pm 10:57 PM圆是封闭图形。圆上的所有点到圆内一点的距离都相等。中心点称为圆心。点到圆心的距离称为半径。面积是封闭图形尺寸跨度的定量表示。圆的面积是圆的尺寸内包围的面积。计算圆面积的公式,Area=π*r*r为了计算面积,我们给出了圆的半径作为输入,我们将使用公式来计算面积,算法STEP1:Takeradiusasinputfromtheuserusingstdinput.STEP2:Calculatetheareaofcircleusing, area=(
 使用C++找到数组中唯一配对的数量Sep 07, 2023 am 11:53 AM
使用C++找到数组中唯一配对的数量Sep 07, 2023 am 11:53 AM我们需要适当的知识才能在C++的数组语法中创建几个唯一的对。在查找唯一对的数量时,我们计算给定数组中的所有唯一对,即可以形成所有可能的对,其中每个对应该是唯一的。例如-Input:array[]={5,5,9}Output:4Explanation:Thenumberofalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[]={5,4,3,2,2}Output:16寻找解决方案的方法有两种方法可以解决这个问题,它们是−
 使用C++编写代码,找到具有相同最小值和最大值的子数组的数量Aug 25, 2023 pm 11:33 PM
使用C++编写代码,找到具有相同最小值和最大值的子数组的数量Aug 25, 2023 pm 11:33 PM在本文中,我们将使用C++解决寻找最大值和最小值相同的子数组数量的问题。以下是该问题的示例−Input:array={2,3,6,6,2,4,4,4}Output:12Explanation:{2},{3},{6},{6},{2},{4},{4},{4},{6,6},{4,4},{4,4}and{4,4,4}arethesubarrayswhichcanbeformedwithmaximumandminimumelementsame.Input:array={3,3,1,5,
 使用C++按给定大小将双向链表分组反转Sep 04, 2023 am 09:49 AM
使用C++按给定大小将双向链表分组反转Sep 04, 2023 am 09:49 AM在这个问题中,我们得到一个指向链表头部的指针和一个整数k。在大小为k的组中,我们需要反转链表。例如-Input:1<->2<->3<->4<->5(doublylinkedlist),k=3Output:3<->2<->1<->5<->4寻找解决方案的方法在这个问题中,我们将制定一个递归算法来解决这个问题。在这种方法中,我们将使用递归并使用递归来解决问题。示例#include<iostream&
 使用C++编写的数组旋转的逆转算法Aug 28, 2023 pm 11:13 PM
使用C++编写的数组旋转的逆转算法Aug 28, 2023 pm 11:13 PM在给定的问题中,我们有一个数组,并且我们需要使用反转算法将数组旋转d个元素,例如−Input:arr[]=[1,2,3,4,5,6,7],d=2Output:arr[]=[3,4,5,6,7,1,2]Explanation:Asyoucanseewehavetorotatethisarraybyd=2butourmaintaskistoachievethisbyusingareversaltechnique.我们对数组的旋转进行了一些反转技术的计算,并得出结论:首先,我们反转
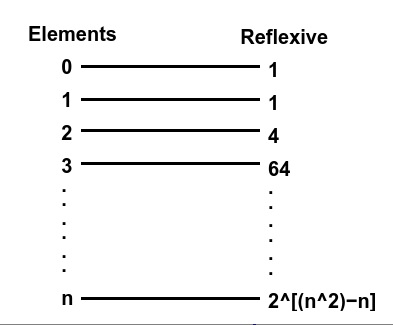 使用C++编写,找到一个集合上的自反关系的数量Aug 26, 2023 pm 08:17 PM
使用C++编写,找到一个集合上的自反关系的数量Aug 26, 2023 pm 08:17 PM在本文中,我们将解释在一个集合上找到反身关系的方法。在这个问题中,我们给出一个数字n,以及一个由n个自然数组成的集合,我们必须确定反身关系的数量。反身关系-如果对于集合A中的每个'a',(a,a)属于关系R,则称关系R是集合A上的反身关系。例如-Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

WebStorm Mac version
Useful JavaScript development tools

Atom editor mac version download
The most popular open source editor

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment







