 Backend Development
Backend Development C++
C++ Written in C++, find the number of triangles formed by a set of points on three lines
Written in C++, find the number of triangles formed by a set of points on three lines
Now we have several points present in the 3 rows; for example, we need to find out how many triangles these points can form
Input: m = 3, n = 4, k = 5 Output: 205 Input: m = 2, n = 2, k = 1 Output: 10
We will apply some combinations Mathematics to solve this problem and formulate some formulas to solve this problem.
Method to find solutions
In this method we will devise a formula: applying combinatorics to the current situation, this formula will provide us with the result.
C code for the above method
This is the C syntax we can use as input to solve the given problem -
Example
#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
long long fact(long long n) {
if(n <= 1)
return 1;
return ((n % MOD) * (fact(n-1) % MOD)) % MOD;
}
long long comb(int n, int r) {
return (((fact(n)) % MOD) / ((fact(r) % MOD) * (fact(n-r) % MOD)) % MOD);
}
int main() {
int n = 3;
int m = 4;
int r = 5;
long long linen = comb(n, 3); // the combination of n with 3.
long long linem = comb(m, 3); // the combination of m with 3.
long long liner = comb(r, 3); //the combination of r with 3.
long long answer = comb(n + m + r, 3); // all possible comb of n, m , r with 3.
answer -= (linen + linem + liner);
cout << answer << "\n";
return 0;
}Output
205
Explanation of the above code
In this method, we find all possible combinations of n m r and three numbers, that is, comb(n m r, 3). Now, you know that the condition for three points to become a triangle is that they cannot be collinear, so we find all possible collinear points obtained by summing the combinations of n, m, r, and then combine this sum with n m r By subtracting the changes in the three numbers, we get the answer and print it out.
Conclusion
This article discusses how to calculate how many triangles can be formed from a set of points on three lines by applying combinatorics. We also learned the C program and complete method (normal method) to solve this problem. We can write the same program in other languages like C, Java, Python and others. Hope this article is helpful to you.
The above is the detailed content of Written in C++, find the number of triangles formed by a set of points on three lines. For more information, please follow other related articles on the PHP Chinese website!
 使用C++编写,找出由三条线上的一组点组成的三角形的数量Sep 09, 2023 am 09:53 AM
使用C++编写,找出由三条线上的一组点组成的三角形的数量Sep 09, 2023 am 09:53 AM现在我们得到了3行中存在的几个点;例如,我们需要找出这些点可以形成多少个三角形Input:m=3,n=4,k=5Output:205Input:m=2,n=2,k=1Output:10我们将应用一些组合数学来解决这个问题,并制定一些公式来解决这个问题。寻找解决方案的方法在这种方法中,我们将设计一个公式:将组合学应用于当前情况,这个公式将为我们提供结果。上述方法的C++代码这是我们可以用作求解的输入的C++语法给定的问题-示例#include<bits/stdc++.h>#define
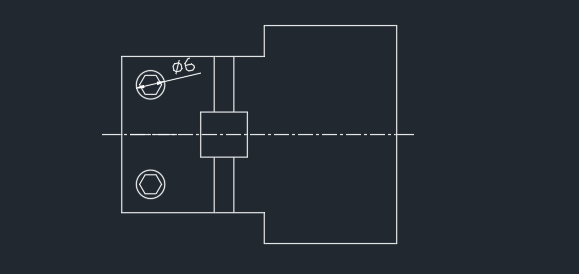 cad如何把线打断成几等分Feb 27, 2024 am 11:40 AM
cad如何把线打断成几等分Feb 27, 2024 am 11:40 AM在CAD设计过程中,我们经常需要将某条直线或曲线分割成几等分。这种需求在多种场景中都极为常见,如工程绘图、产品设计、城市规划等。例如,当需要在特定距离内均匀地布置灯柱,或在产品侧面上等距地设置螺丝时,等分分割功能就显得尤为重要。为了满足这种精确的分割需求,CAD软件为我们提供了多种工具和方法。那么究竟该如何打断线路呢,这篇教程攻略就将为大家带来详细的内容介绍,想要了解的用户们就快来下文中一起学习一下吧!cad把线打断成几等分方法分享1、打开CAD2023软件,创建CAD图形。如下图:2、点击修改
 “丶”这个点用键盘怎么打出来?Feb 15, 2024 pm 01:51 PM
“丶”这个点用键盘怎么打出来?Feb 15, 2024 pm 01:51 PM在使用键盘的打字的时候会有很多的用户比较好奇“丶”这个点用键盘是怎么打出来的?那么下面就来看一下小编给大家带来的键盘上打出这个“丶”符号的方法吧。一、“丶”点用键盘打出打出直接输入【dian】在选择栏上就会看到【丶】的标点符号。二、特殊符号在搜狗拼音输入法中,当切换至中文状态后,按下v键会出现一些特殊的符号。这些符号包括数字(如:v123)、日期(如:v2013/1/1)、算式(如:v1+1)和函数(如:v2~3)。这些符号可以方便地输入各种不同的信息。2.接着再按下数字键,0到9随便一个都可以
 如何在Java中检查三个点是否共线?Sep 05, 2023 pm 06:41 PM
如何在Java中检查三个点是否共线?Sep 05, 2023 pm 06:41 PM如果三个点都位于一条直线上,则称这三个点共线。如果这些点不在同一条直线上,则它们不是共线点。这意味着如果三个点(x1,y1),(x2,y2),(x3,y3)在同一条直线上,则它们是共线的。其中,x1、y1、x2、y2、x3、y3是x轴和y轴上的点,(x1,y1)、(x2,y2)、(x3,y3)是坐标。数学上,有两种方法可以确定三个点是否共线。通过使用点求三角形的面积,如果三角形的面积为零,则三个点共线。Formulatofindareaoftriangle=0。5*[x1*(y2-y3)+x2*
 安钛克650电源主板线接口的引脚数量是多少?(安钛克650电源接线图)Jan 03, 2024 am 10:46 AM
安钛克650电源主板线接口的引脚数量是多少?(安钛克650电源接线图)Jan 03, 2024 am 10:46 AM安钛克650w主板线是几pin的安钛克650W电源主板的电源线通常是24pin的,这是主板上最大的电源接口。它的作用是连接主板和电源,为主板和其他系统组件提供电源。此外,安钛克650W电源还可能包含其他类型的电源接口,如CPU8pin、PCIe6+2pin等,用于连接CPU和独立显卡等其他组件。主板走线教程主板走线是指在设计主板时,将各个电子元件之间的电路连接起来的过程。在这个过程中,需要考虑电路的稳定性、信号传输的速度和准确性等因素。根据电路图进行走线时,需注意布局和选择合适的线宽和距离,避免
 如何在Java中找到一条线的中点?Sep 02, 2023 pm 06:45 PM
如何在Java中找到一条线的中点?Sep 02, 2023 pm 06:45 PM假设(x1,y1)是线的起点,(x2,y2)是线的终点。要获得直线的中点,我们必须使用直线的中点公式。Midpoint=((x1+x2)/2,(y1+y2)/2)在本文中,我们将看到如何使用Java编程语言找到线段的中点,当线段的两个点已知时。展示给你一些实例实例1假设这两个点是(2,3)和(3,5)通过使用线段的中点公式,a=(x1+x2)/2=(2+3)/2=2.5b=(y1+y2)/2=(3+5)/2=4.0因此,直线的中点是(2.5,4.0)实例2假设这两个点是(2,-3)和(-3,5)
 通过一个点的最大不同直线数在C中Aug 26, 2023 am 10:25 AM
通过一个点的最大不同直线数在C中Aug 26, 2023 am 10:25 AM我们得到每条线的数字N和两个点(x1,y1)和(x2,y2)的坐标。目标是从给定的直线中找到可以穿过单个点的最大直线数,使得没有两条直线相互覆盖,并且不执行旋转。我们将把直线表示为(对)m,c)其中y=mx+c,m是斜率m=y2-y1/x2-x1给定c1!=c2,具有相同m的线是平行的。我们将计算不同的坡度(米)。对于垂直线,如果x1=x2,则斜率=INT_MAX,否则为m。让我们通过示例来理解。输入 Line1(x1,y1)=(4,10)(x2,y2)=(2,2)Line2(x1,y1)=(2
 使用C++编写,找到N叉树中给定节点的兄弟节点数量Aug 26, 2023 pm 08:33 PM
使用C++编写,找到N叉树中给定节点的兄弟节点数量Aug 26, 2023 pm 08:33 PM在本文中,我们将提供完整的信息来确定n叉树中给定节点的兄弟节点数量。我们需要使用用户给定的key值找到该节点的兄弟节点;如果不是,则输出-1。我们只能使用一种方法-简单方法在这种方法中,我们将遍历所有节点并检查子节点是否与用户具有相同的值。如果存在,我们回答子节点的数量-1(给定值)。示例#include<bits/stdc++.h>usingnamespacestd;classNode{ //structureofnodesofourtree.public:&am


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

WebStorm Mac version
Useful JavaScript development tools

SublimeText3 Linux new version
SublimeText3 Linux latest version






