Home >Technology peripherals >AI >Deep Thinking | Where is the capability boundary of large models?
Deep Thinking | Where is the capability boundary of large models?
- PHPzforward
- 2023-09-08 17:41:051374browse
If we have infinite resources, such as infinite data, infinite computing power, infinite models, perfect optimization algorithms and generalization performance, can the resulting pre-trained model be used to solve all problems? ?
This is a question that everyone is very concerned about, but existing machine learning theories cannot answer it. It has nothing to do with the expressive ability theory, because the model is infinite and the expressive ability is naturally infinite. It is also irrelevant to optimization and generalization theory, because we assume that the optimization and generalization performance of the algorithm are perfect. In other words, the problems of previous theoretical research no longer exist here!
Today, I will introduce to you the paper On the Power of Foundation Models I published at ICML'2023, and give an answer from the perspective of category theory.
What is category theory?
If you are not a mathematics major, you may be unfamiliar with category theory. Category theory is called the mathematics of mathematics and provides a basic language for modern mathematics. Almost all modern mathematical fields are described in the language of category theory, such as algebraic topology, algebraic geometry, algebraic graph theory, etc. Category theory is the study of structure and relationships. It can be seen as a natural extension of set theory: in set theory, a set contains several different elements; in category theory, we not only record the elements , also records the relationship between elements.
Martin Kuppe once drew a map of mathematics, putting category theory at the top of the map, shining on all fields of mathematics:
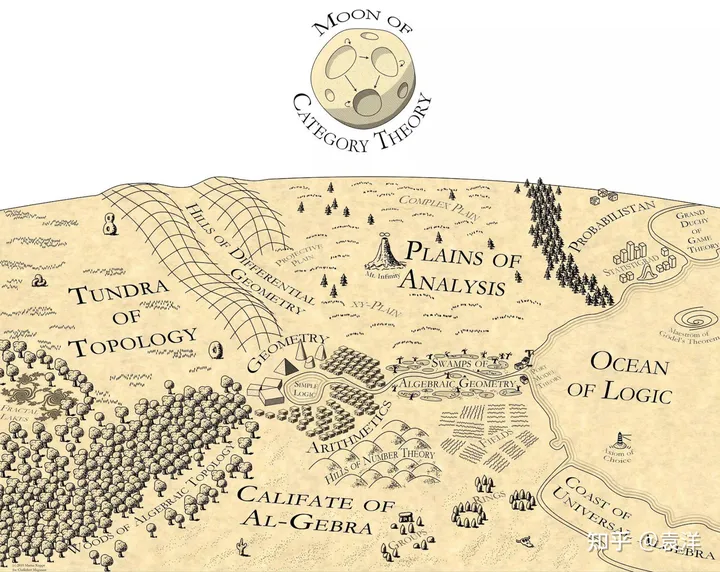
About category theory There are many introductions on the Internet. Let’s briefly talk about a few basic concepts here:

The category theory perspective of supervised learning

In the past ten years or so, people have conducted a lot of research around the supervised learning framework and obtained many beautiful conclusions. However, this framework also limits people's understanding of AI algorithms, making it extremely difficult to understand large pre-trained models. For example, existing generalization theories are difficult to explain the cross-modal learning capabilities of models.

Can we learn this functor by sampling its input and output data?
Notice that in this process we did not consider the internal structure of the two categories X and Y. In fact, supervised learning does not make any assumptions about the structure within the categories, so it can be considered that there is no relationship between any two objects within the two categories. Therefore, we can regard X and Y as two sets. At this time, the famous no free lunch theorem of generalization theory tells us that without additional assumptions, it is impossible to learn the functor from X to Y (unless there are massive samples).

At first glance, this new perspective is useless. Whether adding constraints to categories or adding constraints to functors, there seems to be no essential difference. In fact, the new perspective is more like a castrated version of the traditional framework: it does not even mention the concept of loss function, which is extremely important in supervised learning, and cannot be used to analyze the convergence or generalization properties of the training algorithm. So how should we understand this new perspective?
I think category theory provides a bird's-eye view. It does not by itself and should not replace the original more specific supervised learning framework, or be used to produce better supervised learning algorithms. Instead, supervised learning frameworks are its "sub-modules", tools that can be employed to solve specific problems. Therefore, category theory does not care about loss functions or optimization procedures - these are more like implementation details of the algorithm. It focuses more on the structure of categories and functors, and tries to understand whether a certain functor is learnable. These problems are extremely difficult in traditional supervised learning frameworks, but become simpler in the category perspective.
Category theory perspective of self-supervised learning
Pre-training tasks and categories

And these structures become the knowledge owned by the large model.
Specifically:
In other words, when we define the pre-training task on a data set, we define a category that contains the corresponding relationship structure. The learning goal of the pre-training task is to let the model learn this category well. Specifically, we look at the concept of an ideal model.
Ideal Model

Here, "data-agnostic" means is before seeing the data It is predefined; but the subscript f means that the two functions f and can be used through black box calls. In other words, is a "simple" function, but can draw on the capabilities of model f to represent more complex relationships. This may not be easy to understand. Let's use a compression algorithm as an analogy. The compression algorithm itself may be data-dependent, for example it may be specially optimized for the data distribution. However, as a data-independent function , it cannot access the data distribution, but it can call the compression algorithm to decompress the data, because the operation of "calling the compression algorithm" is data-independent.
For different pre-training tasks, we can define different :

Therefore, we can say: The process of pre-training learning is the process of finding the ideal model f.
However, even if is certain, by definition, the ideal model is not unique. Theoretically, model f could be super-intelligent and be able to do anything without learning the data in C. In this case, we cannot make a meaningful statement about the capabilities of f . Therefore, we should look at the other side of the problem:
Given a category C defined by a pre-trained task, for any ideal f , which tasks can it solve?
This is the core question we want to answer at the beginning of this article. Let us first introduce an important concept.
米田embed
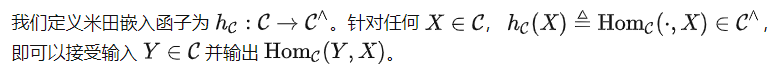

is ability The weakest ideal model, because given other ideal models f, all relations in are also contained in f. At the same time, it is also the ultimate goal of pre-training model learning without other additional assumptions. Therefore, to answer our core question, we consider below specifically .
Prompt tuning: Only by seeing a lot can you learn a lot

Yoneda Lemma

You can use these two representations to calculate T(X) . However, note that the quest prompt P must be sent via instead of , which means we will get (P) instead of T as input of. This leads to another important definition in category theory.
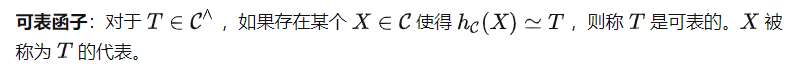
Theorem 1 and Corollary

Corollary 1. For the pre-training task of predicting image rotation angle [4], prompt tuning cannot solve complex downstream tasks such as segmentation or classification.
Proof: The pre-training task of predicting image rotation angles will rotate a given image by four different angles: 0°, 90°, 180°, and 270°, and let the model make predictions. Therefore, the categories defined by this pre-training task place each object into a group of 4 elements. Obviously, tasks like segmentation or classification cannot be represented by such simple objects.
Corollary 1 is a bit counter-intuitive, because the original paper mentioned [4] that the model obtained using this method can partially solve downstream tasks such as classification or segmentation. However, in our definition, solving the task means that the model should produce a correct output for every input, so being partially correct is not considered a success. This is also consistent with the question mentioned at the beginning of our article: With the support of unlimited resources, can the pre-trained task of predicting image rotation angles be used to solve complex downstream tasks? Corollary 1 gives a negative answer.
Fine tuning: representation without losing information
Tips that the ability to tune is limited, so what about the fine-tuning algorithm? Based on the Yoneda functor expansion theorem (see Proposition 2.7.1 in [5]), we can obtain the following theorem.
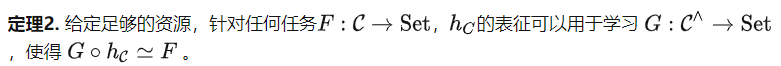
The downstream tasks considered in Theorem 2 are based on the structure of C, not the data content in the dataset. Therefore, the category defined by the previously mentioned pre-training task of predicting the angle of a rotated image still has a very simple group structure. But according to Theorem 2, we can use it to solve more diverse tasks. For example, we can map all objects to the same output, which is not possible with hint tuning. Theorem 2 clarifies the importance of pre-training tasks, since better pre-training tasks will create more powerful categories C, thus further improving the fine-tuning potential of the model.
There are two common misunderstandings about Theorem 2. First of all, even if category C contains a large amount of information, Theorem 2 only provides a rough upper bound, saying that records all the information in C and has the potential to solve any task, but it does not say that any fine-tuning algorithm can This purpose can be achieved. Second, Theorem 2 looks like an overparameterized theory at first glance. However, they analyze different steps of self-supervised learning. Parametric analysis is the pre-training step, which means that under certain assumptions, as long as the model is large enough and the learning rate is small enough, the optimization and generalization errors will be very small for the pre-training task. Theorem 2 analyzes the fine-tuning step after pre-training, saying that this step has great potential.
Discussion and summary
Supervised learning and self-supervised learning. From a machine learning perspective, self-supervised learning is still a type of supervised learning, but the way to obtain labels is more clever. But from a category theory perspective, self-supervised learning defines the structure within a category, while supervised learning defines the relationship between categories. Therefore, they are in different parts of the artificial intelligence map and are doing completely different things.

Applicable scene. Since the assumption of infinite resources was considered at the beginning of this article, many friends may think that these theories can only be truly established in the void. This is not the case. In our actual derivation process, we only considered the ideal model and the predefined function . In fact, as long as is determined, any pre-trained model f (even in the random initialization stage) can calculate f(X) for the input XC, and then use to calculate The relationship between two objects. In other words, as long as is determined, each pre-training model corresponds to a category, and the goal of pre-training is just to continuously align this category with the category defined by the pre-training task . Therefore, our theory holds for every pretrained model.
Core Formula. Many people say that if AI really has a set of theoretical support, then there should be one or several simple and beautiful formulas behind it. I think if a category theory formula needs to be used to describe the capabilities of large models, it should be what we mentioned before:
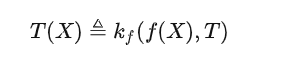
For those who are familiar with large models, After deeply understanding the meaning of this formula, you may feel that this formula is nonsense, but it is just a more complex mathematical formula to write out the working mode of the current large model.
but it is not the truth. Modern science is based on mathematics, and modern mathematics is based on category theory, and the most important theorem in category theory is Yoneda's lemma. The formula I wrote disassembles the isomorphism of Yoneda Lemma into an asymmetric version, but it is exactly the same as the way of opening the large model.
I think this must not be a coincidence. If category theory can illuminate various branches of modern mathematics, it can also illuminate the path forward for general artificial intelligence.
This article is inspired by the long-term and close cooperation with the Qianfang team of Beijing Zhiyuan Artificial Intelligence Research Institute.

Original link: https://mp.weixin.qq.com/s/bKf3JADjAveeJDjFzcDbkw
The above is the detailed content of Deep Thinking | Where is the capability boundary of large models?. For more information, please follow other related articles on the PHP Chinese website!

