What is the area of ​​an n-sided regular polygon of a given radius?

Here we will see how to calculate the area of ​​an n-sided regular polygon of a given radius. The radius here is the distance from any vertex to the center. To solve this problem, we draw a vertical line from the center to one of the sides. Assume the length of each side is 'a'. The perpendicular divides the side into two parts, each part having length a/2. A vertical line and a radius form an angle x. Suppose the length of the radius is h.

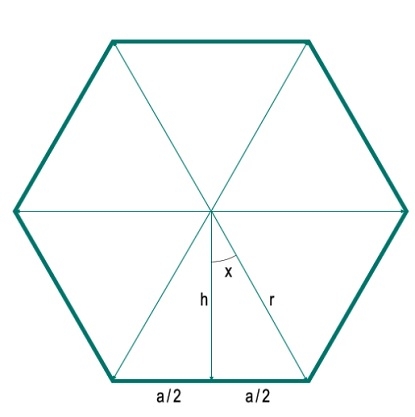
Here we can see that the polygon is divided into N equal triangles. Therefore, for any polygon with N sides, it will be divided into N triangles. Therefore, the angle at the center is 360 degrees. This is divided into 360°/N different angles (here 360°/6 = 60°). Therefore, the angle x is 180°/N. Now we can easily get h and a using trigonometric equations.

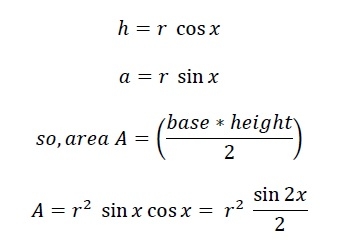
Now the area of ​​the entire polygon is N*A.

Example

#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
   return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
   angle to rad then calculate
}
int main() {
   float rad = 9.0f;
   int sides = 6;
   cout << "Polygon Area: " << polygonArea(rad, sides);
}

Output

Polygon Area: 210.44

The above is the detailed content of What is the area of ​​an n-sided regular polygon of a given radius?. For more information, please follow other related articles on the PHP Chinese website!