
In trees, the term "sum of the shortest paths of all pairs of nodes" refers to the calculation of the sum of the individual shortest paths of all pairs of nodes. An effective method is to use the dual DFS (depth first search) algorithm. The distance between the selected node and every other node is determined during the first DFS pass. The tree is traversed again during the second DFS pass, considering each node as a potential LCA (lowest common ancestor) and calculating the sum of distances between pairs of descendant nodes of the selected LCA. Using this method you can calculate the sum of the shortest paths for all pairs of nodes in the tree and ensure an ideal solution
usage instructions
Double DFS (depth first search) method
Dynamic programming method
Double DFS (depth first search) method
For the sum of all pairs of shortest paths in the tree, we use a dual DFS (depth-first search) method, which involves two DFS passes. First, we calculate the distance from any node to all other nodes. Then, during the second DFS traversal, we navigate the tree while considering each node as a potential LCA. We calculate and sum the distances between pairs of nodes that are descendants of the selected LCA while traversing. By repeating this process for all nodes, we obtain the sum of all pairs of shortest paths. This strategy is very compelling for this problem because it effectively computes the sum of distances between all sets of nodes in the tree.
algorithm
Any node in the tree can be used as the starting node
To determine the distance from the selected starting node to all other nodes, perform a depth-first search (DFS) starting from that node. These distances should be saved in an array or data structure.
Next, run a second depth-first search (DFS) on the tree, considering each node as its possible nearest common ancestor (LCA)
During the second DFS traversal of the tree, calculate the distance between pairs of nodes that are descendants of the selected LCA. For each LCA, these distances are added together.
Repeat this process for each node in the tree
The sum of all matches in the most limited way in the tree is represented by the sum of all calculated distances in step 4.
Example
is:Example
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
Output
Total sum of distances between descendants of the LCA: 0
Dynamic programming method:
We first select any node as the root node, and convert the tree into a rooted tree in the dynamic programming method, which is used to calculate the sum of the shortest paths between all nodes in the tree. We use dynamic programming to calculate the split between each node and the root node and store the results in an array. Then, for each node, we add the (computed) separations of its children from the root node to determine the overall separation of all other nodes. In this way, we can quickly calculate the total number of shortest paths between all nodes. As an efficient way to solve this problem, the time complexity of this algorithm is O(N), where N is the number of nodes in the tree.
algorithm
Take any node in the tree as the root and root the tree (for example, using a depth search of the root node) to create a rooted tree.
Dynamic programming can be used to determine the distance of each node from the root. These distances should be stored in an array or data structure.
Calculate the sum of the distances from each node to all other nodes in the tree:
The sum of all pairs of shortest paths in the tree is the final result.
a. Traverse the child nodes of the current node.
b. To consider the path through the current node, add the number of nodes in the subtree for each subtree and the distance to the root previously calculated for each subtree.
c. For each child node of the active node, add these amounts
d. Add the current node's total to the final result.
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
Output
Sum of all pair shortest paths in the tree: 0
in conclusion
The sum of all pairs of shortest paths in the tree can be calculated using the Double DFS (Depth First Search) method or dynamic programming. The Double DFS method consists of two passes, first calculating the distance from the selected node to all other nodes, and then traversing the tree again while treating each node as a potential lowest common ancestor (LCA) to sum the distances between Descendant node pairs. Dynamic programming methods require recursively using DFS to build the root of the tree and calculate the distance from the root to every other node. The result of both methods is the same and consists of the sum of all pairwise shortest paths in the tree. The decision between two algorithms may be based on specific implementation preferences or tree structures, but both algorithms provide efficient solutions.
The above is the detailed content of The sum of all pairs of shortest paths in the tree. For more information, please follow other related articles on the PHP Chinese website!
 树中所有对最短路径之和Aug 28, 2023 pm 03:17 PM
树中所有对最短路径之和Aug 28, 2023 pm 03:17 PM在树中,“所有节点对最短路径之和”的术语指的是计算所有节点对的个别最短路径的总和。一种有效的方法是使用双重DFS(深度优先搜索)算法。在第一次DFS遍历期间确定所选节点与每个其他节点之间的距离。在第二次DFS遍历期间再次遍历树,将每个节点视为潜在的LCA(最低公共祖先),并计算所选LCA的后代节点对之间的距离之和。使用这种方法可以计算出树中所有节点对最短路径之和,并确保得到一个理想的解决方案使用的方法双重DFS(深度优先搜索)方法动态规划方法双重DFS(深度优先搜索)方法对于树中所有对最短路径的
 如何使用java实现最短路径算法Sep 19, 2023 am 08:18 AM
如何使用java实现最短路径算法Sep 19, 2023 am 08:18 AM如何使用Java实现最短路径算法概述:最短路径算法是图论中一个重要的应用,在网络路由、地图导航等领域都有广泛的应用。在这篇文章中,我们将学习如何使用Java实现最短路径算法,并提供具体的代码示例。算法思路:最短路径算法有多种实现方式,其中最著名的两种算法是Dijkstra算法和A*算法。在这里我们将重点介绍Dijkstra算法的实现。Dijkstra算法的基
 深入探索Java中树和图的非线性数据结构应用和实现方法Dec 26, 2023 am 10:22 AM
深入探索Java中树和图的非线性数据结构应用和实现方法Dec 26, 2023 am 10:22 AM理解Java中的树和图:探索非线性数据结构的应用与实现引言在计算机科学中,数据结构是计算机中存储、组织和管理数据的方式。数据结构可以分为线性数据结构和非线性数据结构。树和图是非线性数据结构中最常用的两种类型。本文将重点介绍Java中树和图的概念、应用和实现,并给出具体的代码示例。树的概念与应用树是一种抽象数据类型,由节点和边组成的集合。树的每个节点包含一个数
 使用弗洛伊德-沃沙尔算法找到任意两个节点之间的最短路径Sep 20, 2023 pm 02:21 PM
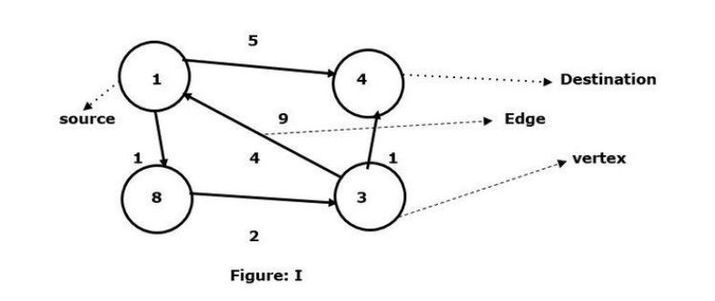
使用弗洛伊德-沃沙尔算法找到任意两个节点之间的最短路径Sep 20, 2023 pm 02:21 PMC++有一个宏,它被定义为一段代码或期望的值,并且每当用户需要时,它将被重复使用。弗洛伊德-沃尔夏尔算法是在给定的加权图中找到所有顶点对之间最短路径的过程。该算法遵循动态规划的方法来找到最小权重图。让我们通过图表来理解弗洛伊德-沃尔夏尔算法的含义-以顶点1为源,顶点4为目的地,求它们之间的最短路径。我们已经看到有两条路径可以连接到目标顶点4。1->4–边的权重为51->8->3->4–边权重(1+2+1)为4。在给定的图I中,我们看到两个顶点之间连接的最小边。所以这里顶点
 PHP算法设计思路:如何实现图的最短路径问题的高效解决方案?Sep 19, 2023 pm 03:43 PM
PHP算法设计思路:如何实现图的最短路径问题的高效解决方案?Sep 19, 2023 pm 03:43 PMPHP算法设计思路:如何实现图的最短路径问题的高效解决方案?在实际开发中,我们经常需要解决最短路径问题,例如在地图导航、网络路由、物流配送等领域。而图的最短路径算法是解决这类问题的关键。图由一组顶点和一组边组成。顶点表示节点,边表示节点之间的关系。最短路径问题就是找到连接两个节点的最短路径。在PHP中,我们可以使用多种算法来解决最短路径问题,其中最著名的算法
 递归在 C++ 数据结构中的妙用:栈和树的实现May 04, 2024 pm 01:54 PM
递归在 C++ 数据结构中的妙用:栈和树的实现May 04, 2024 pm 01:54 PM递归在C++数据结构中的应用:栈:通过后进先出(LIFO)结构递归实现栈。树:通过分层结构递归实现树,支持插入和深度计算等操作。递归为处理嵌套结构提供了简洁高效的解决方案,使数据结构的实现更加直观和易于维护。
 使用C++实现删除所有不在任何路径上且路径和小于k的节点Sep 04, 2023 am 10:17 AM
使用C++实现删除所有不在任何路径上且路径和小于k的节点Sep 04, 2023 am 10:17 AM在这个问题中,我们有一个二叉树,其从根节点到叶节点的路径是完全定义的。从根节点到叶子节点的所有节点之和必须大于或等于k。所以我们需要删除路径中总和小于k的所有节点。这里要记住的重要一点是,一个节点可能是许多路径的一部分,因此只有当所有路径的总和left的总和为10+20+5,即25,小于150,我们需要对其进行修剪并删除5。之后,让我们评估10->30->40。它小于150,所以删除40。现在我们看到另一条路径10->20->35->50,总和115小于150,所以
 C++程序以移除不满足路径和大于等于k的节点Sep 14, 2023 am 11:25 AM
C++程序以移除不满足路径和大于等于k的节点Sep 14, 2023 am 11:25 AM在这个问题中,我们有一个二叉树,其从根节点到叶节点的路径是完全定义的。从根节点到叶节点的所有节点的总和必须大于或等于常数值k。因此,我们需要删除那些总和小于k的路径中的所有节点,这样树中剩下的路径将大于k。这里要记住的重要一点是,一个节点可能是许多路径的一部分,因此只有当通向该节点的所有路径的总和left的总和为10+20+5,即25,小于150,我们需要对其进行修剪并删除5。之后,让我们评估10->30->40。它小于150,因此删除40。现在我们看到另一条路径10->20-


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

WebStorm Mac version
Useful JavaScript development tools

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver Mac version
Visual web development tools

Notepad++7.3.1
Easy-to-use and free code editor







