 Backend Development
Backend Development C++
C++ C++ program to calculate the logarithm of a given number based on a given base
C++ program to calculate the logarithm of a given number based on a given base
In almost all modern programming languages, we can find some logarithmic functions such as natural logarithm, base 2 logarithm, base 10 logarithm, etc. But sometimes we need to calculate logarithms of different bases that are not in the given library functions. To achieve this we can use a simple logarithmic formula. In this article, we will see how to calculate logarithmic value in C using a given number and a given base.
Formula for calculating logarithm given base
Suppose we have taken a number x, its base is k, which has also been given. The formula is as follows: The translation of follow −
is: follow −$$\mathrm{log_{k}\left ( x \right )=\frac{log_{m}\left ( x \right )}{log_{m}\left ( k \right )}}$ $
where m is any known (available base)
Use log10(), where m = 10.
C The cmath library provides the log10() method for finding the base 10 logarithm of a given number. us The same function can be used to calculate the logarithm of a given base k. The syntax used is: An example of log10() is as follows −
grammar
#include < cmath > Log10( <number> )
algorithm
Read two numbers x and k
res := (use log10(x) to find the base 10 logarithm of x) / (use log10(k) to find the base 10 logarithm of k)
return res
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( int x, int k){
float answer;
answer = log10( x ) / log10( k );
return answer;
}
int main(){
cout << "Log base 8 for input x = 512 is: " << solve( 512, 8 ) <<
endl;
cout << "Log base 9 for input x = 59049 is: " << solve( 59049, 9 )
<< endl;
cout << "Log base 2 for input x = 1024 is: " << solve( 1024, 2 ) <<
endl;
cout << "Log base 4 for input x = 256 is: " << solve( 256, 4 ) <<
endl;
}
Output
Log base 8 for input x = 512 is: 3 Log base 9 for input x = 59049 is: 5 Log base 2 for input x = 1024 is: 10 Log base 4 for input x = 256 is: 4
Use log2(), where m = 2.
In the cmath library of C, the log2() method allows users to find the logarithm with base 2 given number. The same function can be used to compute the logarithm of a specified base k The following syntax is used to use log2() −
grammar
#include < cmath > Log2( <number> )
algorithm
Read two numbers x and k
res := (use log2( x ) to find the base 2 logarithm of x) / (use log2( k ) to find the base 2 logarithm of x)
return res
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( int x, int k){
float answer;
answer = log2( x ) / log2( k );
return answer;
}
int main(){
cout << "Log base 8 for input x = 512 is: " << solve( 512, 8 ) <<
endl;
cout << "Log base 9 for input x = 59049 is: " << solve( 59049, 9 )
<< endl;
cout << "Log base 2 for input x = 1024 is: " << solve( 1024, 2 ) <<
endl;
cout << "Log base 4 for input x = 256 is: " << solve( 256, 4 ) <<
endl;
}
Output
Log base 8 for input x = 512 is: 3 Log base 9 for input x = 59049 is: 5 Log base 2 for input x = 1024 is: 10 Log base 4 for input x = 256 is: 4
Use log() when m=e.
In the C cmath library, the natural logarithm log() method allows the user to find the logarithm Use base 'e' for the given number. Logarithms can be calculated using a specified base k Same functionality. The following syntax is used to use the log() function −
grammar
#include < cmath > log( <number> )
algorithm
Read two numbers x and k
res := (use log(x) to find the logarithm of x with base e) / (use log(k) to find the logarithm of x with base e)
return res
Example
#include <iostream>
#include <cmath>
using namespace std;
float solve( int x, int k){
float answer;
answer = log( x ) / log( k );
return answer;
}
int main(){
cout << "Log base 8 for input x = 512 is: " << solve( 512, 8 ) <<
endl;
cout << "Log base 9 for input x = 59049 is: " << solve( 59049, 9 )
<< endl;
cout << "Log base 2 for input x = 1024 is: " << solve( 1024, 2 ) <<
endl;
cout << "Log base 4 for input x = 256 is: " << solve( 256, 4 ) <<
endl;
}
Output
Log base 8 for input x = 512 is: 3 Log base 9 for input x = 59049 is: 5 Log base 2 for input x = 1024 is: 10 Log base 4 for input x = 256 is: 4
in conclusion
Using the logarithmic formula of a given base can get the logarithmic result, We use any known base logarithm method on a given number x and divide it by The logarithmic base using a known value as the new base as input. In this article we use Three known existing logarithmic functions are log10(), log2() and log() [natural logarithm] Generates results for the given numbers and their given base.
The above is the detailed content of C++ program to calculate the logarithm of a given number based on a given base. For more information, please follow other related articles on the PHP Chinese website!
 新研究揭示量子蒙特卡洛超越神经网络在突破限制方面的潜力,Nature子刊详述最新进展Apr 24, 2023 pm 09:16 PM
新研究揭示量子蒙特卡洛超越神经网络在突破限制方面的潜力,Nature子刊详述最新进展Apr 24, 2023 pm 09:16 PM时隔四个月,ByteDanceResearch与北京大学物理学院陈基课题组又一合作工作登上国际顶级刊物NatureCommunications:论文《TowardsthegroundstateofmoleculesviadiffusionMonteCarloonneuralnetworks》将神经网络与扩散蒙特卡洛方法结合,大幅提升神经网络方法在量子化学相关任务上的计算精度、效率以及体系规模,成为最新SOTA。论文链接:https://www.nature.com
 MySQL中如何使用SUM函数计算某个字段的总和Jul 13, 2023 pm 10:12 PM
MySQL中如何使用SUM函数计算某个字段的总和Jul 13, 2023 pm 10:12 PMMySQL中如何使用SUM函数计算某个字段的总和在MySQL数据库中,SUM函数是一个非常有用的聚合函数,它可以用于计算某个字段的总和。本文将介绍如何在MySQL中使用SUM函数,并提供一些代码示例来帮助读者深入理解。首先,让我们看一个简单的示例。假设我们有一个名为"orders"的表,其中包含了顾客的订单信息。表结构如下:CREATETABLEorde
 计算矩阵右对角线元素之和的Python程序Aug 19, 2023 am 11:29 AM
计算矩阵右对角线元素之和的Python程序Aug 19, 2023 am 11:29 AM一种受欢迎的通用编程语言是Python。它被应用于各种行业,包括桌面应用程序、网页开发和机器学习。幸运的是,Python具有简单易懂的语法,适合初学者使用。在本文中,我们将使用Python来计算矩阵的右对角线之和。什么是矩阵?在数学中,我们使用一个矩形排列或矩阵,用于描述一个数学对象或其属性,它是一个包含数字、符号或表达式的矩形数组或表格,这些数字、符号或表达式按行和列排列。例如−234512367574因此,这是一个有3行4列的矩阵,表示为3*4矩阵。现在,矩阵中有两条对角线,即主对角线和次对
 Nature刊登量子计算重大进展:有史以来第一个量子集成电路实现Apr 08, 2023 pm 09:01 PM
Nature刊登量子计算重大进展:有史以来第一个量子集成电路实现Apr 08, 2023 pm 09:01 PM6 月 23 日,澳大利亚量子计算公司 SQC(Silicon Quantum Computing)宣布推出世界上第一个量子集成电路。这是一个包含经典计算机芯片上所有基本组件的电路,但体量是在量子尺度上。SQC 团队使用这种量子处理器准确地模拟了一个有机聚乙炔分子的量子态——最终证明了新量子系统建模技术的有效性。「这是一个重大突破,」SQC 创始人 Michelle Simmons 说道。由于原子之间可能存在大量相互作用,如今的经典计算机甚至难以模拟相对较小的分子。SQC 原子级电路技术的开发将
 面向长代码序列的 Transformer 模型优化方法,提升长代码场景性能Apr 29, 2023 am 08:34 AM
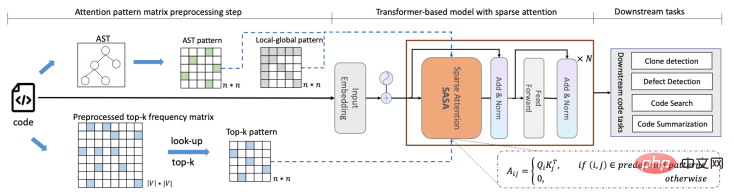
面向长代码序列的 Transformer 模型优化方法,提升长代码场景性能Apr 29, 2023 am 08:34 AM阿里云机器学习平台PAI与华东师范大学高明教授团队合作在SIGIR2022上发表了结构感知的稀疏注意力Transformer模型SASA,这是面向长代码序列的Transformer模型优化方法,致力于提升长代码场景下的效果和性能。由于self-attention模块的复杂度随序列长度呈次方增长,多数编程预训练语言模型(Programming-basedPretrainedLanguageModels,PPLM)采用序列截断的方式处理代码序列。SASA方法将self-attention的计算稀疏化
 Michael Bronstein从代数拓扑学取经,提出了一种新的图神经网络计算结构!Apr 09, 2023 pm 10:11 PM
Michael Bronstein从代数拓扑学取经,提出了一种新的图神经网络计算结构!Apr 09, 2023 pm 10:11 PM本文由Cristian Bodnar 和Fabrizio Frasca 合著,以 C. Bodnar 、F. Frasca 等人发表于2021 ICML《Weisfeiler and Lehman Go Topological: 信息传递简单网络》和2021 NeurIPS 《Weisfeiler and Lehman Go Cellular: CW 网络》论文为参考。本文仅是通过微分几何学和代数拓扑学的视角讨论图神经网络系列的部分内容。从计算机网络到大型强子对撞机中的粒子相互作用,图可以用来模
 清华大学类脑芯片天机芯X登Science子刊封面,机器人版猫捉老鼠上演Apr 14, 2023 pm 05:01 PM
清华大学类脑芯片天机芯X登Science子刊封面,机器人版猫捉老鼠上演Apr 14, 2023 pm 05:01 PM清华大学举办的一场机器人版猫捉老鼠游戏,登上了Science子刊封面。这里的汤姆猫有了新的名字:“天机猫”,它搭载了清华大学类脑芯片的最新研究成果——一款名为TianjicX的28nm神经形态计算芯片。它的任务是抓住一只随机奔跑的电子老鼠:在复杂的动态环境下,各种障碍被随机地、动态地放置在不同的位置,“天机猫”需要通过视觉识别、声音跟踪或两者结合的方式来追踪老鼠,然后在不与障碍物碰撞的情况下向老鼠移动,最终追上它。在此过程中,“天机猫”需要实现实时场景下的语音识别、声源定位、目标检测、避障和决
 使用math.Log2函数计算指定数字的以2为底的对数Jul 24, 2023 pm 12:14 PM
使用math.Log2函数计算指定数字的以2为底的对数Jul 24, 2023 pm 12:14 PM使用math.Log2函数计算指定数字的以2为底的对数在数学中,对数是一个重要的概念,它描述了一个数与另一个数(所谓的底)的指数关系。其中,以2为底的对数特别常见,并在计算机科学和信息技术领域中经常用到。在Python编程语言中,我们可以使用math库中的log2函数来计算一个数字的以2为底的对数。下面是一个简单的代码示例:importmathdef


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

SAP NetWeaver Server Adapter for Eclipse
Integrate Eclipse with SAP NetWeaver application server.

Atom editor mac version download
The most popular open source editor

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.






